To get started, there is an introduction with background and motivation, and an overview, summarizing the project as a whole.
Although Principia Cybernetica Web has received very positive reviews, the work is of course never finished. The material in this web is continuously being added to and improved. Nodes followed by the mention "[empty]" don't contain any text yet, only a menu of linked nodes. Some important results have not yet been converted to hypertext, but may be found in the papers in our FTP-archive.
Comments about content and presentation of the information are appreciated. If you have any technical problems, questions or suggestions on our Web, please contact the "Webmaster", Francis Heylighen (PCP@vub.ac.be). Comments about the content of a node can be addressed to its author(s). You can also directly annotate each node separately, or add general comments to the User Annotations.
We apologize for difficulties you might have in getting files from this server: Internet connections between Belgium and especially America are often overloaded. Try to avoid the most busy periods: 15.00 to 0.00 hrs (European time), i.e. 9.00 to 18.00 (US East Coast) or 6.00 to 15.00 (US West Coast), on weekdays. We would like to establish a mirror site in the US in order to avoid this problem in the future: proposals welcome! At present we only have a Belgian back-up FTP-server with WWW documents at ftp.vub.ac.be for emergencies, but it is not kept up-to-date. These servers are part of the network of the Free University of Brussels.
If you plan to regularly consult this server, you might keep a copy of this home page on your own computer.
Every time has its own approach to these eternal philosophical questions, deriving from its knowledge and technology. We hold that in our time, the age of information, it is systems science and cybernetics, as the general sciences of organization and communication, that can provide the basis for contemporary philosophy. Therefore, this philosophical system is derived from, and further develops, the basic principles of cybernetics.
Moreover, we start from the thesis that systems at all levels have been constructed by evolution, which we see as a continuing process of self-organization, based on variation and natural selection of the "fittest" configuration. Evolution continuously creates complexity and makes systems more adaptive by giving them better control over their environments. We consider the emergence of a new level of control as the quantum of evolution, and call it a "metasystem transition".
As cybernetic theory informs our philosophy, so cybernetic technology lets us do things that philosophers of other times could only dream of. Using computer technology, we develop a large philosophical text from many nodes which are linked together with different relationships. Readers can navigate among the many concepts, guided by their individual understanding and interests. Disparate material can be integrated together while being written and read by collaborators from all around the world, undergoing variation and selection. Thus we apply theories about the evolution of cybernetic systems to the practical development of this very system of philosophy.
We hold that PCP is more than an interesting experiment, and that there is an acute need for an approach similar to PCP. The on-going explosion and fragmentation of knowledge demands a renewed effort at integration. This has always been the dream of the systems theorists; all they lacked was the appropriate technology to attack the complexity of the task.
PCP draws its inspiration from many predecessors in intellectual history, including philosophers, systems scientists and cyberneticians, and others who have tried to collaboratively develop complex systems of thought.
This effort has been on-going since 1989, and is now in the stage of implementation (see our history). Of course, the task is enormous, and we are still beginning. If you are really interested in our Project, we invite you to join our efforts and become a contributor.
For further introductory reading, see the following documents:
The present document brings these different questions and answers together, in the form of a "FAQ" (Frequently Asked Questions). The answers given here are by necessity short. They barely scratch the surface of a profound and complex issue. However, where available, we have included links to other documents which discuss the problem in more detail. The present document can be seen as a roadmap, which will help philosophically interested readers to better explore the Principia Cybernetica world view.
We begin with the idea that philosophy is a kind of clear, deep thought; essentially putting our thought and language in order. This apparently analytic and linguistic understanding arises from the explicit recognition that all expression and communication, in particular all works of philosophy, the body of Principia Cybernetica, and this article itself, exist in a physical form as a series of symbol tokens in a particular modality and interpretable in a specific language and interpretational framework. It is impossible to consider philosophy in particular outside of the context of its processes and products. In that respect, philosophy must be understood as a process of philosophizing in which linguistic symbol tokens are produced and received. This includes the normal linguistic forms of speaking, hearing, reading, and writing, but also other linguistic forms such as diagrams, mathematics, and sign language. The authors of this paper philosophize as they write it; the readers philosophize as they read it. This article itself cannot have any existence "as philosophy" outside of this context of its production and/or reception.
What then distinguishes philosophical linguistic productions from any other? It is tempting to distinguish philosophy on the basis of its content, that is its referents, or what it is "about". Then we would believe, as some cybernetic philosophers have suggested \cite{BAA53a}, that philosophy is linguistic thought which refers to specific deep questions, e.g. about existence and knowledge, the nature of thought, and the ultimate good. We do not deny this, but do not believe that it is a good place to start in finding a definition.
Rather the focus on philosophizing as a process leads us to consider philosophy as any language conducted in a certain manner. In particular, whenever we deal with issues in depth, continually asking "why" and "how" to critically analyze underlying assumptions and move to the foundations of our complex knowledge structures, then that is necessarily philosophy. Thus we construct philosophy of language, of mind, or of law when we consider these specific subjects in their depth. Surely we could have a philosophy of plumbing or gum chewing should we wish.
As we proceed in the question asking mode towards deep thought and thus philosophy, then of course we are naturally drawn to the traditional philosophical questions outlined above. But what distinguishes them as the quintessential philosophical problems is their generality. Thus if we restrict ourselves specifically to (say) philosophy of law or plumbing, then perhaps we can avoid certain general philosophical issues. Philosophy per se is simply the result of philosophizing in an unrestricted domain of discourse.
See also: 
Cybernetics and Philosophy(paper by Turchin in tex format)
When we look at the history of epistemology, we can discern a clear trend, in spite of the confusion of many seemingly contradictory positions. The first theories of knowledge stressed its absolute, permanent character, whereas the later theories put the emphasis on its relativity or situation-dependence, its continuous development or evolution, and its active interference with the world and its subjects and objects. The whole trend moves from a static, passive view of knowledge towards a more and more adaptive and active one.
Let us start with the Greek philosophers. In Plato's view knowledge is merely an awareness of absolute, universal Ideas or Forms, existing independent of any subject trying to apprehend to them. Though Aristotle puts more emphasis on logical and empirical methods for gathering knowledge, he still accepts the view that such knowledge is an apprehension of necessary and universal principles. Following the Renaissance, two main epistemological positions dominated philosophy: empiricism, which sees knowledge as the product of sensory perception, and rationalism which sees it as the product of rational reflection.
The implementation of empiricism in the newly developed experimental sciences led to a view of knowledge which is still explicitly or implicity held by many people nowadays: the reflection-correspondence theory. According to this view knowledge results from a kind of mapping or reflection of external objects, through our sensory organs, possibly aided by different observation instruments, to our brain or mind. Though knowledge has no a priori existence, like in Plato's conception, but has to be developed by observation, it is still absolute, in the sense that any piece of proposed knowledge is supposed to either truly correspond to a part of external reality, or not. In that view, we may in practice never reach complete or absolute knowledge, but such knowledge is somehow conceivable as a limit of ever more precise reflections of reality.
The following important theory developed in that period is the Kantian synthesis of rationalism and empiricism. According to Kant, knowledge results from the organization of perceptual data on the basis of inborn cognitive structures, which he calls "categories". Categories include space, time, objects and causality. This epistemology does accept the subjectivity of basic concepts, like space and time, and the impossibility to reach purely objective representations of things-in-themselves. Yet the a priori categories are still static or given.
The next stage of development of epistemology may be called pragmatic. Parts of it can be found in early twentieth century approaches, such as logical positivism, conventionalism, and the "Copenhagen interpretation" of quantum mechanics. This philosophy still dominates most present work in cognitive science and artificial intelligence. According to pragmatic epistemology, knowledge consists of models that attempt to represent the environment in such a way as to maximally simplify problem-solving. It is assumed that no model can ever hope to capture all relevant information, and even if such a complete model would exist, it would be too complicated to use in any practical way. Therefore we must accept the parallel existence of different models, even though they may seem contradictory. The model which is to be chosen depends on the problems that are to be solved. The basic criterion is that the model should produce correct (or approximate) predictions (which may be tested) or problem-solutions, and be as simple as possible. Further questions about the "Ding an Sich" or ultimate reality behind the model are meaningless.
The pragmatic epistemology does not give a clear answer to the question where knowledge or models come from. There is an implicit assumption that models are built from parts of other models and empirical data on the basis of trial-and-error complemented with some heuristics or intuition. A more radical point of departure is offered by constructivism. It assumes that all knowledge is built up from scratch by the subject of knowledge. There are no 'givens', neither objective empirical data or facts, nor inborn categories or cognitive structures. The idea of a correspondence or reflection of external reality is rejected. Because of this lacking connection between models and the things they represent, the danger with constructivism is that it may lead to relativism, to the idea that any model constructed by a subject is as good as any other and that there is no way to distinguish adequate or 'true' knowledge from inadequate or 'false' knowledge.
We can distinguish two approaches trying to avoid such an 'absolute relativism'. The first may be called individual constructivism. It assumes that an individual attempts to reach coherence among the different pieces of knowledge. Constructions that are inconsistent with the bulk of other knowledge that the individual has will tend to be rejected. Constructions that succeed in integrating previously incoherent pieces of knowledge will be maintained. The second, to be called social constructivism, sees consensus between different subjects as the ultimate criterion to judge knowledge. 'Truth' or 'reality' will be accorded only to those constructions on which most people of a social group agree.
In these philosophies, knowledge is seen as largely independent of a hypothetical 'external reality' or environment. As the 'radical' constructivists Maturana and Varela argue, the nervous system of an organism cannot in any absolute way distinguish between a perception (caused by an external phenomenon) and a hallucination (a purely internal event). The only basic criterion is that different mental entities or processes within or between individuals should reach some kind of equilibrium.
Though these constructivistic approaches put much more emphasis on the changing and relative character of knowledge, they are still absolutist in the primacy they give to either social consensus or internal coherence, and their description of construction processes is quite vague and incomplete. A more broad or synthetic outlook is offered by different forms or evolutionary epistemology. Here it is assumed that knowledge is constructed by the subject or group of subjects in order to adapt to their environment in the broad sense. That construction is an on-going process at different levels, biological as well as psychological or social. Construction happens through blind variation of existing pieces of knowledge, and the selective retention of those new combinations that somehow contribute most to the survival and reproduction of the subject(s) within their given environment. Hence we see that the 'external world' again enters the picture, although no objective reflection or correspondence is assumed, only an equilibrium between the products of internal variation and different (internal or external) selection criteria. Any form of absolutism or permanence has disappeared in this approach, but knowledge is basically still a passive instrument developed by organisms in order to help them in their quest for survival.
A most recent, and perhaps most radical approach, extends this evolutionary view in order to make knowledge actively pursue goals of its own. This approach, which as yet has not had the time to develop a proper epistemology, may be called memetics. It notes that knowledge can be transmitted from one subject to another, and thereby loses its dependence on any single individual. A piece of knowledge that can be transmitted or replicated in such a way is called a 'meme'. The death of an individual carrying a certain meme now no longer implies the elimination of that piece of knowledge, as evolutionary epistemology would assume. As long as a meme spreads more quickly to new carriers, than that its carriers die, the meme will proliferate, even though the knowledge it induces in any individual carrier may be wholly inadequate and even dangerous to survival. In this view a piece of knowledge may be succesful (in the sense that it is common or has many carriers) even though its predictions may be totally wrong, as long as it is sufficiently 'convincing' to new carriers. Here we see a picture where even the subject of knowledge has lost his primacy, and knowledge becomes a force of its own with proper goals and ways of developing itself. That this is realistic can be illustrated by the many superstitions, fads, and irrational beliefs that have spread over the globe, sometimes with a frightening speed.
Like social constructivism, memetics attracts the attention to communication and social processes in the development of knowledge, but instead of seeing knowledge as constructed by the social system, it rather sees social systems as constructed by knowledge processes. Indeed, a social group can be defined by the fact that all its members share the same meme (Heylighen, 1992). Even the concept of 'self', that which distinguishes a person as a individual, can be considered as a piece of knowledge, constructed through social processes (HarrŽ, 19), and hence a result of memetic evolution. From a constructivist approach, where knowledge is constructed by individuals or society, we have moved to a memetic approach, which sees society and even individuality as byproducts constructed by an ongoing evolution of independent fragments of knowledge competing for domination.
We have come very far indeed from Plato's immutable and absolute Ideas, residing in an abstract realm far from concrete objects or subjects, or from the naive realism of the reflection-correspondence theory, where knowledge is merely an image of external objects and their relations. At this stage, the temptation would be strong to lapse into a purely anarchistic or relativistic attitude, stating that 'anything goes', and that it would be impossible to formulate any reliable and general criteria to distinguish 'good' or adequate pieces of knowledge from bad or inadequate ones. Yet in most practical situations, our intuition does help us to distinguish perceptions from dreams or hallucinations, and unreliable predictions ('I am going to win the lottery') from reliable ones ('The sun will come up tomorrow morning'). And an evolutionary theory still assumes a natural selection which can be understood to a certain degree. Hence we may assume that it is possible to identify selection criteria, but one of the lessons of this historical overview will be that we should avoid to quickly formulate one absolute criterion. Neither correspondence, nor coherence or consensus, and not even survivability, are sufficient to ground a theory of knowledge. At this stage we can only hope to find multiple, independent, and sometimes contradictory criteria, whose judgment may quickly become obsolete. Yet if we would succeed to formulate these criteria clearly, within a simple and general conceptual framework, we would have an epistemology that synthesizes and extends al of the traditional and less traditional philosophies above.
Such a theory would obviously be priceless for judging and constructing more specific physical theories. When we understand language as a hierarchical model of reality, i.e. a device which produces predictions, and not as a true static picture of the world, metaphysics is understood as much more valuable than just the "free fantasy" of philosophers. To say that the real nature of the world is a certain way means to propose the construction of a model of the world along those lines. Metaphysics creates a linguistic model (logical or conceptual structure) to serve as a basis for further refinements. Even though a mature physical theory fastidiously distinguishes itself from metaphysics by formalizing its basic notions and introducing verifiable criteria, metaphysics, in a very important sense, is physics.
Philosophies traditionally start with an ontology or metaphysics: a theory of being in itself, of the essence of things, of the fundamental principles of existence and reality. In a traditional systemic philosophy, "organization" might be seen as the fundamental principle of being, rather than God, matter, or the laws of nature. However this still begs the question of where this organization comes from. In a constructive systemic philosophy, on the other hand, the essence is the process through which this organization is created.
Alfred North Whitehead, Teilhard de
Chardin, Herbert Spencer, and Henry Bergson. Their main idea is to ground a philosophy on change or development, rather than on static concepts like matter or mind.
However, these early process philosophies are characterized by vagueness
and mysticism, and they tend to see evolution as teleological, goal
directed, guided by some supra-physical force, rather than as the blind
variation and selection process that we postulate. They are thus not
constructivist in the sense discussed in section constructivism. See further:
Australasian Association for Process Thought
Center
for Process Studies
Whitehead for dummies
Whitehead's even
more dangerous idea
Review of "L'Évolution Créatrice" by
Henri Bergson
Process Philosophy and the new thought movementDefinition according to Webster's Dictionary:
Recently, the term of "(formal) ontology" has been up taken by researchers in Artificial Intelligence, who use it to designate the building blocks out of which models of the world are made.(see e.g. "What is an ontology?"). An agent (e.g. an autonomous robot) using a particular model will only be able to perceive that part of the world that his ontology is able to represent. In a sense, only the things in his ontology can exist for that agent. In that way, an ontology becomes the basic level of a knowledge representation scheme. See for example my set of link types for a semantic network representation which is based on a set of "ontological" distinctions: changing-invariant, and general-specific.
What we need is a framework that ties everything together, that allows us to understand society, the world, and our place in it, and that could help us to make the critical decisions which will shape our future. It would synthesize the wisdom gathered in the different scientific disciplines, philosophies and religions. Rather than focusing on small sections of reality, it would provide us with a picture of the whole. In particular, it would help us to understand, and therefore cope with, complexity and change. Such a conceptual framework may be called a "world view".
The Belgian philosopher Leo Apostel has devoted his life to the development of such an integrating world view. As he quickly understood, the complexity of this task is too great for one man. Therefore, a major part of Apostel's efforts were directed at gathering other people, with different scientific and cultural backgrounds, to collaborate on this task. Only in the last years of his life, after several failed attempts, did he managed to create such an organization: the "Worldviews" group, which includes people from disciplines as diverse as engineering, psychiatry, theology, theoretical physics, sociology and biology.
Their first major product was a short book entitled "World views, from fragmentation to integration". This booklet is a call to arms, a program listing objectives rather than achievements. Its main contribution is a clear definition of what a world view is, and which are its necessary components. The "Worldviews" group has continued to work on different components and aspects of this general objective. Many of its members are also involved in a new interdisciplinary research center at the Free University of Brussels, which is named after Leo Apostel: the "Center Leo Apostel".
The book lists seven fundamental components of a world view. I will discuss them one by one, using a formulation which is slightly different from the one in the book, but which captures the main ideas.
Cybernetics and Systems Theory is an interdisciplinary academic domain. Although there are relatively few research centers and even fewer educational programs devoted to the domain, a lot of activity is going on in between established departments. This is shown by the number of associations, conferences and journals active in the domain.
The best way of getting acquainted with the main ideas of cybernetics and systems theory is to read a few of the classic books or papers defining the domain. Other, specific bibliographic references can be found in the library database of the Department of Medical Cybernetics and AI at the University of Vienna. There also exists more general reference material, including our own Web Dictionary of basic concepts.
You can get in touch with cybernetics and systems people via existing mailing lists and newsgroups, personal or departmental home pages, or by visiting conferences in the field (see the Calendar of events from the International Federation of Systems Research).
Systems theory or systems science argues that however complex or diverse the world that we experience, we will always find different types of organization in it, and such organization can be described by principles which are independent from the specific domain at which we are looking. Hence, if we would uncover those general laws, we would be able to analyse and solve problems in any domain, pertaining to any type of system. The systems approach distinguishes itself from the more traditional analytic approach by emphasizing the interactions and connectedness of the different components of a system.
Many of the concepts used by system scientists come from the closely related approach of cybernetics: information, control, feedback, communication... Cybernetics, deriving from the Greek word for steersman (kybernetes), was first introduced by the mathematician Wiener, as the science of communication and control in the animal and the machine (to which we now might add: in society and in individual human beings). It grew out of Shannon's information theory, which was designed to optimize the transmission of information through communication channels, and the feedback concept used in engineering control systems. In its present incarnation of "second-order cybernetics", its emphasis is on how observers construct models of the systems with which they interact (see constructivism).
In fact cybernetics and systems theory study essentially the same problem, that of organization independent of the substrate in which it is embodied. Insofar as it is meaningful to make a distinction between the two approaches, we might say that systems theory has focused more on the structure of systems and their models, whereas cybernetics has focused more on how systems function, that is to say how they control their actions, how they communicate with other systems or with their own components, ... Since structure and function of a system cannot be understood in separation, it is clear that cybernetics and systems theory should be viewed as two facets of a single approach.
This insight has had as a result that the two domains have in practice almost merged: many, if not most, of the central associations, journals and conferences in the field include both terms, "systems" and "cybernetics", in their title.
The following links should provide plenty of introductory material and references. An excellent, easy to read overview of the systems approach can be found in our web edition of the book "The Macroscope". Together with our dictionary, and list of basic books and papers, this should be sufficient for an introductory course in the domain:
Outside links:
Curriculum for Cybernetics and Systems Theory
review paper on cybernetics and its applications to social systems
General Systems Theory and Earth Science: an introduction to systems thinking
definition of Cybernetics in the Macmillan Encyclopedia of Computers
Systemic University on the Net (SUN): development and teaching of Systems Dynamics concepts
information on cybernetics from the ASC
ISSS project developing a primer on systems science
Educational Cybernetics: a course by Gary Boyd at Concordia University
description of an introductory course on Cybernetics and Systems Theory
course description on Systems Theory
a digest of systems theory, consisting of excerpts from basic books and papers
Systems Science Archives (mostly French) of the European Systems Union
| Synopsys: |
Systems theory was proposed in the 1940's by the biologist Ludwig von Bertalanffy (: General Systems Theory, 1968), and furthered by Ross Ashby (Introduction to Cybernetics, 1956). von Bertalanffy was both reacting agaInst reductionism and attempting to revive the unity of science. He emphasized that real systems are open to, and interact with, their environments, and that they can acquire qualitatively new properties through emergence, resulting in continual evolution. Rather than reducing an entity (e.g. the human body) to the properties of its parts or elements (e.g. organs or cells), systems theory focuses on the arrangement of and relations between the parts which connect them into a whole (cf. holism). This particular organization determines a system, which is independent of the concrete substance of the elements (e.g. particles, cells, transistors, people, etc). Thus, the same concepts and principles of organization underlie the different disciplines (physics, biology, technology, sociology, etc.), providing a basis for their unification. Systems concepts include: system-environment boundary, input, output, process, state, hierarchy, goal-directedness, and information.
The developments of systems theory are diverse (Klir, Facets of Systems Science, 1991), including conceptual foundations and philosophy (e.g. the philosophies of Bunge, Bahm and Laszlo); mathematical modeling and information theory (e.g. the work of Mesarovic and Klir); and practical applications. Mathematical systems theory arose from the development of isomorphies between the models of electrical circuits and other systems. Applications include engineering, computing, ecology, management, and family psychotherapy. Systems analysis, developed independently of systems theory, applies systems principles to aid a decisIon-maker with problems of identifying, reconstructing, optimizing, and controlling a system (usually a socio-technical organization), while taking into account multiple objectives, constraints and resources. It aims to specify possible courses of action, together with their risks, costs and benefits. Systems theory is closely connected to cybernetics, and also to system dynamics, which models changes in a network of coupled variables (e.g. the "world dynamics" models of Jay Forrester and the Club of Rome). Related ideas are used in the emerging "sciences of complexity", studying self-organization and heterogeneous networks of interacting actors, and associated domains such as far-from-equilibrium thermodynamics, chaotic dynamics, artificial life, artificial intelligence, neural networks, and computer modeling and simulation.
Francis Heylighen and Cliff Joslyn
Prepared for the Cambridge Dictionary of Philosophy.(Copyright Cambridge University Press)
de Rosnay The analytic and the systemic approaches are more complementary than opposed, yet neither one is reducible to the other.
The analytic approach seeks to reduce a system to its elementary elements in order to study in detail and understand the types of interaction that exist between them. By modifying one variable at a time, it tries to infer general laws that will enable one to predict the properties of a system under very different conditions. To make this prediction possible, the laws of the additivity of elementary properties must be invoked. This is the case in homogeneous systems, those composed of similar elements and having weak interactions among them. Here the laws of statistics readily apply, enabling one to understand the behavior of the multitude-of disorganized complexity.
The laws of the additivity of elementary properties do not apply in highly complex systems composed of a large diversity of elements linked together by strong interactions. These systems must be approached by new methods such as those which the systemic approach groups together. The purpose of the new methods is to consider a system in its totality, its complexity, and its own dynamics Through simulation one can "animate" a system and observe in real time the effects of the different kinds of interactions among its elements. The study of this behavior leads in time to the determination of rules that can modify the system or design other systems.
The following table compares, one by one, the traits of the two approaches.
| Analytic Approach | Systemic Approach |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Club of Rome) |
|
|
|
|
|
|
|
|
|
|
|
|
This table, while useful in its simplicity, is nevertheless a caricature of reality. The presentation is excessively dualist; it confines thought to an alternative from which it seems difficult to escape. Numerous other points of comparison deserve to be mentioned. Yet without being exhaustive the table has the advantage of effectively opposing the two complementary approaches, one of which-the analytic approach-has been favored disproportionately in our educational system.
Some recent fashionable approaches have their roots in ideas that were proposed by cyberneticians many decades ago: e.g. artificial intelligence, neural networks, complex systems, human-machine interfaces, self-organization theories, systems therapy, etc. Most of the fundamental concepts and questions of these approaches have already been formulated by cyberneticians such as Wiener, Ashby, von Bertalanffy \cite{V L56}, Boulding, von Foerster, von Neumann, McCulloch, and Pask in the 1940's through 1960's.
But since its founding, Cybernetics and Systems Science have struggled to find a degree of "respectability" in the academic community. While little interdisciplinary work has prospered recently, cyberneticians especially have failed to find homes in academic institutions, or to create their own. Very few academic programs in Cybernetics and Systems Science exist, and those working in the new disciplines described above seem to have forgotten their cybernetic predecessors.
What is the reason that cybernetics does not get the popularity it deserves? What distinguishes cyberneticians from researchers in the previously mentioned areas is that the former stubbornly stick to their objective of building general, domain independent theories, whereas the latter focus on very specific applications: expert systems, psychotherapy, thermodynamics, pattern recognition, etc. General integration remains too abstract, and is not sufficiently successful to be really appreciated.
As an interdisciplinary field, Cybernetics and Systems Science sees common concepts used in multiple traditional disciplines and attempts to achieve a consensual unification by finding common terms for similar concepts in these multiple disciplines. Thus sometimes Cybernetics and Systems Science abstracts away from concepts, theories, and terminologies in specific discipline towards general, and perhaps idiosyncratic, usages. These new conceptual categories may not be recognizable to the traditional researchers, or they may find no utility in the use of the general concepts.
Clearly the problem of building a global theory is much more complex than any of the more down-to-earth goals of the fashionable approaches. But we may also say that the generality of the approach is dangerous in itself if it leads to being "stuck" in abstractions which are so far removed from the everyday world that it is difficult to use them, interact with them, or test them on concrete problems; in other words, to get a feel for how they behave and what their strengths and weaknesses are.
Although there are many exceptions, researchers in Cybernetics and Systems Science tend to be trained in a traditional specialty (like biology, management, or psychology) and then come to apply themselves to problems in other areas, perhaps a single other area. Thus their exposure to Cybernetics and Systems Science concepts and theory tends to be somewhat ad hoc and specific to the two or three fields they apply themselves to.
Few have even attempted to address foundational theoretical and methodological issues in anything other than an ad hoc manner. Some conceptual "frameworks" exist at the formal, mathematical level \cite{KLG85c,MEMTA88}. Some researchers have presented integrated conceptual frameworks for major areas of systems science \cite{JAE80a,ODH83,POW73,TUV77}, and there have been some attempts to develop the foundations of the philosophy underlying cybernetics and systems theory \cite{BUM74,LAE72}. Yet these works focus specifically on cybernetics and systems theory from the perspectives of the traditional fields of mathematics or philosophy respectively; they are still locked into the traditional forms of development of academic work. There is as yet no systems theory of systems theories.
There is at the same time a lack of researchers who are willing or able to address themselves to the general problems and theories encompassed by cybernetics and systems theory. The lack of a coherent terminology and methodology is reflected in a lack of basic textbooks and glossaries, (with some exceptions \cite{ASR56,KLG91a,WEG75}) and further in a failure to establish even primary educational programs to instruct upcoming generations. What little interdisciplinary work has prospered has profited from the developments in cybernetics and systems theory over the past few decades while either ignoring or deliberately avoiding any reliance on cybernetics and systems theory (e.g. cite{SFI,WOS88}).
The lack of a strong foundation for or consensus within cybernetics and systems theory extends to the very basic information about the field. How do we describe ourselves, what can we tell new students and outsiders? Cybernetics and systems theory has been alternatively described as a science, a point of view, a world-view, an approach, an outlook, or a kind of applied philosophy or applied mathematics. There are those in our community who approve of and even champion this state of affairs. They focus on the creativity of the maverick academics who are drawn to cybernetics and systems theory, and decry any attempts to structure or build a solid theory.(Again, with some notable exceptions \cite{UMS90}.) Clearly this lack of balance has led to rather poor review standards in systems journals and conferences, and a low "signal to noise ratio".
What can account for the current state of affairs in cybernetics and systems theory, the lack of a consensually held fundamental theory? Is it inherent in the field, and necessary in any broad interdisciplinary studies? Or is it an historical accident, exacerbated by the personalities and careers of individual researchers? The Principia Cybernetica Project holds that there are in fact fundamental and foundational concepts, principles, and theories immanent in the body and literature of cybernetics and systems theory which do hold to general information systems, including all living and evolving systems at all levels of analysis. We contend that the lack of a fundamental theory is due to a lack of investment in the field. Support for and investment in a field are mutually reinforcing. A lack of either will lead to a lack of the other.
The domain of computing applications has grown so quickly that labeling anything that uses a computer as "cybernetic" is more obscuring than enlightening. Therefore we would restrict the label "cybernetic technology" to those information processing and transmitting tools that somehow increase the general purpose "intelligence" of the user, that is to say the control the user has over information and communication.
Especially all "value-added" computer-supported communication technologies (electronic mailing list, such as PRNCYB-L, newsgroups and bulletin boards, various forms of groupware, electronic publishing tools such as FTP or WWW) fall under this heading. They make it possible to exchange information in a very fast, simple and reliable way, so that it is automatically stored and ready for immediate further processing or transfer. The practical implication is that communication channels between far-away locations becomes so flexible and direct that they remind us of nerves, connecting and controlling different parts of an organism. The group of cooperators thus can behave more like a single system, with a vastly increased knowledge and intelligence, rather than like a collection of scattered individuals who now and then exchange limited messages, that need a lot of time to reach their destination and be processed.
In addition to communication, there is the aspect of increased control over information. The is especially obvious in computing tools that offer some kind of additional intelligence to the user: 1) everything deriving from artificial intelligence, and its daughter fields, such as expert systems, machine learning, and neural networks, where certain cognitive processes are automatized and thus taken over from the user; 2) the different tools that offer better ways to organize and represent information or knowledge, i.e. that support the user in building useful models. This category includes all types of computer simulation (e.g. virtual reality), knowledge representation tools, hypertext and multimedia, databases and information retrieval. The two features of computer intelligence and modelling are merged in what may be called "knowledge structuring": the use of computer programs that reorganize models in order to make them more adequate (more correct, simple, rich, easy-to-use, ...). (see a short paper by me, suggesting a possible way to introduce knowledge structuring in hypertexts)
The merging of the twin cybernetic dimensions of communication and control leads us to envision an all-encompassing, "intelligent" communication network, cyberspace, which may form the substrate for an emerging world-wide super-brain.
See also: Cybermedia
The word "cyberspace" was coined by the science fiction author William Gibson, when he sought a name to describe his vision of a global computer network, linking all people, machines and sources of information in the world, and through which one could move or "navigate" as through a virtual space.
The word "cyber", apparently referring to the science of cybernetics, was well-chosen for this purpose, as it derives from the Greek verb "Kubernao", which means "to steer" and which is the root of our present word "to govern". It connotes both the idea of navigation through a space of electronic data, and of control which is achieved by manipulating those data. For example, in one of his novels Gibson describes how someone, by entering cyberspace, could steer computer-controlled helicopters to a different target. Gibson's cyberspace is thus not a space of passive data, such as a library: its communication channels connect to the real world, and allow cyberspace navigators to interact with that world. The reference to cybernetics is important in a third respect: cybernetics defines itself as a science of information and communication, and cyberspace's substrate is precisely the joint network of all existing communication channels and information stores connecting people and machines.
The word "space", on the other hand, connotes several aspects. First, a space has a virtually infinite extension, including so many things that they can never be grasped all at once. This is a good description of the already existing collections of electronic data, on e.g. the Internet. Second, space connotes the idea of free movement, of being able to visit a variety of states or places. Third, a space has some kind of a geometry, implying concepts such as distance, direction and dimension.
The most direct implementation of the latter idea is the technology of virtual reality, where a continuous three-dimensional space is generated by computer, which reacts to the user's movements and manipulations like a real physical space would. In a more metaphorical way, the geometry (or at least topology) of space can be found in the network of links and references characterizing a hypertext (which can be seen as the most general form for a collection of interlinked data). Nodes in a hypertext can be close or distant, depending on the number of links one must traverse in order to get from the one to the other. Moreover, the set of links in a given node define a number of directions in which one can move. However, a hypertext does not seem to have any determined number of dimensions (except perhaps infinity), it is not continuous but "chunky", and the distance between two points is in general different depending on the point from which one starts to move.
One of the challenges for the researchers who are trying to make present computer networks look more like a Gibsonian cyberspace is to integrate the intuitive geometry of 3-D virtual reality, with the more general, but cognitively confusing, infinite dimensionality of hypertext nets (see e.g. NCSA's project on navigation through information space). A first step in that direction are the extensions to World-Wide Web which allow the user to do hypermedia navigation in a two-dimensional image (e.g. a map of Internet Resources), by associating clicks in different areas of the image with different hyperlinks. More ambitious proposals to develop a Virtual Reality interface to the World-Wide Web are being discussed.
As a description for what presently exists, the word "cyberspace" is used in a variety of significations, which each emphasize one or more of the meanings sketched above. Some use it as a synonym for virtual reality, others as a synonym for the World-Wide Web hypermedia network, or for the Internet as a whole (sometimes including the telephone, TV, and other communication networks).
None of the uses already seems to incorporate the most intrinsically cybernetic aspect of the concept: that of a shared medium through which one can exert control over one's environment. Control can apply as well to objects in cyberspace (e.g. when you alter the information in database through a Web form interface), as to objects in the real world (telepresence or teleoperation). As a first example of the control possibilities offered by the World-Wide Web, it is possible to steer a operated robot arm to do excavations. I would venture that it is that last dimension which will turn out to be the most important one in the future, as it may form the substrate for a cybernetic "superbeing" or "metabeing"...
See also:
definition of cyberspace in the Hacker's dictionary
Settling Cyberspace: the ethical frontier
It is therefore not surprising that the use of this same technology is the bedrock of practicing cyberneticians, and further holds the promise to resolve some of these conflicts between the objects and nature of cybernetic theory and the nature of academic work. In particular, it is now possible to develop representational media which share the characteristics of the systems being studied:
multiple orderings, and thus a nonlinear structure.
Traditional analytic methods tend to focus on individual, simple subsystems in isolation, while only occasionally (and frequently inaccurately) extrapolating to group traits. Temporal and physical levels of analysis are abstracted and isolated, and disciplinary divisions cut off consideration of their interaction.
This inadequacy is reflected in the actual products of academic and scientific work, the books, papers, and lectures which are the coin in trade for academic workers. Such works (like all traditional publications) have a linear structure, ranging from long treatises to collections of short paragraphs or sections (e.g. the work of Aristotle \cite{AR43} or Wittgenstein \cite{WIL58}). Various indexing and other methods are available to gain "random access" within documents. Dictionaries, encyclopedias, and other reference works partially introduce nonlinear structures through internal references (e.g. \cite{EDP67,KRK84,FLA79}). Some authors have made halting efforts in the direction of nonlinear documents \cite{MIM86}; others have used pictures and graphical notation to aid in understanding \cite{VOH81,ABRSHC85,VAF75,HAD88}. And certainly the use of formal systems (mathematics and logical notations) have given the ability to construct large, complex linguistic systems.
Nevertheless, over the years the fundamental linear textual form has been maintained. Works are produced by single or at most small groups of authors. Collaborative work among more than two people remains next to impossible. Work proceeds almost entirely in natural language. The development of large, complex systems of philosophical thought in non-formal domains has been difficult. Once published, the works sit on library shelves in mute inactivity. They are not even open to revision except through further publications and errata. The connections among and within works are revealed only through laborious reference searches and synthetic works by diligent authors. Tracing the historical development of ideas is as laborious as that of bibliographical relation. The physical form of texts required that the products of one author or the writings on one subject be physically scattered throughout a vast published literature, leading to a cacophonous din of argument and discourse.
The disciplinary divisions of academic work also place a regimented, linear, and highly specific structure to the categorization of published books and papers. Cybernetics and systems science researchers, on the other hand, typically utilize a great deal of the library shelves, including mathematics, all the traditional sciences, psychology and sociology, philosophy, linguistics, etc. In fact, ultimately there can be little doubt that cybernetics and systems science are not "academic disciplines" at all in the traditional sense of the word. As the trans- (inter-, meta-, anti-) disciplinary studies of general systems and information systems, cybernetics and systems science has long fought against the traditional disciplinary divisions of intellectual specialization.
This critique can be extended to the ultimate reflexivity of cybernetics and systems science, in which the academic milieu in which they operate is regarded as another cybernetic system, and therefore an object of study which itself should be understood through cybernetic principles.(Similarly, Turchin \cite{TUV77} describes the ultimate end of science as the reflexive study of the scientific process.)
Fe Institute),
and associated research in the natural sciences such as far-from-equilibrium thermodynamics, catastrophe theory, chaos and dynamical systems. A third strand are different high-level computing applications such as artificial intelligence, neural networks, man-machine interaction and computer
modeling and simulation. Unfortunately, few practitioners in these recent disciplines seem to be aware that many of their concepts and methods were proposed or used by cyberneticians since many years. Subjects like complexity, self-organization, connectionism and adaptive systems have already been extensively studied in the 1940's and 1950's, by researchers like Wiener, Ashby, von Neumann and von Foerster, and in discussion forums like the famous Josiah Macy meetings on cybernetics [Heims, 1991]. Some recent popularizing books on "the sciences of complexity" (e.g. Waldrop, 1992) seem to ignore this fact, creating the false impression that work on complex adaptive systems only started in earnest with the creation of the Santa Fe Institute in the 1980's.
Reference: S. Heims. The Cybernetics Group. MIT Press, Cambridge MA, 1991.
Santa Fe Institute is the gathering point for a new approach, which is usually presented as the study of "complex adaptive systems" (CAS). Whereas the authors in the "natural science" tradition are mostly European, while the cybernetics and systems researchers come from different continents, the CAS movement is predominantly American. Though it shares its subject, the general properties of complex systems across traditional disciplinary boundaries, with cybernetics and systems theory , the CAS approach is distinguished by the extensive use of computer simulations as a research tool, and an emphasis on systems, such as ecologies or markets, which are less integrated or "organized" than the ones, such as organisms, companies and machines, studied by the older tradition. Two popular science books, one by the science writer Mitchell Waldrop and one by the Nobel laureate and co-founder of the Santa Fe Institute Murray Gell-Mann, offer good reviews of the main ideas underlying the CAS approach. Another Santa Fe collaborator, the systems analyst John Casti, has written several popular science books, discussing different issues in the modelling of complex systems, while integrating insights from the CAS approach with the two older traditions.
John Holland is the founder of the domain of genetic algorithms. These are parallel, computational representations of the processes of variation, recombination and selection on the basis of fitness that underly most processes of evolution and adaptation (Holland, 1992). They have been successfully applied to general problem solving, control and optimization tasks, inductive learning (classifier systems, Holland et al., 1986), and the modelling of ecological systems (the ECHO model, Holland, 1996). The biologist Stuart Kauffman has tried to understand how networks of mutually activating or inhibiting genes can give rise to the differentiation of organs and tissues during embryological development. This led him to investigate the properties of Boolean networks of different sizes and degrees of connectedness. Through a reasoning reminiscent of Ashby, he proposes that the self-organization exhibited by such networks of genes or chemical reactions is an essential factor in evolution, complementary to Darwinian selection by the environment.
Holland's and Kauffman's work, together with Dawkins' simulations of evolution and Varela's models of autopoietic systems, provide essential inspiration for the new discipline of artificial life, This approach, initiated by Chris Langton (1989, 1992), tries to develop technological systems (computer programs and autonomous robots) that exhibit lifelike properties, such as reproduction, sexuality, swarming, and co-evolution. Tom Ray's Tierra program proposes perhaps the best example of a complex, evolving ecosystem, with different species of "predators", "parasites" and "prey", that exists only in a computer.
Backed by Kauffman's work on co-evolution, Wolfram's cellular automata studies, and Bak's investigations of self-organized criticality, Langton (1990) has proposed the general thesis that complex systems emerge and maintain on the edge of chaos, the narrow domain between frozen constancy and chaotic turbulence. The "edge of chaos" idea is another step towards an elusive general definition of complexity. Another widely cited attempt at a definition in computational terms was proposed by Charles Bennett.
Another investigation which has strongly influenced the artificial life community is Robert Axelrod's game theoretic simulation of the evolution of cooperation. By letting different strategies compete in a repeated Prisoner's Dilemma game, Axelrod (1984) showed that mutually cooperating, "tit-for-tat"-like strategies tend to dominate purely selfish ones in the long run. This transition from biological evolution to social exchanges naturally leads into the modelling of economic processes (Anderson, Arrow & Pines, 1988). W. Brian Arthur has systematically investigated self-reinforcing processes in the economy, where the traditional law of decreasing returns is replaced by a law of increasing returns, leading to the path-dependence and lock-in of contingent developments. More recently (1994), he has simulated the seemingly chaotic behavior of stock exchange-like systems by programming agents that are continuously trying to guess the future behavior of the system to which they belong, and use these predictions as basis for their actions. The conclusion is that the different predictive strategies cancel each other out, so that the long term behavior of the system becomes intrinsically unpredictable. This result leads back to von Foerster's second-order cybernetics, according to which models of social systems change the very systems they intend to model.
Bibliography: see the "classic publications on complex, evolving systems".
See also: Web servers on complexity and self-organization
The physicist Hermann Haken (1978) has suggested the label of synergetics for the field that studies the collective patterns emerging from many interacting components, as they are found in chemical reactions, crystal formations or lasers. Another Nobel laureate, Manfred Eigen (1992), has focused on the origin of life, the domain where chemical self-organization and biological evolution meet. He has introduced the concepts of hypercycle, an autocatalytic cycle of chemical reactions containing other cycles, and of quasispecies, the fuzzy distribution of genotypes characterizing a population of quickly mutating organisms or molecules (1979).
The modelling of non-linear systems in physics has led to the concept of chaos, a deterministic process characterized by extreme sensitivity to its initial conditions (Crutchfield, Farmer, Packard & Shaw, 1986). Although chaotic dynamics is not strictly a form of evolution, it is an important aspect of the behavior of complex systems. The science journalist James Gleick has written a popular history of, and introduction to, the field. Cellular automata, mathematical models of distributed dynamical processes characterized by a discrete space and time, have been widely used to study phenomena such as chaos, attractors and the analogy between dynamics and computation through computer simulation. Stephen Wolfram has made a fundamental classification of their types of behavior. Catastrophe theory proposes a mathematical classification of the critical behavior of continuous mappings. It was developed by René Thom (1975) in order to model the (continuous) development of (discontinuous) forms in organisms, thus extending the much older work by the biologist D' Arcy Thompson (1917).
Another French mathematician, Benoit Mandelbrot (1983), has founded the field of fractal geometry, which models the recurrence of similar patterns at different scales which characterizes most natural systems. Such self-similar structures exhibit power laws, like the famous Zipf's law governing the frequency of words. By studying processes such as avalanches and earthquakes, Per Bak (1988, 1991) has shown that many complex systems will spontaneously evolve to the critical edge between order (stability) and chaos, where the size of disturbances obeys a power law, large disturbances being less frequent than small ones. This phenomenon, which he called self-organized criticality, may also provide an explanation for the punctuated equilibrium dynamics seen in biological evolution.
Bibliography: see the "classic publications on complex, evolving systems".
See also: Web servers on complexity and self-organization
de Rosnay In illustrating a new current of thought, it is often useful to follow a thread. Our thread will be the Massachusetts Institute of Technology (MIT). In three steps, each of about ten years, MIT was to go from the birth of cybernetics to the most critical issue, the debate on limits to growth. Each of these advances was marked by many travels back and forth--typical of the systemic approach--between machine, man, and society. In the course of this circulation of ideas there occurred transfers of method and terminology that later fertilized unexplored territory.
In the forties the first step forward led from the machine to the living organism, transferring from one to the other the ideas of feedback and finality and opening the way for automation and computers. In the fifties it was the return from the living organism to the machine with the emergence of the important concepts of memory and pattern recognition, of adaptive phenomena and learning, and new advances in bionics (Bionics attempts to build electronic machines that imitate the functions of certain organs of living beings.): artificial intelligence and industrial robots. There was also a return from the machine to the living organism, which accelerated progress in neurology, perception, the mechanisms of vision In the sixties MIT saw the extension of cybernetics and system theory to industry, society, and ecology.
Three men can be regarded as the pioneers of these great breakthroughs: the mathematician Norbert Wiener, who died in 1964, the neurophysiologist Warren McCulloch, who died in 1969; and Jay Forrester, professor at the Sloan School of Management at MIT. There are of course other men, other research teams, other universities--in the United States as well as in the rest of the world--that have contributed to the advance of cybernetics and system theory. I will mention them whenever their course of research blends with that of the MIT teams.
In 1940 Wiener worked with a young engineer, Julian H. Bigelow, to develop automatic range finders for antiaircraft guns. Such servomechanisms are able to predict the trajectory of an airplane by taking into account the elements of past trajectories. During the course of their work Wiener and Bigelow were struck by two astonishing facts: the seem.ingly "intelligent" behavior of these machines and the "diseases" that could affect them. Theirs appeared to be "intelligent" behavior because they dealt with "experience" (the recording of past events) and predictions of the future. There was also a strange defect in performance: if one tried to reduce the friction, the system entered into a series of uncontrollable oscillations.
Impressed by this disease of the machine, Wiener asked Rosenblueth whether such behavior was found in man. The response was affirmative: in the event of certain injuries to the cerebellum, the patient cannot lift a glass of water to his mouth; the movements are amplified until the contents of the glass spill on the ground. From this Wiener inferred that in order to control a finalized action (an action with a purpose) the circulation of information needed for control must form "a closed loop allowing the evaluation of the effects of one's actions and the adaptation of future conduct based on past performances." This is typical of the guidance system of the antiaircraft gun, and it is equally characteristic of the nervous system when it orders the muscles to make a movement whose effects are then detected by the senses and fed back to the brain.
Thus Wiener and Bigelow discovered the closed loop of information necessary to correct any action--the negative feedback loop--and they generalised this discovery in terms of the human organism.
During this period the multidisciplinary teams of Rosenblueth were being formed and organized. Their purpose was to approach the study of living organisms from the viewpoint of a servomechanisms engineer and, conversely, to consider servomechanisms with the experience of the physiologist. An early seminar at the Institute for Advanced Study at Princeton in 1942 brought together mathematicians, physiologists, and mechanical and electrical engineers. In light of its success, a series of ten seminars was arranged by the Josiah Macy Foundation. One man working with Rosenblueth in getting these seminars under way was the neurophysiologist Warren McCulloch, who was to play a considerable role in the new field of cybernetics. In 1948 two basic publications marked an epoch already fertile with new ideas: Norbert Wiener's Cybernetics, or Control and Communication in the Animal and the Machine, and The Mathematical Theory of Communication by Claude Shannon and Warren Weaver. The latter work founded information theory.
The ideas of Wiener, Bigelow, and Rosenblueth caught fire like a trail of powder. Other groups were formed in the United States and around the world, notably the Society for General Systems Research whose publications deal with disciplines far removed from engineering such as sociology, political science, and psychiatry.
The seminars of the Josiah Macy Foundation continued, opening to new disciplines: anthropology with Margaret Mead, economics with Oskar Morgenstern. Mead urged Wiener to extend his ideas to society as a whole. Above all, the period was marked by the profound influence of Warren McCulloch, director of the Neuropsychiatric Institute at the University of Illinois.
At the conclusion of the work of his group on the organization of the cortex of the brain, and especially after his discussions with Walter Pitts, a brilliant, twenty-two-year-old mathematician, McCulloch understood that a beginning of the comprehension of cerebral mechanisms (and their simulation by machines) could come about only through the cooperation of many disciplines. McCulloch himself moved from neurophysiology to mathematics, from mathematics to engineering.
Walter Pitts became one of Wiener's disciples and contributed to the exchange of ideas between Wiener and McCulloch; it was he who succeeded in convincing McCulloch to install himself at MIT in 1952 with his entire team of physiologists.
Paralleling the work of the teams of Wiener and McCulloch at MIT, another group tried to utilize cybernetics on a wider scope. This was the Society for General Systems Research, created in 1954 and led by the biologist Ludwig von Bertalanffy. Many researchers were to join him: the mathematician A. Rapoport, the biologist W. Ross Ashby, the biophysicist N. Rashevsky, the economist K. Boulding. IIn 1954 the General Systems Yearbooks began to appear; their influence was to be profound on all those who sought to expand the cybernetic approach to social systems and the industrial firm in particular.
During the fifties a tool was developed and perfected that would permit organized complexity to be approached from a totally new angle--the computer. The first ones were ENIAC (1946) and EDVAC or EDSAC (1947). One of the fastest was Whirlwind 11, constructed at MIT in 1951. It used--for the first time--a superfast magnetic memory invented by a young electronics engineer from the servomechanisms laboratory, Jay W. Forrester.
As head of the Lincoln Laboratory, Forrester was assigned by the Air Force in 1952 to coordinate the implementation of an alert and defense system, the SAGE system, using radar and computers for the first time. Its mission was to detect and prevent possible attack on American territory by enemy rockets. Forrester realized the importance of the systemic approach in the conception and control of complex organizations involving men and machines in "real time": the machines had to be capable of making vital decisions as the information arrived.
In 1961, having become a professor at the Sloan School of Management at MIT, Forrester created Industrial Dynamics. His object was to regard all industries as cybernetics systems in order to simulate and to try to predict their behavior.
In 1964, confronted with the problems of the growth and decay of cities, he
extended the industrial dynamics concept to urban systems (Urban Dynamics).
Finally, in 1971, he generalized his earlier works by creating a new
discipline, system dynamics, and published World Dynamics. This book was
the basis of the work of Dennis H. Meadows and his team on the limits to
growth. Financed by the Club of Rome these works were to have worldwide impact
under the name MIT Report
See also: the origin of cybernetics and the biographies of the most important cybernetic thinkers at the cybernetics page of the ASC
This list was provided as a special service to our readers, since we noticed that the names of these people were among the most common strings entered in our search engine. Therefore, the list is directly searchable through the PCP title search. The [Search PCP] link after each name will find all references to the name in other Principia Cybernetica Web pages, while [find books] will give you a list of books by or on the author, available through the Amazon web bookshop.
Shalizi's notes - [Search PCP]- [Find Books]
home page - biography (French) - [Search PCP]- [Find Books]
biography - ASC biography - the Tangled Web - Ecology of Mind page - [Search PCP] - [Find Books]
ASC biography - ISSS primer - ISSS luminaries - Team Syntegrity biography - [Search PCP]- [Find Books]
ASC biography - ideas and works - dedication - [Search PCP] - [Find Books]
home page - Profile - Soft Systems Methodology - [Search PCP] - [Find Books]
Home page - ASC biography - short bio - [Search PCP] - [Find Books]
home page - [Search PCP] - [Find Books]
bibliography - [Search PCP] - [Find Books]
ASC biography - photo - contribution to psychology and complexity theory - biology of cognition - Ecology of Mind page - short bio - The Observer Web: autopoiesis theory - [Search PCP] - [Find Books]
ASC biography - McCulloch and Pitts neurons - von Foerster's tribute - [Search PCP] - [Find Books]
intro to Miller's LST - Miller on "The Earth as a System" - Applications of LST - [Search PCP] - [Find Books]
biography - summary - interview - bibliography - [Search PCP] - [Find Books]
biography - [Search PCP] - [Find Books]
Pangaro's archive - In Memoriam - ISSS luminaries - ASC biography - [Search PCP] - [Find Books]
home page - [Search PCP] - [Find Books]
home page - introduction to perceptual control theory - definition of control - [Search PCP] - [Find Books]
bibliography - [Search PCP] - [Find Books]
biography - biography 2 - History of mathematics biography - biography4 - a personal biography - biography and achievements - Shannon's information theory - photos - [Search PCP] - [Find Books]
biography - The Observer Web: autopoiesis theory - [Search PCP] - [Find Books]
biography - [Search PCP] - [Find Books]
biography & contact info - [Search PCP] - [Find Books]
overview - biographical interview - Varela's personal introduction - [Search PCP] - [Find Books]
biography - bio with bibliography -History of mathematics biography - biography3 - biography4 - [Search PCP] - [Find Books]
ASC biography - [Search PCP] - [Find Books]
ideas - biography - Shalizi's notes - Notices of the AMS bio - bio (mathematicians) - MathematicalWork - his Cybernetic Delirium - his activism - in K. Kelly's "Out of Control" - memoir - [Search PCP] - [Find Books]Great Thinkers & VisionariesBiographies of scientistsKey Contributors to Cybernetics (ASC)Biographies of mathematiciansJoël de Rosnay. It was originally published in
1979 by Harper & Row, (New York), but is now out of print. Therefore, we have made it again available on the web.
Dr. Joël de Rosnay, a molecular biologist, systems theorist, science writer,
and futurologist, is presently Director of Strategy of the Cite des
Sciences et de l'Industrie at La Villette (near Paris). He is an associate
of the Principia Cybernetica Project.
This book is an excellent, easy to read introduction to cybernetics and systems thinking, with applications to living organisms, the economy and the world as a whole. The main theme is that the complex systems which govern our life should be looked at as a whole, rather than be taken apart into their constituents. The different systems, processes and mechanisms are beautifully illustrated with examples and pictures. Although the text is over 20 years old, this visionary document is still highly relevant to our present situation and state of knowledge. It is particularly recommended to people who wish to get an understanding of the basic concepts and applications of systems theory and cybernetics. The chapters below can be read independently of each other.
Other, specific bibliographic references of books and a selected number of papers can be found in the library database of the Department of Medical Cybernetics and AI at the University of Vienna. A number of more recent books and papers can be found in our bibliography on the complex, evolving systems.
The books with links below can be securely ordered and paid for over the web from Amazon.com, the largest bookstore on the Net.
Key: ** Required
* Recommended
Excellent graphical introduction to dynamic systems theory.
Ackoff, Russel: (1972) On Purposeful Systems, Aldine Press, Chicago
Grand philosophy of human systems as teleological, goal-seeking. Structure, function, and purpose. Cognitive models and action in psychology; linguistics and semantics; conflict and cooperation; social systems.
Alan, TFH, and Starr, TB: (1982) Hierarchy: Perspective for Explaining Ecological Complexity, U. Chicago, Chicago
Anderson, PW, and Arrow, KJ et. al.: eds. (1988) Economy as an Evolving, Complex System, Addison-Wesley, New York
Critical anthology of system economic theory: applied mathematical techniques, dynamical theory, bounded rationality. Kauffman on "web searching"; Holland; Ruelle on nonlinear dynamics; Baum on neural nets.
Angyal, A: (1969) Logic of Systems, Penguin
Arbib, Michael A: (1972) Metaphorical Brain, Wiley, New York,
* Ashby, Ross: (1952) Design for a Brain, Wiley, New York.
A classic book, introducing fundamental systems concepts with examples related to the brain.
** (1956) Introduction to Cybernetics, Methuen, London
** (1981) Mechanisms of Intelligence: Writings of Ross Ashby/, ..... ed. Roger Conant
Atkin, RH: (1976) Mathematical Structure in Human Affairs, Heineman, London
Introduces Q-analysis, a methodology for identifying structures in data. The methodology uses some ideas of differential geometry.
Auger, Peter: (1990) Dynamics and Thermodynamics in Hier. Organized Sys., to appear
Aulin, AV: (1989) Foundations of Mathematical System Dynamics, Pergamon, Oxford
Causal recursion and its application to social science and economics, fundamental dynamics, self-steering, self-regulation, origins of life and mind.
* Aulin, AY: (1982) Cybernetic Laws of Social Progress, Pergamon, Oxford
Cybernetic social theory, including the Law of Requisite Hierarchy.
..... (1989) Foundations of Mathematical Systems Dynamics, Pergamon Press, Oxford
Barnsley, MF: (1988) Fractals Everywhere, Academic Press, San Diego
Best text on fractal geometry.
** Bateson, Gregory: (1972) Steps to an Ecology of Mind, Ballantine, New York
Bateson's critical essays. For purchase.
..... (1979) Mind and Nature, Bantam, New York
Unlike _Steps to an Ecology of Mind_, _Mind and Nature_ is an attempt at a coherent, popular statement of Bateson's philosophy.
Bayraktar, BA, and et. al., : eds. (1979) Education in Systems Science, Taylor and Francis, London
* Beer, Stafford: (1975) Platform for Change, Wiley, London
Foundational work in management cybernetics.
Bellman, Richard: (1972) Adaptive Control Processes: A Guided Tour, Princeton U, Princeton
An excellent book covering fundamental concept of systems science.
Beltrami, Edward: (1987) Mathematics for Dynamic Modeling, Academic Press, Orlando
Excellent mathematical introduction to dynamic systems theory, including catastrophe theory. Key results and theorems, examples. Many typos.
Blalock, HM: (1969) Systems Theory: From Verbal to Mathematical Formulation, Prentice Hall, Eng.Cliffs NJ
* Blauberg, IV, and Sadovsky, VN: (1977) Systems Theory: Philosophy and Methodological Problems, Progress, Moscow
One of the best overviews of philosphical and methodological development in systems theory, both in the Soviet Union and in the West.
Bogdanov, A.: (1980) Essays in Tektology, Intersystems
Translation of historical foundation of systems science.
Booth, TL: (1967) Sequential Machines and Automata Theory, Wiley, New York
One of the most comprehensive books on finite state machines, both deterministic and probablistic.
* Boulding, Ken: (1978) Ecodynamics, Sage, Beverly Hills
Unified theory of economics and social systems theory in terms of communicative processes.
..... (1985) World as a Total System, Sage, Beverley Hills
Brillouin, Leon: (1964) Scientific Uncertainty and Information, Academic Press, New York
Classic work on the relation between thermodynamics, information theory, and the necessary conditions for observability.
Brooks, DR, and Wiley, EO: (1988) Evolution as Entropy, 2nd edition, U. of Chicago, Chicago
Recent treatise on entropy as a general measure for biological study. Definitions of non-thermodynamic, non-informational entropies at multiple levels of analysis. Severely criticized.
Brown, G. Spencer: (1972) Laws of Form, Julian Press, New York
Philosophy of and notational system for propositional logic.
Basis for a whole school of graphical approaches to classical logic.
Brunner, RD, and Brewer, GD: (1971) Organized Complexity, Free Press, New York
Buckley, W: ed. (1968) Modern Systems Research for the Behavioral Scientist, Aldine, Chicago
Bunge, Mario: Method, Model, and Matter, D. Reydel
Campbell, Jeremy: (1982) Grammatical Man, Simon and Schuster, New York
Popular treatment of many aspects of cognitive science, information theory, and linguistics.
Cariani, Peter A: (1989) On the Design of Devices w/Emergent Semantic Functions, SUNY-Binghamton, Binghamton NY, NOTE: PhD Dissertation
Casti, John: (1979) Connectivity, Complexity and Catastrophe in Large-Scale Systems, J. Wiley, New York
..... * (1989) Alternate Realities: Mathematical Models of Nature and Man, Wiley, New York
Modern and very comprehensive text on mathematical modeling.
* Cavallo, Roger E: (1979) Role of Systems Methodology in Social Science Research, Martinus Nijhoff, Boston
Introduces the GSPS framework and discusses how it can be utilizes in social science research.
* Checkland, Peter: (1981) Systems Thinking, Systems Practice, Wiley, New York
Foundations of an area called soft systems methodology, for social systems management.
Christensen, Ronald: (1980) Entropy Minimax Sourcebook, Entropy Limited, Lincoln, MA, NOTE: Four volumes
..... (1983) Multivariate Statistical Modeling, Entropy Limited, Lincoln MA
Churchman, CW: (1968) Systems Approach, Delta, New York
General introduction to systems thinking in management.
..... (1971) Design of Inquiring Systems, Basic Books, New York
..... (1979) Systems Approach and its Enemies, Basic Books, New York,
Social systems philosophy. But also really about logic and mathematical description, excluded middles as "enemies"; relation of epistemics to action. Lucid, entertaining, critical.
Clemson, Barry: (1984) Cybernetics: A New Management Tool, Abacus Press, Kent
Guide to the theory and practice of management cybernetics. Based on Beer.
Codd, EF: (1968) Cellular Automata, Academic Press, New York,
Csanyi, V: (1982) General Theory of Evolution, Akademia Kiado, Budapest
On universal evolution. Ambitious, non-technical discussion.
Davies, Paul: (1988) Cosmic Blueprint, Simon and Schuster, New York
Excellent popular survey of complex systems theory.
De Chardin, Teilhard: (1959) The Phenomenon of Man, Harper and Row, New York
Early systemic evolutionary theology.
Denbigh, Kenneth G: (1975) An Inventive Universe, Hutchinson, London
On emergence and thermodynamics.
Denbigh, Kenneth G, and Denbigh, JS: (1985) Entropy in Relation to Incomplete Knowledge, Cambridge U., Cambridge
Good survey of quantum statistical dynamics, objectivity and subjecticity, basis of the fundamental assumption of thermodynamics, resolution of Gibbs paradox, relation to information theory.
Distefano, JJ, and et. al., : (1967) Feedback and Control Systems, Schaum, New York
Dretske, Fred: (1982) Knowledge and the Flow of Information, MIT Press, Cambridge
Treatise on information theory, syntax, and semantic.
Edelman, G: (1987) Neural Darwinism, Basic Books, New York
Theory of selectional processes at the neural level.
Eigen, M, and Schuster, P: (1979) The Hypercycle, Springer-Verlag, Heidelberg
Now classic work on the autocatalysis in chemical cycles: the cybernetic basis of metabolism.
Eigen, M, and R. Oswatitsch (1996): Steps Toward Life: a perspective on evolution
Erickson, Gary J: ed. (1988) Maximum-Entropy and Bayesian Methods in Science and Engineering, v. 1,2, Kluwer
Proceedings of the 5th, 6th, and 7th MaxEnt workshops. Foundations and applications. Spectral analysis, inductive reasoning, uncertainty and measurement, information theory in biology, etc.
Farlow, SJ: (1984) Self-Organizing Methods in Modeling, Marcel Dekker, New York
Feistel, Rainer, and Ebeling, Werner: (1988) Evolution of Complex Systems, Kluwer, New York
Oscillation and chaos in mechanical, electrical, chemical, and biological systems. Thermodynamics and spatial structures. Sequences, information, and language. Self-reproducgin systems, Lotka-Volterra systems.
Forrester, JW: (1961) Industrial Dynamics, MIT Press, Cambridge
..... (1971) World Dynamics, Wright and Allen, Cambridge
Influential early attempt at modeling the "world problem": the global economic-ecological web. Like the 's _Limits to Growth_.
..... * ed. (1975) Collected Papers of Jay W. Forrester, Wright-Allen, Cambridge
Papers by the outher of the "DYNAMO" differential systems tool, used for global ecological modeling.
Garey, MR, and Johnson, DS: (1979) Computers and Intractability: Guide to NP-Completeness, WH Freeman, San Francisco
One of the best monographs on computational complexity, NP-completeness and hardness, etc.
Gatlin, L: (1972) Information Theory and the Living System, Columbia U., New York
Classic work on the use of information theory in the analysis of genetic structure, evolution, and general biology.
* Gleick, James: (1987) Chaos: Making of a New Science, Viking, New York
Solid popular introduction to chaotic dynamics and fractal theory.
Glushkov, VM: (1966) Introduction to Cybernetics, Academic Press, New York
Excellent book on cybernetics, translated from Russian.
Greeniewski, H: Cybernetics Without Mathematics, Pergamon, Oxford
Gukhman, AA: (1965) Introduction to the Theory of Similarity, Acadenmic Press, New York
One of the excellent books on the theory of similarity.
* Haken, Herman: (1978) Synergetics, Springer-Verlag, Heidelberg
Original work by this unique developer of a "competitor" to systems science as the study of natural complex systems.
..... (1988) Information and Self-Organization, Springer-Verlag, New York
On synergetics as the science of complex systems. Integrates information theory, bifurcation theory, maximum entropy theory, and semantics.
Hall, AD: (1989) Metasystems Methodology, Pergamon, Oxford
Halme, A, and et. al., : eds. (1979) Topics in Systems Theory, Acta Polytechnica, Scandanavia
Hammer, PC: ed. (1969) Advances in Mathematical Systems Theory, Penn St. U, U. Park, PA
Hanken, AFG, and Reuver, HA: (1981) Social Systems and Learning Systems, Martinus Nijhoff, Boston
Happ, HH: ed. (1973) Gabriel Kron and Systems Theory, Union College Press, Schenectady NY
Hartnett, WE: ed. (1977) Systems: Approaches, Theories, Applications, Reidel, Boston
Herman, GT, and Rozenberg, G: (1975) Developmental Systems and Languages, North-Holland, New York
* Holland, John: (1976) Adaptation in Natural and Artificial Systems, U. Michigan, Ann Arbor
On the genetic algorithms method of modeling adaptive systems.
..... Hidden Order : How Adaptation Builds Complexity
..... Induction : Processes of Inference, Learning and Discovery;
Kanerva, Penti: (1988) Sparse Distributed Memory, MIT Press, Cambridge
On the geometry of high dimensional, low cardinality spaces; application to associative memory.
Klir, George: (1969) An Approach to General Systems Theory, van Nostrand, New York
An early book that describes the nucleus of what is known now as the General Systems Problem Solver.
..... ed. (1972) Trends in General Systems Theory, Wiley, New York
Contains overviews of systems conceptual frameworks of Mesarovic, Wymore, and Klir; and other papers on some fundamental issues of systems science.
..... ed. (1981) Special Issue on Reconstructibility Analysis, in: Int. J. Gen. Sys., v. 7:1, pp. 1-107
Broekstra, Cavallo, Conant, Klir, Krippendorff
..... (1985) Architecture of Systems Problem Solving, Plenum, New York
Vast, general theory of epistemological systems, outline of a platform for general systems modeling and inductive inference.
..... **(1992) Facets of Systems Science, Plenum, New York
Reprints of most classical papers in systems science with an up-to-date introduction. Recommended for everyone as a general introduction to the domain
Klir, George, and Folger, Tina: (1987) Fuzzy Sets, Uncertainty, and Information, Prentice Hall
Primary text on fuzzy systems theory and extended information theory.
Koestler, Arthur, and Smythes, J.R.: eds. (1968) Beyond Reductionism, Hutchinson, London
Classical anthology on holism and reductionism.
Krinsky, VI: ed. (1984) Self-Organization: Autowaves and Structures Far From Equilibrium, Springer-Verlag, New York
Langton, Chris: ed. (1988) Artificial Life, Addison-Wesley
Proceedings from first artificial life conference. Pattee, Goel, Hufford, Klir.
Lerner, D: (1963) Parts and Wholes, Free Press, New York
* Lilienfeld, Robert: (1978) Rise of Systems Theory: An Ideological Analysis, Wiley-Intersciences, New York
A good critical view of some undesirable developments in the systems movement.
Lumsden, Charles, and Wilson, Edward: (1981) Genes, Mind, and Culture: the Coevolutionary Process, Harvard, Cambridge
Non-systemic attempt at unified biological evolutionary theory. Mind as necessary explanatory component from genes to culture. Sociobiology, biological constraint and cause of behavior. Epigenetic rules, epigenesis as coevolution. Mathematical, culturgens. Euculture as human culture, vs. protoculture. Bibliography, no thermodynamics.
Mandelbrot, BB: (1982) Fractal Geometry of Nature, WH Freeman, San Francisco
Classical work on the implications of fractal geometry for modeling physical systems.
Margalef, D Ramon: (1968) Perspectives in Sociological Theory, U. Chicago, Chicago
Maturana, HR, and Varela, F: (1987) Tree of Knowledge, Shambala
On cybernetics and constructivist psychology.
McCulloch, Warren: (1965) Embodiments of Mind, MIT Press, Cambridge
Meadows, Donella H, and Meadows, Dennis L: (1972) Limits to Growth, Signet, New York, and its follow-up Beyond the Limits
Famous report of the Club of Rome. First systems dynamics model of world ecology.
Mesarovic, MD: (1964) Views of General Systems Theory, Wiley, New York
Mesarovic, MD, and Macko, D: (1970) Theory of Hierarchical Multi-Level Systems, Academic Press, New York
Mesarovic, MD, and Takahara, Y: (1975) General Systems Theory: Mathematical Foundations, Academic Press, New York
Mesarovic, MD, and Takahara, : (1988) Abstract Systems Theory, Springer-Verlag, Berlin
Grand formalism for Systems Science. Fundamental behaviorism. Teleogical (functional) and material, causal (structural) descriptions as equivalent in system-description language. Defense of formalism as a kind of language. Systems as proper relations. Cybernetic systems as goal-seeking. Complexity as meta-systems (nesting). Introductions to category theory, topology, etc. Fuzzy systems as ** open** systems.
* Miller, James G: (1978) Living Systems, McGraw Hill, New York
General synthetic theory of biological systems. On functional self-similarity across levels of analysis.
Miser, HJ, and Quade, ES: eds. (1985) Handbook of Systems Analysis, North-Holland, New York
Monod, Jacques: (1971) Chance and Necessity, Vantage, New York
Famous essay on philosophical problems concerning theories of biological systems.
Morowitz, Harold J: (1968) Energy Flow in Biology, Academic Press, New York
On the thermodynamics and informational (entropic) dynamics of biological processes.
Morrison, P: (1982) Powers of Ten, in: Scientific American Books, WH Freeman, New York
"Guided tour" through the spatial scales of natural structure.
Negoita, CV, and Ralescu, DA: (1975) Applications of Fuzzy Sets to Systems Analysis, Birkhauser, Stuttgart
* Negotia, CV: (1981) Fuzzy Systems, Abacus Press, Tunbridge-Wells
Simple, coherent introduction to fuzzy systems theory.
Nicolis, G, and Prigogine, Ilya: (1977) Self-Organization in Non-Equilibrium Systems, Wiley, New York
Technical work on self-organization in flow systems, thermodynamic systems, and other describably in terms of partial differential equations.
* Odum, HT: (1983) Systems Ecology, Wiley, New York
Grand theory of global ecology. Thermodynamic basis of economy.
Pattee, Howard: ed. (1973) Hierarchy Theory, George Braziller, New York
Phillips, DC: (1976) Holistic Thought in Social Sciences
On synthesis on holism and reductionism.
Pines, David: ed. (1988) Emerging Syntheses in Science, Addison-Wesley, New York
Includes key articles by Charles Bennett and interesting looks at spin-glasses and solitons.
Powers, WT: (1973) Behavior, the Control of Perception, Aldine, Chicago
Radical constructivist cybernetic psychological theory.
* Prigogine, Ilya: (1980) From Being to Becoming, WH Freeman, San Francisco
On the whole Prigogine program for explanation of evolution in thermodynamic terms.
..... (1984) Order Out of Chaos, Bantam, New York
Famous, almost-popular treatment of the relation between far-from-equilibrium thermodynamic, general evolutionary theory, and natural philosophy.
Rapoport, Anatol: (1984) General Systems Theory: Essential Concepts and Applications, Abacus, Cambridge
Rescher, Nicholas: Scientific Explanation
Uses stochastic automata in a philosophy of theory.
..... (1979) Cognitive Systematization, Rowman and Littlefie, Totowa, NJ
Treatment of coherentist epistemolgoy and formal development of the necessary limits to knowledge.
Rosen, Robert: (1970) Dynamical Systems Theory in Biology, Wiley-Interscience, New York
..... (1985) Anticipatory Systems, Pergamon, Oxford
The only book on anticipatory systems at present.
Rosenkrantz, Roger D: ed. (1989) ET Jaynes Papers on Prob., Statistics and Statistical Physics, Kluwer
Collection of Jayne's best papers.
Sage, AP: (1977) Methodology for Large Scale Systems, McGraw-Hill, New York
Sandquist, GM: (1985) Introduction to Systems Science, Prentice Hall, Eng. Cliffs NJ
* Sayre, Kenneth: (1976) Cybernetics and the Philosophy of Mind, Humanities Press, Atl. High., NJ
Grand cybernetic evolutionary theory of mind.
Schrodinger, : (1967) What is Life?, Cambridge U., Cambridge,
Classic essay series on foundations of biological theory.
Shafer, Glen: (1976) A Mathematical Theory of Evidence, Princeton U., Princeton
On the foundations of extended information theory, in particular extended probabilities and Dempster-Shafer evidential inference.
Shannon, CE: ed. (1956) Automata Studies, Princeton U. Press, Princeton
First and historically very important book on automata; includes von Neumann on probabilistic automata.
Shannon, CE, and Weaver, W: (1964) Mathematical Theory of Communication, U. Illinois, Urbana
Classic work on the foundations of classical information theory.
Simon, Herbert: (1969) Sciences of the Artificial, MIT, Boston
..... (1977) Models of Discovery, Reidel, Boston
Skilling, John: ed. (1989) Maximum-Entropy and Bayesian Methods, Kluwer
Proceedings of the 8th MaxEnt workshop. Statistical thermodynamics and quantum mechanics. Measurement, crystalography, spectroscopy, time series, power spectra, astronomy, neural nets. Fundamentals, statistics.
Skoglund, V: (1967) Similitude: Theory and Applications, Int. Textbook Co., Scranton PA
Smuts, JC: (1926) Holism and Evolution, McMillan, London
Early work on holism.
Steinbruner, JD: (1974) Cybernetic Theory of Decision, Princeton U, Princeton
Susiluoto, I: (1982) Origins and Development of Systems Thinking in USSR, in: Annales Acad. Scie.,Diss.HumanLitt., v. 30, Finnish Acad. Sci., Helsinki
* Szucz, E: (1980) Similitude and Modeling, Elsevier, New York,
Probably the most modern book on the theory of similarity.
Theil, H: (1967) Economics and Information Theory, Rand McNally, Chicago
Classic work on the use of information theory in economic theory.
Thom, Rene: (1975) Structural Stability and Morphogenesis, Addison-Wesley, Reading MA
..... (1983) Mathematical Models of Morphogenesis, Ellis Hortwood Ltd., New York
Topological approach to systems philosophy, catastrophe theory, dynamical systems.
Thompson, D'Arcy: (1959) On Growth and Form, Cambridge U., Cambridge
Classic work in early cybernetic biological theory.
Trappl, Robert: ed. (1983) Cybernetics: Theory and Applications, Hemisphere, Washington
Anthology of foundations of systems and cybernetics; review of applications; complete bibliography. Beer, Atlan, Pichler, Klir, Pask, Nowakowska, Arbib, Laszlo.Trappl, Robert, and Horn, W, et. al.: eds. (1984) Basic and Applied General Systems Research: Bibliography, IFSR, Laxenburg,Aust., NOTE: From 1977-1984
Turchin, Valentin: (1977) Phenomenon of Science, Columbia U., New York
Cybernetic theory of universal evolution. Metascience as a cybernetic enterprise...... (1981) Inertia of Fear and Scientific Worldview, Columbia U. Press, New York
Interpretation of totalitarianism from the persepctive of cybernetic social theory.** von Bertalanffy, Ludwig: (1968) General Systems Theory, George Braziller, New York
Van Laarhove, PJ, and Aarts, EHL: (1987) Simulated Annealing: Theory and Applications, Kluwer
On phase transitions.Varela, FG: (1979) Principles of Biological Autonomy, North Holland, New York
von Foerster, Heinz: (1979) Cybernetics of Cybernetics, ed. K. Krippendorf, GordonandBreach, New York
ed. (1981) Observing Systems, Intersystems, Seaside CA
Many classic early cybernetics essays. On self-organization,memory without record (non-localized representation), computation of neural nets, necessities of biological function. Later essays on self-referential psychology much weaker.von Foerster, Heinz, and Zopf, G.: eds. (1962) Principles of Self-Organization, Pergamon, New York
von Neumann, John: (1958) Computer and the Brain, Yale U., New Haven
Classical essay on the theoretical foundations of cognitive science...... (1966) Theory of Self-Reproducing Automata, U. Illinois, Urbana Ill.
Waddington, CH: (1977) Tools for Thought, Cape, London
Warfield, JN: (1976) Societal Systems, Wiley-Interscience, New York
Wartofsky, MW: (1979) Models, Reidel, Boston
Weber, Bruce: ed. (1988) Entropy, Information, and Evolution, MIT Press, Cambridge
Primary reference. Wicken, Wiley, Brooks. Cities as dissipative structures.
* Weinberg, Gerard M.: (1975) An Introduction to General Systems Thinking, Wiley, New York
A readable and insightful book...... (1988) Rethinking Systems Analysis and Decision, Dorset House, New York
Weir, M: (1984) Goal-Directed Behavior, Gordon and Breach
Wicken, Jeffrey: (1987) Evolution, Information and Thermodynamics, Oxford U., New York
** Wiener, Norbert: (1948) Cybernetics. or Control and Communication in the Animal and Machine, MIT Press, Cambridge On the Human Use of Human Beings: Cybernetics and Society
Wilden, Anthony: (1972) System and Structure, Tavistock, New York
Series of fascinating, polemical essays on a vast variety of subjects critical to systems and cybernetics and their relations to depth psychology, politics, and world culture.Wilson, B: (1984) Systems: Concepts, Methodologies, and Applications, Wiley, Chichester UK
Windeknecht, TG: (1971) General Dynamical Processes, Academic Press, New York
Wolfram, Steven: ed. (1986) Theory and Applications of Cellular Automata, Scientific Press
Wymore, AW: (1969) Mathematical Theory of Systems Engineering, Wiley, New York
..... (1976) Systems Engineering Methodology for Interdisc. Theory, Wiley, New York
Wymore, Wayne: Systems Theory
Yates, Eugene: ed. (1987) Self-Organizing Systems: the Emergence of Order, Plenum, New York
Critical collection on self-organizing systems. Includes Iberall, Morowitz, Arbib, Pattee, Haken, Caianiello, Abraham and Shaw.Zadeh, Lofti A: (1954) System Theory, in: Columbia Eng. Quart., v. 8, pp. 16-19
Zadeh, Lofti A, and Desoer, CA: (1963) Linear Systems Theory, Mcraw-Hill, New York
Zeeman, EC: (1977) Catastrophe Theory, Addison Wesley, Reading, MA
Development of hysteresis and catastrophe theory as a modeling tool for systems science.Zeigler, BP: (1976) Theory of Modeling and Simulation, Wiley, New York
Zeigler, BP, and Elzas, MS et. al.: eds. (1979) Methodology in Systems Modeling and Simulation, North-Holland, New York
Zeleny, Milan: ed. (1981) Autopoiesis: A Theory of Living Organization, North-Holland, New York
Critical anthology on this theory of self-organization, including Maturana and Varela.
All of the classic, "required" papers have been reprinted in the book: Klir G.J. (1992) Facets of Systems Science, (Plenum, New York). You can order photocopies of many papers via the CARL UnCover service, which provides a search through a database containing millions of papers in thousands of academic journals covering all disciplines. Other, specific bibliographic references of books and a selected number of papers can be found in the library database of the Department of Medical Cybernetics and AI at the University of Vienna. A number of more recent books and papers can be found in our bibliography on complex, evolving systems, and in the bibliography of the Principia Cybernetica Project.
Key: * Required
R Recommended
Abraham, Ralph: (1987) "Dynamics and Self-Organization", in:
/Self-Organizing Systems/, ed. Eugene Yates, pp. 599-616, Plenum
Review of the scope and extent of modern dynamics theory,
especially as related to problems in self-organization. Useful
after an elementary understanding of dynamical systems.
Abraham, Ralph, and Shaw, Christophe: (1987) "Dynamics: a
Visual Introduction", in: /Self-Organizing Systems: Emergence/,
ed. Eugene Yates, pp. 543-598, Plenum
Ackoff, Russel: (1979) "Future of Operational Research is
Past", /General Systems Yearbook/, v. 24, pp. 241-252
R Arbib, Michael A: (1966) "Automata Theory and Control Theory: A
Rapproachement", /Automatica/, v. 3, pp. 161-189
A unification of automata theory and control theory in a broader
theory of dynamic systems.
Arbib, Michael A, and Rhodes, JL et. al.: (1968) "Complexity and
Graph Complexity of Finite State Machines and Finite Semi-Groups",
in: /Algorithmic Theory of Machines, Languages and Semi-Groups/,
ed. MA Arbib, pp. 127-145, Academic Press, New York
A rigorous formulation of descriptive complexity of systems in
terms of finite state machines.
* Ashby, Ross: (1958) "General Systems Theory as a New
Discipline", /General Systems Yearbook/, v. 3:1
* (1958) "Requisite Variety and Implications for Control of Complex
Systems", /Cybernetica/, v. 1, pp. 83-99
* (1964) "Introductory Remarks at Panel Discussion", in: /Views
in General Systems Theory/, ed. M. Mesarovic, pp. 165-169, Wiley,
New York
(1965) "Measuring the Internal Informational Exchange in a
System", /Cybernetica/, v. 1, pp. 5-22
A readable paper that explains how the Shannon entropy can be
used in analyzing systems.
(1968) "Some Consequences of Bremermann's Limit for Information
Processing Systems", in: /Cybernetic Problems in Bionics/, ed.
H Oestreicher et. al, pp. 69-76, Gordon and Breach, New York
(1970) "Information Flows Within Coordinated Systems", /Progress
in Cybernetics/, v. 1, ed. J. Rose, pp. 57-64, Gordon and Breach,
London
(1972) "Systems and Their Informational Measures", in: /Trends in
General Systems Theory/, ed. GJ Klir, pp. 78-97, Wiley, New York,
* (1973) "Some Peculiarities of Complex Systems", /Cybernetic
Medicine/, v. 9:2, pp. 1-6
Atlan, Henri: (1981) "Hierarchical Self-Organization in Living
Systems", in: /Autopoises/, ed. Milan Zeleny, North Holland, New
York
Auger, Peter: (1989) "Microcanonical Ensembles with
Non-equiprobable States", /Int. J. Gen. Sys./, v. 20:3, pp.
457-466
Aulin, AY: (1975) "Cybernetics as Foundational Science of
Action", /Cybernetic/, v. 3
* (1979) "Law of Requisite Hierarchy", /Kybernetes/, v. 8, pp.
259-266
Bahm, AJ: (1981) "Five Types of Systems Philosophies", /Int. J.
Gen. Sys./, v. 6
(1983) "Five Systems Concepts of Society", /Behavoral Science/,
v. 28
(1984) "Holons: Three Conceptions", /Systems Research/, v. 1:2,
pp. 145-150
Comparison of three system philosophies.
(1986) "Nature of Existing Systems", /Systems Research/, v. 3:3,
Pergamon, Oxford
Philosophical analysis of the necessary and sufficient conditions
for systemic processes.
(1988) "Comparing Civilizations as Systems", /Systems Research/,
v. 5:1
Macroscopic structural, semantic analysis of cultural systems.
Bailey, Kenneth D: (1984) "Equilibrium, Entropy and
Homeostasis", /Systems Research/, v. 1:1, pp. 25-43
Excellent survey of these concepts in multiple disciplines.
Balakrishnan, AV: "On the State Space Theory of Linear
Systems", /J. Mathematical Analysis and Appl./, v. 14:3, ed.
1966, pp. 371-391
* Barto, AG: (1978) "Discrete and Continuous Model", /Int. J.
Gen. Sys./, v. 4:3, pp. 163-177
Bennett, Charles H: (1986) "On the Nature and Origin of Complexity
in Discrete, Homogeneous, Locally-Interacting Systems",
/Foundations of Physics/, v. 16, pp. 585-592
On Bennett's measure of algorithmic depth.
Black, M: (1937) "Vagueness: An Exercise in Logical Analysis",
/Philosophy of Science/, v. 4, pp. 427-455
Probably the best discussion of the meaning of vagueness and its
importance in science and philosophy.
* Boulding, Ken: (1956) "General Systems Theory - The Skeleton of
Science", /General Systems Yearbook/, v. 1, pp. 11-17
(1968) "Specialist with a Universal Mind", /Management Science/,
v. 14:12, pp. B647-653
* (1974) "Economics and General Systems", /Int. J. Gen. Sys./, v.
1:1, pp. 67-73
Bovet, DP: (1988) "An Introduction to Theory of Computational
Complexity", in: /Measures of Complexity/, ed. L Peliti, A
Vulpiani, pp. 102-111, Springer-Verlag, New York
Braitenberg, Valentino: "Vehicles: Expirement in Synthetic
Psychology", /IEEE Trans. of Syst., Man, and Cyb./
On the complex, seemingly lifelike behavior of simply designed
cybernetic robots.
* Bremermann, HJ: (1962) "Optimization Through Evolution and
Recombination", in: /Self-Organizing Systems/, ed. MC Yovits et.
al., pp. 93-106, Spartan, Washington DC
(1967) "Quantifiable Aspects of Goal-Seeking Self-Org. Systems",
in: /Progress in Theoretical Biology/, v. M Snell, pp. 59-77,
Academic Press, New York
Brillouin, Leon: (1953) "Negentropy Principle of Information",
/J. of Applied Physics/, v. 24:9, pp. 1152-1163
First Brillouin essay, on the relation between thermodynamic and
informational entropies.
* Bunge, Mario: (1978) "General Sys. Theory Challenge to
Classical Philosophy of Science", /Int. J. Gen. Sys./, v. 4:1
(1981) "Systems all the Way", /Nature and Systems/, v. 3:1, pp.
37-47
Carnap, Rudolph, and Bar-Hillel, Y: (1952) "Semantic
Information", /British J. for Philosopy of Science/, v. 4, pp.
147-157
Cavallo, RE, and Pichler, F: (1979) "General Systems
Methodology: Design for Intuition Ampl.", in: /Improving the
Human Condition/, Springer-Verlag, New York
Caws, P: (1974) "Coherence, System, and Structure", /Idealistic
Studies/, v. 4, pp. 2-17
Chaitin, Gregory J: (1975) "Randomness and Mathematical Proof",
/Scientific American/, v. 232:5
(1977) "Algorithmic Information Theory", /IBM J. Res. Develop./,
v. 21:4, pp. 350-359
Introduction of Chaitin's version of Kolmogorov complexity.
(1982) "Godel's Theorem and Information", /Int. J. Theoretical
Physics/, v. 22
* Checkland, Peter: (1976) "Science and Systems Paradigm", /Int.
J. Gen. Sys./, v. 3:2, pp. 127-134
Chedzey, Clifford S, and Holmes, Donald S: (1976) "System
Entropies of Markov Chains", /General Systems Yearbook/, v. XXI,
pp. 73-85
(1977) "System Entropy and the Monotonic Approach to Equilibrium",
/General Systems Yearbook/, v. 22, pp. 139-142
(1977) "System Entropy of a Discrete Time Probability Function",
/General Systems Yearbook/, v. 22, pp. 143-146
(1977) "First Discussion of Markov Chain System Entropy Applied
to Physics", /General Systems Yearbook/, v. 22, pp. 147-167
Cherniak, Christophr: (1988) "Undebuggability and Cognitive
Science", /Communications of the ACM/, v. 31:4
Like Bremmerman's limit, some simple mathematics on the limits of
computational methods.
Christensen, Ronald: (1985) "Entropy Minimax Multvariate
Statistical Modeling: I", /Int. J. Gen. Sys./, v. 11
R Conant, Roger C: (1969) "Information Transfer Required in
Regulatory Processes", /IEEE Trans. on Sys. Sci. and Cyb./, v. 5:4,
pp. 334-338
A discussion of the use of the Shannon entropy in the study of
regulation.
R (1974) "Information Flows in Hierarchical Systems", /Int. J.
Gen. Sys./, v. 1, pp. 9-18
Using classical (Shannon) information theory, it is shown that
hierarchical structures are highly efficient in information
processing.
* (1976) "Laws of Information Which Govern Systems", /IEEE Trans.
Sys., Man & Cyb./, v. 6:4, pp. 240-255
* Conant, Roger C, and Ashby, Ross: (1970) "Every Good Regulator
of Sys. Must Be Model of that Sys.", /Int. J. Systems Science/,
v. 1:2, pp. 89-97
Cornacchio, Joseph V: (1977) "Systems Complexity: A
Bibliography", /Int. J. Gen. Sys./, v. 3, pp. 267-271
De Raadt, JDR: (1987) "Ashby's Law of Requisite Variety: An
Empirical Study", /Cybernetics and Systems/, v. 18:6, pp.
517-536
R Eigen, M, and Schuster, P: (1977) "Hypercycle: A Principle of
Natural Self-Org.", /Naturwissenschaften/, v. 64,65
Classical work on molecular feedback mechanisms.
Engell, S: (1984) "Variety, Information, and Feedback",
/Kybernetes/, v. 13:2, pp. 73-77
Erlandson, RF: (1980) "Participant-Oberver in Systems
Methodologies", /IEEE Trans. on Sys., Man, and Cyb./, v. SMC-10:1,
pp. 16-19
Ferdinand, AE: (1974) "Theory of Systems Complexity", /Int. J.
Gen. Sys./, v. 1:1, pp. 19-33
A paper that connects defect probability with systems complexity
through the maximum entropy principle. Also investigates the
relationship between modularity and complexity.
Ford, Joseph: (1986) "Chaos: Solving the Unsolvable, Predicting
the Unpredictable", in: /Chaotic Dynamics and Fractals/,
Academic Press
Fascinating account of the relation between chaotic dynamics, the
limits of observability, constructive mathematics, exsitence and
uniqueness, and the "ideology" of the scientific community.
Gaines, Brian R: "An Overview of Knowledge Acquisition and Transfer",
/IEEE Proc. on Man and Machine/, v. 26:4
GSPS type methods as the general form of all science. Relation
of Klir's GSPS methodology to other inductive methodologies.
R (1972) "Axioms for Adaptive Behavior", /Int. J. of Man-Machine
Studies/, v. 4, pp. 169-199
Perhaps the most comprehenseive foundational work on adaptive
systems.
* (1976) "On the Complexity of Causal Models", /IEEE Trans. on
Sys., Man, & Cyb./, v. 6, pp. 56-59
R (1977) "System Identification, Approximation and Complexity",
/Int. J. Gen. Sys./, v. 3:145, pp. 145-174
A thorough discussion on the relationship among complexity,
credibiilty, and uncertainty associated with systems models.
* (1978) "Progress in General Systems Research", in: /Applied
General Systems Research/, ed. GJ Klir, pp. 3-28, Plenum, New
York
* (1979) "General Systems Research: Quo Vadis?", /General Systems
Yearbook/, v. 24, pp. 1-9
* (1983) "Precise Past - Fuzzy Future", /Int. J. Man-Machine
Studies/, v. 19, pp. 117-134
* (1984) "Methodology in the Large: Modeling All There Is",
/Systems Research/, v. 1:2, pp. 91-103
R Gallopin, GC: "Abstract Concept of Environment", /Int. J. Gen.
Sys./, v. 7:2, pp. 139-149
A rare discussion of the concept of environment by a well known
ecologist.
Gardner, MR: (1968) "Critical Degenerotes in Large Linear
Systems", /BCL Report/, v. 5:8, EE Dept., U. Ill, Urbana
A report on an experimental investigation whose purpose is to
determine the relationship between stability and connectance of
linear systems.
* Gardner, MR, and Ashby, Ross: (1970) "Connectance of Large
Dynamic (Cybernetic) Systems", /Nature/, v. 228:5273, pp. 784
Gelfland, AE, and Walker, CC: (1977) "Distribution of Cycle
Lengths in Class of Abstract Sys.", /Int. J. Gen. Sys./, v. 4:1,
pp. 39-45
* Goguen, JA, and Varela, FJ: (1979) "Systems and Distinctions:
Duality and Complementarity", /Int. J. Gen. Sys./, v. 5:1, pp.
31-43
Gorelick, George: (1983) "Bogdanov's Tektology: Naure,
Development and Influences", /Studies in Soviet Thought/, v. 26,
pp. 37-57
Greenspan, D: (1980) "Discrete Modeling in Microcosm and
Macrocosm", /Int. J. Gen. Sys./, v. 6:1, pp. 25-45
* Hall, AS, and Fagan, RE: (1956) "Definition of System",
/General Systems Yearbook/, v. 1, pp. 18-28
Harel, David: (1988) "On Visual Formalisms", /Communications of
the ACM/, v. 31:5
Reasonable, critical extensions of "Venn Diagrams", general
consideration of the representation of multidimensional systems.
Henkind, Steven J, and Harrison, Malcolm C: (1988) "Analysis of
Four Uncertainty Calculi", /IEEE Trans. Man Sys. Cyb./, v. 18:5,
pp. 700-714
On Bayesian, Dempster-Shafer, Fuzzy Set, and MYCIN methods of
uncertainty management.
Herbenick, RM: (1970) "Peirce on Systems Theory", /Transaction
of the S. Peirce Soc./, v. 6:2, pp. 84-98
R Huber, GP: (1984) "Nature and Design of Post-Industrial
Organizations", /Management Science/, v. 30:8, pp. 928-951
Excellent paper discussing the changing nature of organizations
in the information society.
* Islam, S: (1974) "Toward Integrating Two Systems Theories By
Mesarovic and Wymore", /Int. J. Gen. Sys./, v. 1:1, pp. 35-40
Jaynes, ET: (1957) "Information Theory and Statistical
Mechanics", /Physical Review/, v. 106,108, pp. 620-630
A classic paper. Information theory as a sufficient and elegant
basis for thermodynamics. But does it follow that thermodynamics
is necessarily dependent on information theory, or that entropy
is "just" incomplete knowledge? Compares principle of maximum
entropy with assumptions of ergodicity, metric transitivity,
and/or uniform a priori distributions. Prediction as microscopic
to macroscopic explanation; interpretation as macro to micro.
Johnson, Horton A.: (1970) "Information Theory in Biology After
18 Years", /Science/, v. 6/26/70
Scathing critique of the role of "classical" information theory
in biological science. Most of these criticisms are still
unanswered, if being addressed in a roundabout way (e.g.
algorithmic complexity theory).
Joslyn, Cliff: (1988) "Review: Works of Valentin Turchin",
/Systems Research/, v. 5:1
Short introduction to Turchin's cybernetic theories of universal
evolution.
* Kampis, G: (1989) "Two Approaches for Defining 'Systems'",
/Int. J. Gen. Sys./, v. 15, pp. 75-80
Kaufmann, Stuart A: (1969) "Metabolic StabilityandEpigenesis in
Randomly Constructed Genetic Nets", /Journal of Theoretical Biology/,
v. 22, pp. 437-467
(1984) "Emergent Properties in Random Complex Automata",
/Physica/, v. 10D, pp. 145
Kellerman, E: (1968) "Framework for Logical Cont.", /IEEE
Transactions on Computers/, v. E-17:9, pp. 881-884
Klapp, OE: (1975) "Opening and Closing in Open Systems",
/Behav. Sci./, v. 20, pp. 251-257
Philosophy on the dynamics of social processes; entropic
metaphors.
R Klir, George: (1970) "On the Relation Between Cybernetics and
Gen. Sys. Theory", in: /Progress in Cybernetics/, v. 1, ed. J
Rose, pp. 155-165, Gordon and Breach, London
A formal discussion on the relation between the fields of
"cybernetics" and "systems science", concluding that the former
is a subfield of the latter.
(1972) "Study of Organizations of Self-Organizing Systems", in:
/Proc. 6th Int. Congress on Cyb./, pp. 162-186, Wammer, Belgium
(1976) "Ident. of Generative Structures in Empirical Data", /Int.
J. Gen. Sys./, v. 3:2, pp. 89-104
(1978) "General Systems Research Movement", in: /Sys. Models for
Decision Modeling/, ed. N Sharif et. al., pp. 25-70, Asian Inst.
Tech., Bangkok
* (1985) "Complexity: Some General Observations", /Systems
Research/, v. 2:2, pp. 131-140
* (1985) "Emergence of 2-D Science in the Information Society",
/Systems Resarch/, v. 2:1, pp. 33-41
* (1988) "Systems Profile: the Emergence of Systems Science",
/Systems Research/, v. 5:2, pp. 145-156
Klir, George, and Way, Eileen: (1985) "Reconstructability
Analysis: Aims, Results, Problems", /Systems Research/, v. 2:2,
pp. 141-163
Introduction to the methods of reconstruction as well as their
relevance to general philosophical problems.
Kolmogorov, AN: (1965) "Three Approaches to the Quantitative Definition
of Information", /Problems of Information Transmission/, v. 1:1,
pp. 1-7
First introduction of algorithmic meatrics of complexity and
information.
Krippendorf, Klaus: (1984) "Epistemological Foundation for
Communication", /J. of Communication/, v. 84:Su
On the necessary cybernetics of communication.
Krohn, KB, and Rhodes, JL: (1963) "Algebraic Theory of
Machines", in: /Mathematical Theory of Automata/, ed. J. Fox, pp.
341-384, Ploytechnic Press, Brooklyn NY
(1968) "Complexity of Finite Semigroups", /Annals of
Mathematics/, v. 88, pp. 128-160
Layzer, David: (1988) "Growth of Order in the Universe", in:
/Entropy, Information, and Evolution/, ed. Bruce Weber et. al.,
pp. 23-40, MIT Press, Cambridge
On the thermodynamics of cosmological evolution, and the
necessity of "self-organization" in an expanding universe.
* Lendaris, GG: (1964) "On the Definition of Self-Organizing
Systems", /IEEE Proceedings/, v. 52, pp. 324-325
R Lettvin, JY, and Maturana, HR: (1959) "What the Frog's Eye Tell
the Frog's Brain", /Proceedings of the IRE/, v. 47, pp.
1940-1951
Classic early paper in cybernetics, cited as the basis of
"constructive" psychological theory.
Levin, Steve: (1986) "Icosahedron as 3D Finite Element in
Biomechanical Supp.", in: /Proc. 30th SGSR/, v. G, pp. 14-23
R (1989) "Space Truss as Model for Cervical Spine Mechanics",
NOTE: Manuscript
Startling theory of the necessary foundations of biomechanics in
2-d triangular (heaogonal) plane packing and 3-d dodecahedral
space packing.
Lloyd, Seth, and Pagels, Heinz: (1988) "Complexity as
Thermodynamic Depth", /Annals of Physics/, v. 188, pp. 1
Perhaps a classic, on their new measure as the difference betwen
fine and coarse entropy. Comparison with other measures of
depth, complexity, and information.
* Lofgren, Lars: (1977) "Complexity of Descriptions of Sys: A
Foundational Study", /Int. J. Gen. Sys./, v. 3:4, pp. 197-214
Madden, RF, and Ashby, Ross: (1972) "On Identification of
Many-Dimensional Relations", /Int. J. of Systems Science/, v. 3,
pp. 343-356
An early paper contributing to the area that is known now as
reconstructibility analysis.
Makridakis, S, and Faucheux, C: (1973) "Stability Properties of
General Systems", /General Systems Yearbook/, v. 18, pp. 3-12
Makridakis, S, and Weinstraub, ER: (1971) "On the Synthesis of
General Systems", /General Systems Yearbook/, v. 16, pp. 43-54
Margalef, D Ramon: (1958) "Information Theory in Ecology",
/General Systems Yearbook/, v. 3, pp. 36-71
* Marschal, JH: (1975) "Concept of a System", /Philosophy of
Science/, v. 42:4, pp. 448-467
* May, RM: (1972) "Will a Large Complex System be Stable?",
/Nature/, v. 238, pp. 413-414
McCulloch, Warren, and Pitts, WH: "Logical Calculus of Ideas
Immanent in Nervous Activity", /Bull. Math. Biophysics/, v. 5
Classic early work on the neural nets as a logical modeling
tool.
McGill, WJ: (1954) "Multivariate Information Transmission",
/Psychometrica/, v. 19, pp. 97-116
Mesarovic, MD: (1968) "Auxiliary Functions and Constructive
Specification of Gen. Sys.", /Mathematical Systems Theory/,
v. 2:3
R Miller, James G: (1986) "Can Systems Theory Generate Testable
Hypotheses?", /Systems Research/, v. 3:2, pp. 73-84
On systems theoretic research programs attempting to unify
scientific theory through hypothesized isomorphies among levels
of analysis.
Negoita, CV: (1989) "Review: Fuzzy Sets, Uncertainty, and
Information", /Kybernetes/, v. 18:1, pp. 73-74
Good analysis of the significance of fuzzy set theory.
Pattee, Howard: "Evolution of Self-Simplifying Systems", in:
/Relevance of GST/, ed. Ervin Laszlo, George Braziller, New York,
"Instabilities and Information in Biological Self-Organization",
in: /Self Organizing Systems/, ed. F. Eugene Yates, Plenum, New York
(1973) "Physical Problems of Origin of NaturalControl", in:
/Biogenesis, Evolution, Homeostasis/, ed. A. Locker,
Springer-Verlag, New York
(1978) "Complementarity Principle in Biological and Social Structures",
/J. of Social and Biological Structures/, v. 1
(1985) "Universal Principle of Measurement and Language Function in
Evolving Systems", in: /Complexity, Language, and Life/, ed. John
Casti, pp. 268-281, Springer-Verlag, Berlin
(1988) "Simulations, Realizations, and Theories of Life", in:
/Artificial Life/, ed. C Langton, pp. 63-77, Addison-Wesley,
Redwood City CA
Patten, BC: (1978) "Systems Approach to the Concept of
Environment", /Ohio J. of Science/, v. 78:4, pp. 206-222
Pearl, J: (1978) "On Connection Between Complexity and Credibility of
Inferred Models", /Int. J. Gen. Sys./, v. 4:4, pp. 255-264
Theoretical study that shows that credibility of determinstic
models inferred from data tends to increase with data size and
decrease with the complexity of the model.
Pedrycz, W: (1981) "On Approach to the Analysis of Fuzzy
Systmes", /Int. J. of Control/, v. 34, pp. 403-421
Peterson, JL: (1977) "Petri Nets", /ACM Computing Surveys/, v.
9:3, pp. 223-252
R Pippenger, N: (1978) "Complexity Theory", /Scientific
American/, v. 238:6, pp. 114-124
Excellent discussion of one facet of complexity.
* Porter, B: (1976) "Requisite Variety in the Systems and Control
Sciences", /Int. J. Gen. Sys./, v. 2:4, pp. 225-229
Prigogine, Ilya, and Nicolis, Gregoire: (1972) "Thermodynamics
of Evolution", /Physics Today/, v. 25, pp. 23-28
Briefer introduction to far-from-equilibrium thermodynamics,
hypercycles, and evolutionary theory. Criticzed as confused.
Rapoport, Anatol: (1962) "Mathemantical Aspects of General
Systems Theory", /General Systems Yearbook/, v. 11, pp. 3-11
Rivier, N: (1986) "Structure of Random Cellular Networks and
Their Evolution", /Physica/, v. 23D, pp. 129-137
Brilliant introduction to the theory of the equilibrium
distribution of macroscopic entities (cells) in multiple kinds of
substances: metals, soap suds, and animal and vegetable tissues;
according to a non-thermodynamic maximum entropy law. Subsumes
other laws from these specific disciplines.
(1988) "Statistical Geometry of Tissues", in: /Thermodynamics and
Pattern Formation in Biology/, pp. 415-445, Walter de Gruyter,
New York
* Rosen, Robert: (1977) "Complexity as a Systems Property", /Int.
J. Gen. Sys./, v. 3:4, pp. 227-232
* (1978) "Biology and Systems Resarch", in: /Applied General
Systems Research/, ed. GJ Klir, pp. 489-510, Plenum, New York
* (1979) "Anticipatory Systems", /General Systems Yearbook/, v.
24, pp. 11-23
* (1979) "Old Trends and New Trends in General Systems Resarch",
/Int. J. Gen. Sys./, v. 5:3, pp. 173-184
* (1981) "Challenge of Systems Theory", /General Systems
Bulletin/
* (1985) "Physics of Complexity", /Systems Research/, v. 2:2, pp.
171-175
* (1986) "Some Comments on Systems and Systems Theory", /Int. J.
Gen. Sys./, v. 13:1, pp. 1-3
Rosenbluth, Arturo, and Wiener, Norbert: (1943) "Behavior,
Purpose, and Teleology", /Philosophy of Science/, v. 10, pp.
18-24
Original introduction of teleonomy, teleology, goal-seeking, and
intentionality in cybernetic terms.
Rothstein, J: (1979) "Generalized Entropy, Boundary Conditions,
and Biology", in: /Maximum Entropy Formalism/, ed. RD Levine, pp.
423-468, Cambridge U., Cambridge
On boundary conditions in biology, organisms as "well-informed
heat engines", definition of mutual information, order as an
entropy measure.
Sadovsky, V: (1979) "Methodology of Science and Systems
Approach", /Social Science/, v. 10, Moscow
Saperstein, Alvin M.: (1984) "Chaos: A Model for the Outrbreak
of War", /Nature/, v. 309
Schedrovitzk, GP: (1962) "Methdological Problems of Systems
Research", /General Systems Yearbook/, v. 11, pp. 27-53
Schneider, Eric D: (1988) "Thermodynamics, Ecological Succession and
Natural Selection: A Common Thread", in: /Entropy, Information, and
Evolution/, pp. 107-138, Bruce Weber et. al., Cambridge
On the thermodynamics of maturing ecosystems, relation to
Principle of Maximum Entropy Production.
Shaw, Robert: (1981) "Strange Attractors, Chaotic Behavior and
Information Flow", /Zeitschrift fur Naturforschung/, v. 36a
(1984) /Dripping Faucet as a Model Chaotic System/, Aeriel Press,
Santa Cruz
Best explanation of the nature of chaotic processes, especially
with respect to information theory.
Simon, Herbert: (1965) "Architecture of Complexity", /General
Systems Yearbook/, v. 10, pp. 63-76
* (1988) "Predication and Prescription in Systems Modeling",
NOTE: IIASA manuscript
Skarda, CA, and Freeman, WJ: (1987) "How Brains Make Chaos Into
Order", /Behavioral and Brain Sciences/, v. 10
Interpretation of neurological experiments revealing the
cybernetic basis of perception, the reliance on chaotic dynamics,
and the non-locality of mental representations. Resting as
chaos, perception as stable attractors, seizures as cyclic
attractos.
Skilling, John: (1989) "Classic Maximum Entropy", in: /Maximum
Entropy and Bayesian Methods/, ed. J. Skilling, pp. 45-52, Kluwer,
New York
Mathematical introduction to the traditonal MaxEnt method as
applied to data analysis.
Smith, C Ray: (1990) "From Rationality and Consistency to
Bayesian Probability", in: /Maximum Entropy and Bayesian Methods/,
ed. P. Fougere, Kluwer, New York
Mathematical introduction to the relation between inductive and
deductive reasoning, Cox's axioms, Bayes' theorem, and Jaynes'
MaxEnt program.
Smith, RL: (1989) "Systemic, not just Systematic", /Systems
Research/, v. 6:1, pp. 27-37
* Svoboda, A: "Model of the Instinct of Self-Preservation", in:
/MISP: A Simulation of a Model.../, ed. KA Wilson, NOTE: From
French,Inf.Proc.Mach. 7
Swenson, Rod: (1989) "Emergent Attractors and Law of Maximum Entropy
Production", /Systems Research/, v. 6:3, pp. 187-198
Good references for general evolution. Discussion of minimax
entropy production and emergence, biological thermodynamics.
Szilard, L: (1964) "On Decrease of Enteopy in Thermodynamic Systems by
Intervention of Intelligent Beings", /Behavioral Science/, v. 9
Classic first paper on the necessary relation between
informational and thermodynamic entropies.
Takahara, Y, and Nakao, B: (1981) "Characterization of
Interactions", /Int. J. Gen. Sys./, v. 7:2, pp. 109-122
Takahara, Y, and Takai, T: (1985) "Category Theoretical
Framework of General Systems", /Int. J. Gen. Sys./, v. 11:1, pp.
1-33
Thom, Rene: (1970) "Topological Models in Biology", in:
/Towards a Theoretical Biology/, v. 3, ed. CH Waddington, Aldine,
Chicago
On self-simplifying systems.
Tribus, Myron: (1961) "Information Theory as the Basis for
Thermostatistics and Thermodynamics", /J. Applied Mechanics/, v. 28,
pp. 108
Full description of the derivation of basic thermodynamics from
Jayne's maximum entropy formalism.
R Turchin, Valentin: (1982) "Institutionalization of Values",
/Worldview/, v. 11/82
Review of Turchin's social theory and defense of reviews of
_Phenomenon of Science_ and _Inertia of Fear_.
(1987) "Constructive Interpretation of Full Set Theory", /J. of
Symbolic Logic/, v. 52:1
Almost complete reconstruction of ZF set theory from a
constructivist philosophy, including implementation in the REFAL
language.
Turney, P: (1989) "Architecture of Complexity: A New
Blueprint", /Synthese/, v. 79:3, pp. 515-542
Ulanowicz, R, and Hennon, B: (1987) "Life and Production of
Entropy", /Proc. R. Soc. London/, v. B 232, pp. 181-192
Excellent: principle of maximum entropy production; positive
feedback=autocatalysis; lasers as high dissipative, low entropy
producing systems; nuclear autocatalysis as greatest source of
entropy production; measurement techniques for biotic entropy
production; all chemical organization as either extinct or in
organisms; high efficiency as high entropy production; on metrics
of evolution.
v Bertalanfy, Ludwig: (1950) "An Outline of General Systems
Theory", /British J. of Philosophy of Science/, v. 1, pp.
134-164
(1962) "General Systems Theory - A Criticial Review", /General
Systems Yearbook/, v. 7, pp. 1-20
* Varela, FG, and Maturana, HR et. al.: (1974) "Autopoiesis: the
Organization of Living Systems, its Characterization, and a Model",
/Biosystems/, v. 5, pp. 187-196
First definition of autopoeisis.
von Foerster, Heinz: (1960) "On Self-Organizing Systems and
their Environments", in: /Self-Organizing Systems/, ed. Yovitz and
Cameron, Pergamon
Well written, many interesting observations. Proof of
meaningless of the term "SOS", first (?) discussion of "growth of
phase space" route to organization, on relative information,
order from noise principle.
von Neumann, John: (1963) "General and Logical Theory of
Automata", in: /Collected Works/, v. 5, ed. AH Taub, pp. 288-328,
Pergamon
Classic. On thermodynamics and fundamental cybernetics,
digital/analog distinctions and relations in complex systems.
(1963) "Probability, Logic, and Synthesis of Reliable Organization
from Unreliable Parts", in: /Collected Works/, v. 5, ed. AH Taub,
pp. 329-378, Pergamon
On logics, automata, and information theory.
* Waelchli, F: (1989) "Eleven Theses of General Systems Theory",
/Systems Research/, NOTE: To appear
R Walker, CC: (1971) "Behavior of a Class of Complex Systems",
/J. Cybernetics/, v. 1:4, pp. 55-67
A good example of the use of the computer in discovering systems
science laws.
Walker, CC, and Ashby, Ross: (1966) "On Temporal Characteristics of
Behavior in Certain Complex Systems", /Kybernetik/, v. 3:2, pp.
100-108
Warfield, JN, and Christakis, AN: (1986) "Dimensionality",
/Systems Research/, v. 3:3, Pergamon, Oxford
R Weaire, D, and Rivier, N: (1984) "Soaps, Cells and Statistics:
Random Patterns in 2-D", /Contemporary Physics/, v. 25:1, pp.
59-99
Continution of Rivier 1986.
* Weaver, Warren: (1968) "Science and Complexity", /American
Scientist/, v. 36, pp. 536-544
From Klir, on organized simplicity, unorganized complexity, and
organized complexity.
White, I: (1988) "Limits and Capabilities of Machines: A
Review", /IEEE Trans. on Sys., Man, and Cyb./, v. 18:6, pp.
917-938
Wicken, Jeffrey: (1987) "Entropy and Information: Suggestions
for a Common Language", /Philosphy of Science/, v. 54:2, pp.
176-193
Solid paper on more modern view of the relation between
thermodynamics and information theory.
Wilson, David S: (1989) "Reviving the Superorganism", /J.
Theor. Bio./, v. 136, pp. 337-356
On levels of selection, criteria for being an organism, systems
vs. aggregates. Wilson is a current SUNY faculty.
Wolfram, Stephen: (1988) "Complex Systems Theory", in:
/Emerging Syntheses in Science/, ed. David Pines, pp. 183-190,
Addison-Wesley, New York
Example of a more simplistic appeal to entropy as a metric of
order.
Zadeh, Lofti A: (1958) "On the Identification Problem", /IRE
Trans. on Circuit Theory/, v. CT-3, pp. 277-281
* (1962) "From Circuit Theory to Systems Theory", /IRE
Proceedings/, v. 50, pp. 856-865
* (1963) "On the Definition of Adaptibility", /IEEE Proceedings/,
v. 51, pp. 469-470
(1963) "General Identification Problem", in: /Proceedings of the
Princeton Conference on the Identification Problem in Communications
and Control/, pp. 1-17
(1965) "Fuzzy Sets and Systems", in: /Systems Theory/, ed. J.
Fox, pp. 29-37, Polytechnic Press, Brooklyn NY
R (1973) "Outline of a New Approach to Analysis of Complex Sys.",
/IEEE Trans. on Sys., Man and Cyb./, v. 1:1, pp. 28-44
A motivation for using fuzziness in dealing with very complex
systems is discussed in detail.
(1982) "Fuzzy Systems Theory: Framework for Analysis of Buerocratic
Systems", in: /Sys. Meth. in Social Science Res./, ed. RE Cavallo,
pp. 25-41, Kluwer-Nijhoff, Boston
R Zeigler, BP: (1974) "Conceptual Basis for Modeling and
Simulation", /Int. J. Gen. Sys./, v. 1:4, pp. 213-228
A solid systems science conceptual framework for modeling and
simulation is introduced.
R (1976) "Hierarchy of Systems Specifications and Problems of
Structural Inference", in: /PSA 1976/, v. 1, ed. F.Suppe,
PD Asquith, pp. 227-239, Phil. Sci. Assoc., E. Lansing
Introduces a hierarchy of systems types (a formal treatment).
Zeleny, Milan: (1979) "Special Book Review", /Int. J. Gen.
Sys./, v. 5, pp. 63-71
(1988) "Tectology", /Int. J. Gen. Sys./, v. 14, pp. 331-343
On Bogdonav, an important historical figure in systems science.
Zwick, Martin: (1978) "Fuzziness and Catastrophe", in: /Proc.
of the Int. Conf. of Cyb.andSoc/, pp. 1237-1241, Tokyo/Kyoto
(1978) "Dialectics and Catastrophe", in: /Sociocybernetics/, ed.
F.Geyer et. al., pp. 129-155, Martinus Nijhoff, The Hauge,Neth.
R (1978) "Requisite Variety and the Second Law", in: /Proc. Int.
Conf. of Cyb. and Soc./, pp. 1065-1068, IEEE Sys. Man Cyb.,
Tokyo/Kyoto
Establishes the equivalence of Ashby's Requisite Variety Law and
the second law of thermodynamics.
(1978) "Quantum Measurement and Godel's Proof", /Speculations in
Science and Tech./, v. 1, pp. 135-145
R (1979) "Cusp Catastrophe and Laws of Dialectics", /System and
Nature/, v. 1, pp. 177-187
Expression of dialectical concepts (quantity to quality,
negation, interpenetration of opposites) in terms of catastrophe
theory.
(1982) "Dialectic Thermodynamics", /General Systems Yearbook/, v.
27, pp. 197-204
R (1984) "Information, Constraint, and Meaning", in: /Proceedings
SGSR/, ed. AW Smith, pp. 93-99, Intersystems
Wonderful treatment of the relation between syntax and semantics
in information theory.
Each of these books and papers is selected to be both very important to the domain, and of high quality. They are therefore highly recommended for everybody working in the domain. The number of stars (*) denotes the relative importance in terms of the number of citations. For a discussion of the main contributions of the following authors and publications, see my paper "Classic Publications on Complex, Evolving Systems: a citation-based survey" .
The books with links below can be securely ordered and paid for over the web via Amazon.com, the largest bookstore on the Net. Note: although out-of-print books too can be ordered in this way, it may be quicker to try and locate them in a public library.
Anderson P. W., K. J. Arrow, and D. Pines (Eds.). The Economy as an Evolving Complex System, Addison-Wesley, Redwood City CA, 1988. **
Arthur, W. B.: Competing Technologies, Increasing Returns, and Lock-in by Historical Events, The Economic Journal 99: 1989, pp. 106-131. *
Arthur, W. B.: Positive Feedbacks in the Economy, Scientific American, February 1990, pp. 92-99. *
Arthur W. B. Increasing Returns and Path Dependence in the Economy, University of Michigan Press, Ann Arbor, 1994.
Arthur W. B.: Bounded Rationality and Inductive Behavior (the El Farol Problem), American Economic Review 84, pp. 406-411, 1994.
Ashby W. R. An Introduction to Cybernetics, Methuen, London, 1964. **
Ashby W. R. Mechanisms of Intelligence: Writings of Ross Ashby, Intersystems, Salinas CA, 1981.
Ashby, W. R. Design for a Brain - The Origin of Adaptive Behaviour. Chapman and Hall, London, 1960.
Aulin A. The Cybernetic Laws of Social Progress, Pergamon, Oxford, 1982 *
Axelrod R. M. The Evolution of Cooperation, Basic Books, New York, 1984. *
Bak P. and Chen K.: Self-Organized Criticality, Scientific American: January 1991, pp. 46-53.
Bak P., Tang C., & Weisenfeld K.: Self-Organized Criticality. Physical Review A 38: 1988, pp. 364-374. *
Bak P., How Nature Works: The Science of Self-Organized Criticality, Springer, Berlin, 1996.
Bennett C. H. Dissipation, Information, Computational Complexity and the Definition of Organization. Emerging Syntheses in Science, Pines D. (ed.), Addison-Wesley, Redwood City CA, 1985, pp. 215-233. *
Boulding K. E. Ecodynamics: a new theory of societal evolution. Sage, London, 1978.
Campbell, D. T. Evolutionary epistemology. Evolutionary epistemology, rationality, and the sociology of knowledge, G. Radnitzky and W. W. Bartley (eds.), Open Court, La Salle IL, 1987, pp. 47-89.
Campbell, D. T. "Downward Causation" in Hierarchically Organized Biological Systems. Studies in the Philosophy of Biology, F.J. Ayala and T. Dobzhansky (eds), Macmillan, New York, 1974 .
Casti J.L. Complexification: explaining a paradoxical world through the science of surprise, HarperCollins, 1994.
Crutchfield, J., Farmer, J.D., Packard, N., and Shaw, R.: Chaos, Scientific American, 255 (6): December 1986, pp. 46-57.
Darwin C. The origin of species by means of natural selection or the preservation of favoured races in the struggle for life. (Edited with and introduction by J W Burrow). Penguin classics, 1985. (First published by John Murray, 1859) *
Dawkins R. The selfish gene (2nd edition), Oxford University Press, Oxford, 1989. **
Dawkins R. The Extended Phenotype: The Gene as a Unit of Selection, Oxford University Press, Oxford, 1983. *
Dawkins R. The Blind Watchmaker, Longman, London, 1986. *
Eigen M. and P. Schuster. The Hypercycle: A principle of natural self-organization, Springer, Berlin, 1979 **
Eigen M., and R. Winkler-Oswatitsch. Steps Toward Life: a perspective on evolution. Oxford University Press, New York, 1992. *
Fisher R. A. The Genetical Theory of Natural Selection, 2nd edition, Dover Publications, New York, 1958.
Forrester, J. Industrial Dynamics, MIT Press, Cambridge, MA, 1961.
Forrester, J. W. World Dynamics (2nd ed.), Wright-Allen Press, Cambridge, MA, 1973.
Gell-Mann, M., The Quark and the Jaguar: Adventures in the Simple and the Complex, W.H. Freeman, San Francisco, 1994. *
Gleick, J. 1987. Chaos: Making of a New Science, Penguin Books, New York. *
Gould S.J., and N. Eldredge. 1977: Punctuated equilibria: the tempo and mode of evolution reconsidered. Paleobiology 3, pp. 115-151.
Haken H. Synergetics, Springer, Berlin, 1978.
Holland J. H. 1992. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence, MIT Press, Cambridge MA. ***
Holland J.H. Hidden Order : How Adaptation Builds Complexity , Addison-Wesley 1996.
Holland J. H., Holyoak K. J., Nisbett R. E. & Thagard P. R. 1986 Induction: Processes of Inference, Learning and Discovery, MIT Press, Cambridge MA. *
Jantsch, E., The Self-Organizing Universe: Scientific and Human Implications of the Emerging Paradigm of Evolution, Oxford, Pergamon Press, 1979.*
Kauffman S. A.: Antichaos and Adaptation, Scientific American: August 1991, pp. 78-84 **
Kauffman S. A. The Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, New York, 1993 ****
Kauffman S. A. At Home in the Universe: The Search for Laws of Self-Organization and Complexity, Oxford University Press, Oxford, 1995.
Langton C. G.: Computation at the Edge of Chaos: phase transitions and emergent computation, Physica D, 42, 1-3, pp. 12-37, 1990. *
Langton, C. G. (Ed.). Artificial Life: The Proceedings of an Interdisciplinary Workshop on the Synthesis and Simulation of Living Systems, Addison-Wesley, Redwood City CA, 1989. **
Langton, C. G., Taylor, C., Farmer, J.D., and Rasmussen, S. (Eds.). Artificial Life II: Proceedings of the Second Artificial Life Workshop, Addison-Wesley, Redwood City CA, 1992. *
Langton, C. G. (ed.), Artificial Life: An Overview, MIT Press, Cambridge, MA, 1995.
Mandelbrot B. B. The Fractal Geometry of Nature, Freeman, New York, 1983.
Maruyama M.: The Second Cybernetics: Deviation-Amplifying Mutual Causal Processes, American Scientist 51, No. 2: 1963, pp. 164-179.
Maturana H. R., & Varela F. J. The Tree of Knowledge: The Biological Roots of Understanding, (rev. ed.), Shambhala, Boston, 1992. ***
Monod, J. Chance and Necessity, Collins, London, 1972.
Nicolis, G, and Prigogine, I. Self-Organization in Non-Equilibrium Systems, Wiley, New York, 1977. **
Nicolis, G. and I. Prigogine. Exploring Complexity, Freeman, New York, 1989.
Prigogine, I. and Stengers, I. Order Out of Chaos, Bantam Books, New York, 1984 ***
Prigogine, I. From Being to Becoming: Time and complexity in the physical sciences, Freeman, San Francisco, 1980.
Ray, T. S. An Approach to the Synthesis of Life. Artificial Life II, C. G. Langton et al. (Eds.), Addison-Wesley, Redwood City CA, 1992, pp. 371-408.
Shannon, C. E., and W. Weaver. The Mathematical Theory of Communication (5th ed.). University of Illinois Press, Chicago, 1963.
Simon, H. A. The Sciences of the Artificial (3rd. edition) MIT Press, Cambridge MA, 1996. **
Thom, R. Structural Stability and Morphogenesis, Benjamin, Reading MA, 1975.
Thompson, D. On Growth and Form, Cambridge University Press, Cambridge, 1917.
Varela, F., Principles of Biological Autonomy, North Holland, New York, 1979.*
von Bertalanffy L. General Systems Theory (Revised Edition), George Braziller, New York, 1973. *
von Foerster H. On self-organising systems and their environments. Self-Organising Systems, M.C. Yovits and S. Cameron (Eds.), Pergamon Press, London, 1960, pp. 30-50. *
von Foerster H. and Zopf, G. (Eds.) Principles of Self-Organization, Pergamon, New York, 1962. *
von Foerster H. Observing Systems: Selected papers of Heinz von Foerster. Intersystems, Seaside, CA, 1981.
von Foerster H. Cybernetics of Cybernetics (2nd edition). Future Systems, Minneapolis, 1996. **
von Neumann J. Theory of Self-Reproducing Automata. (Ed. by A. W. Burks), Univ. of Illinois Press, Champaign, 1966. *
Waldrop M. M. Complexity: The Emerging Science at the Edge of Order and Chaos, Simon & Schuster, New York, 1992. **
Wiener N. Cybernetics: or Control and Communication in the Animal and Machine M.I.T. Press, New York, 1961. **
Wolfram S. Cellular Automata and Complexity: Collected Papers, Addison-Wesley, Reading MA, 1994.
Zeleny M. (Ed.) 1981, Autopoiesis: A Theory of Living Organization, North Holland, New York.
In Cybernetics and Systems Science proper, many people have approached the general task of compiling large amounts of useful information. There have been efforts on the part of scholarly organizations, like the International Society for the Systems Sciences (ISSS, formerly the Society for General Systems Research (SGSR)), to develop lists of terms and concepts held in common with Cybernetics and Systems Science. There are bibliographies of systems literature [TRRHOW84], at least four dictionaries of cybernetic terms [AM84,FRC91,KRK84,MUA68], and one encyclopedia of Systems Science [SIM87]. An important contribution is the large pamphlet Education in the Systems Sciences [SNB90], detailing a great deal of information about the whole nature of Cybernetics and Systems Science and how it is carried out around the world. [CLB84] includes a substantive glossary of systems terms. We should note the GENSYS project, directed by Len Troncale, which has an ambition similar to Principia Cybernetica.
{A classic; still the finest introductory book on cybernetics and systems theory. Includes problem sets, examples, and diagrams.}
{Translation of historical foundation of systems science.}
{Philosophy of and notational system for propositional logic. Basis for a whole school of graphical approaches to classical logic.}
{Primer on Systems Science.}
{Guide to the theory and practice of management cybernetics, based on Beer. Includes extensive glossary.}
{Early systemic evolutionary theology.}
{Computer database encyclopedia of iconic symbols.}
{Excellent book on cybernetics, translated from Russian.}
{An early book that describes the nucleus of what is known now as the General Systems Problem Solver: a general framework, or language, for systems science.}
{Textbook and essay collection for a first Systems Science course.}
{Translated from German by G. Gilbertson.}
{Survey of cybernetics.}
{Eight volumes, from the perspective of technical systems and control theory; also many excellent articles of a more general methodological and philosophical nature.}
{1st edition, Winter 1990, PO Box 5805, Berkeley CA 94705 USA. "Annotated Guide to Education and Research Opportunities in the Sciences of Complexity": degree-granting programs of study; societies, associations and organizations; directory of researchers; publications: periodicals and books; bibliography; keyword and cluster index; name index.}
{Anthology of foundations of systems and cybernetics; review of applications; complete bibliography. Beer, Atlan, Pichler, Klir, Pask, Nowakowska, Arbib, Laszlo.}
{Bibliography from 1977-1984, Continuation of earlier bibliography compiled by Klir.}
{Excellent popular introduction to systems theories and principles.}
{First book on cybernetics from this master of the field.}
annotate this page if you would like to make an addition or correction. See also the list of cybernetics journals from the ASC, and ASSA's list of Systems Journals.Adaptive BehaviorComments: devoted to experimental and theoretical research on adaptive behavior in animals and in autonomous artificial systems, with emphasis on mechanisms, organizational principles, and architectures that can be expressed in computational, physical, or mathematical models.; emphasizes an approach complementary to traditional AI, in which basic abilities that allow animals to survive, or robots to perform their mission in unpredictable environments, will be studied in preference to more elaborated and human-specific abilities; explicitly takes into account the environmental feedback.
Artificial LifeBehavioral and Brain SciencesComments: Interdisciplinary journal on theoretical and experimental psychology, with emphasis on cognitive and evolutionary models. Dialog format, not afraid to deal with philosophical and theoretical issues. To be considered as a commentator , to suggest other appropriate commentators, or for information about how to become a BBS Associate, please send email to:, harnad@clarity.princeton.edu
ISSS Comments: Old journal of the Society for General Systems Research (presently ISSS). Mostly social and psychological systems theory, often withe reference to Miller's living systems theory. Emphasis on interdisciplinarity, and generalizability of results across levels. Used to be included in many citation and reference indexes as an important journal, but has gone downhill and seems to have difficulty surviving. Co-sponsored by the Inst. of Management Sciences
BioSystemsrather small journal, locally published, with systems inspired work on cognitive science and neural networks
ComplexitySanta Fe Institute. Edited by John Casti and Harold Morowitz. Contains mostly introductory and survey articles.Complexity InternationalComments: Physics journal on dynamic systems theory, complex systems theory, cellular automata and networks, etc.
Comments: rather small, locally published, but long standing journal on cybernetics
Cybernetics & Human KnowingComments: emphasis on second-order cybernetics and semiotics (board: von Glasersfeldt, Von Foerster, Luhmann, Maturana, Braten, etc.)
Cybernetics and Systems Analysis*Cybernetics and SystemsDep. of Medical Cybernetics and Artificial Intelligence, University of Vienna, Freyung 6, A-1010 Wien, Austria.Comments: Excellent technical journal on all aspects of systems theory and cybernetics.
Evolution and Cognition
Konrad Lorenz Institute for Evolution and Cognition Research, Adolf-Lorenz-Gasse 2, A-3422 Altenberg Donau, AustriaComments: interdisciplinary research on evolutionary epistemology and evolutionary systems
Evolution of CommunicationComments: origins of human language, but also the evolutionary continuum of communication in general
ISSSComments: For years the annual publication of the Int. Soc. for Gen. Sys. Res. (ISGSR, now ISSS), featuring selected publications by foundational authors. Address probably out-of-date.
Comments: Official Journal of TAKIS
Comments: new developments in all areas of control systems technology, including, but not limited to, new sensor and actuator technologies, software and hardware for real-time computing and signal processing in, control systems, tools for computer-aided design of control systems, new approaches to control system design and implementation, experimental results, distributed architectures, intelligent control, and novel applications of control engineering methods.
IEEE Transactions on Systems, Man and CyberneticsComments: Long-standing cybernetics journal from a "reputable" publisher. More towards technical systems science, still broad-minded
IFSR Newsletter*International Journal of General SystemsGordon and BreachComments: Another premiere systems science journa. Frequently technical, otherwise broad. Complexity theory, mathematical systems theory, philosophy, history.
Comments: major focus of work developing and using Soft Systems Methodology
Journal of ComplexityComments: emphasis on mathematical and computational complexity.
Journal of Complex SystemsComments: new interdisciplinary journal in the complex adaptive systems tradition, with PCP editor Cliff Joslyn in its editorial board.
Journal of Memetics - Evolutionary Models of Information TransmissionComments:the first peer-reviewed journal on memes, freely available on the Web, sponsored by the Principia Cybernetica Project.
Journal of Social and Evolutionary Systems*KybernetesComments: Excellent British journal of systems science. Sometimes technical, otherwise broad.
Open Systems & Information DynamicsComments:interdisciplinary research in mathematics, physics, engineering and life sciences; system and information-theoretic approaches dealing with control, filtering, communication, pattern recognition, chaotic dynamics, memory and cooperative behaviour in open complex systems
Comments: journal of the French systems community; articles in French and English.
Comments: In English and Spanish, Latin American Journal of systems theory .
Social SystemsComments: In German, English and French; systems theoretical work in sociology, applications of general systems concepts (inc. cognition and difference) to society, interaction and organization .
Comments: Applications of dynamical theory to social systems modeling.
Systemic Practice and Action Research PlenumComments: application of "critical systems thinking" to improving work and organization
*Systems Research international federation for systems researchComments: another central journal for the systems theory community; emphasis on social science, management and systems thinking, less on mathematics and technology
Systems Research and Information ScienceGordon and BreachThe Information SocietyTIS Web)Comments: address probably out of date
World Futures: the Journal of General EvolutionGordon and BreachComments: Edited by Ervin Laszlo, board includes Ralph Abraham, Bob Artigiani, Bela Banathy, Peter Allen, George Kampis, Vilmos Csanyi, Varela. Contents: general patterns of change and development in nature as well as society; articles, short communications, and book reviews relating to evolutionary processes in all fields of science, with special attention to multidisciplinary approaches.
American Society for Cybernetics,
Address: Am Huelsenbusch 54,
D-44803 Bochum,
New England Complex Systems Institute
The Cybernetics Society (UK)Aims of the Association:
The Association has developed and is still developing the following activities:
President: Prof. Jean Ramaekers (Belgium),
Secretariat: International Association for Cybernetics
Palais des Expositions,
Place Andre Rijkmans,
5000 Namur (Belgium)
annotate this page, or send us an email if you want to add a forum, or if you find some information to be out of date. For mailing lists, the first address mentioned is the address to which you should send mail if you want it distributed to all subscribers (for "closed" lists, such as PRNCYB-L this is only possible if you are a subscriber yourself). The subscription address is the one where you should send mail to subscribe, unsubscribe or perform other administrative commands. The maintainer address is the one of the person who is responsible for administering the list, and where you might send questions if the automatic subscription procedures somehow don't work.
There are basically three types of mailing lists:
subscribe LISTNAMEin the body of the message to the subscription address. LISTNAME is the first part (before the "@") of the list address, e.g. PRNCYB-L.
SUBSCRIBE LISTNAME Your_First_Name Your_Last_Namein the body to the subscription (LISTSERV) address. Some hosts run a similar piece of software called listproc obeying similar commands.
Directory of Scholarly E-Conferences
Listservs at the CSOLWWW-server, FTP- archiveThe basic concept accepted by members of the Control Systems Group is that all organized behavior continuously controls the portion of perceptual experience which can be influenced by the actions of organisms. This is not an article of faith. It follows from a detailed quantitative analysis of behavior, showing that action affects the very perceptions on which action is based. The action might be as simple the tightening of a muscle, and the perception as elementary as the signal generated by a sensory nerve attached to a tendon Or the action might be as complex as formulating sentences, inflections, and expressions used in a conversation, and the perception as rich as judging the effects of one's communication on the attitudes of the listener, even as the words are being spoken.
As important function of the Control Systems Group is to provide a support system for people who have become dissatisfied with the quality of explanations in their own fields, and who have come to see control theory as a source of inspiration and a tool for productive and creative work.
Discussion might include, but is not limited to:
Whole SystemsThis is an unmoderated public list. No flaming will be allowed, but frank discussions are welcome. It is pre-supposed that the participants support the general idea of creating a better future and are able to tolerate diverse viewpoints.
Wholesys-l is a very busy list with many members and a lot of traffic. If you prefer to get only a few selected postings and no discussions, you should rather subscribe to the wholeinfo-l list. On the average one or two messages a day, which are each complete in themselves, will be forwarded from wholesys-l to wholeinfo-l. You can not post to the list directly.
Systems, Values & Organizations
ThinknetInternational Society for the Systems SciencesThe Observer WebAn electronic mailing list dedicated to Systems Science and Cybernetics on the SUNY-Binghamton computer system. The list is commited to discussing a general understanding of the evolution of complex, multi-level systems like organisms, minds, and societies as informational entities containing possibly circular processes. Specific subjects include Complex Systems Theory, Self-Organizing Systems Theory, Dynamic Systems Theory, Artificial Intelligence, Network Theory, Semiotics, fractal geometry, Fuzzy Set Theory, Recursive Theory, computer simulation, Information Theory, and more.
The purposes of the list include: 1) facilitating discussion among those working in or just interested in the general fields of Systems and Cybernetics; 2) providing a means of communicating to the general research community about the work that Systems Scientists and Cyberneticians do; 3) housing a repository of electronic files for general distribution concerning Systems and Cybernetics; and 4) providing a central, public directory of working Systems Scientists and Cyberneticians.
The list is coordinated by members of the Systems Science department of the Watson School at SUNY-Binghamton, and is affiliated with the International Society for the Systems Sciences (ISSS) and the American Society for Cybernetics (ASC). Different levels and kinds of knowledge and experience are represented.
It is a common observation that our present culture lacks integration: there is an enormous diversity of "systems of thought" (disciplines, theories, ideologies, religions, ...), but they are mostly incoherent, if not inconsistent, and when confronted with a situation where more than one system might apply, there is no guidance for choosing the most adequate one. Philosophy can be defined as the search for an integrating conceptual framework, that would tie together the scattered fragments of knowledge which determine our interaction with the world. Since the 19th century, philosophy has predominantly relied on science (rather than on religion) as the main source of the knowledge that is to be unified.
After the failure of logical positivism and the mechanistic view of science, only one approach has made a serious claim that it would be able to bring back integration: the General Systems Theory (von Bertalanffy; Boulding). Systems theorists have argued that however complex or diverse the world that we experience, we will always find different types of organization in it, and such organization can be described by principles which are independent from the specific domain at which we are looking. Hence, if we would uncover those general laws, we would be able to analyse and solve problems in any domain, pertaining to any type of system.
Many of the concepts used by system theorists came from the closely related approach of cybernetics: information, control, feedback, communication... In fact cybernetics and systems theory study essentially the same problem, that of organization independent of the substrate in which it is embodied. Insofar as it is meaningful to make a distinction between the two approaches, we might say that systems theory has focused more on the structure of systems and their models, whereas cybernetics has focused more on how systems function, that is to say how they control their actions, how they communicate with other systems or with their own components, ... Since structure and function of a system cannot be understood in separation, it is clear that cybernetics and systems theory should be viewed as two facets of a single approach. In order to simplify expressions, we will from now on use the term "cybernetics" to denote the global domain of "cybernetics and general systems theory". If you prefer, you may substitute "systemic" or "systems scientist" each time you will read "cybernetic" or "cybernetician".
What is the reason that cybernetics does not seem to get the popularity it deserves? What distinguishes cyberneticians from researchers in the previously mentioned areas is that the former stubbornly stick to their objective of building general, domain-independent theories, whereas the latter focus on very specific applications: expert systems, psychotherapy, thermodynamics, pattern recognition, ... These applications attract attention insofar that they are useful, concrete or spectacular. On the other hand, the aim of general integration remains too abstract, and is not sufficiently successful to be really appreciated.
But why then is cybernetics less successful than these more trendy approaches? Clearly the problem of building a global theory is much more complex than any of the more down-to-earth goals of the fashionable approaches. But we may also say that the generality of the approach is dangerous in itself if it leads to remaining stuck in abstractions, which are so far removed from the everyday world that it is difficult to use them, interact with them, test them on concrete problems, in other words, get a feel on how they behave and what are their strengths and weaknesses.
Our contention here is that the goal of global integration is still, if not more, of an essential importance, but that cybernetics has a number of lessons to learn from its more specialised applications. Whereas cybernetics aims to unify science, it is in itself not unified. Instead of looking down on practical applications, it should try to understand how those applications can help cyberneticians in their task of unifying science, and first of all unifying cybernetics. It should look upon them as tools, that can be used for tasks that may extend much further than the ones they were originally designed for.
Where the theory of cybernetics can be enriched by its applications, we may similarly expect that the applications will be enriched by a closer contact with the general theory from which they originated. There is now already a trend in many of those fashionable approaches such as expert systems design, robotics, man-machine communication, etc., to acknowledge the limitations of their specific paradigm, and to look back to a broader, "cybernetical" framework for inspiration on how to overcome them. In conclusion, what we are arguing for is a cross-fertilization between cybernetics and its various recently fashionable applications.
The reason we believe that the time is ripe for such an approach is that both cybernetics and its applications have reached a sufficient level of maturity that it seems realistic to integrate them in practice. The present situation in cybernetics may be compared with the situation in Mathematics at the end of the previous century. What cybernetics needs is support for coping with the practical complexity of its problem domain, and a concrete filling in of some of the main "slots" in its empty framework. What the applications need is a framework in which they can be fitted, brought into contact, and situated the one with respect to the other. This should bring cybernetics back into contact with reality, and help it to succeed in its overall goal of integrating the different systems of thought.
One had to wait further for the classical work of Russell and Whitehead, the Principia Mathematica, in which they ground the "principles of mathematical thinking" in a clear, apparently consistent and complete way. (the theorem of Gö;del later shattered the hope that such a formal treatment could ever be considered complete, but that is another story). What was novel in the work of Russell and Whitehead was that they applied mathematical methods to the foundation of mathematics itself, formulating the laws of thought governing mathematical reasoning by means of mathematical axioms, theorems and proofs. This proved highly successful, and the Principia Mathematica stills forms the basis of the "modern" mathematics as it is taught in schools and universities.
Let us further indicate the similarities and differences between a Principia Mathematica and a Principia Cybernetica. Both mathematics and cybernetics are in the first place metadisciplines: they do not describe concrete objects or specific parts of the world; they describe abstract structures and processes that can be used to understand and model the world. In other words they consist of models about how to build and use models: metamodels (Van Gigh, 1986). This meta-theoretical point of view is emphasized in particular in the so-called "second order cybernetics" (von Foerster, 1979; 1981), which studies how observers construct models.
It is because of this metatheoretic character that mathematics and cybernetics can be applied to themselves: a metamodel is still a model, and hence it can be modelled by other metamodels, including itself (Heylighen, 1988). In mathematics, the most well-known example of such a self-representation is the technique of "Gödelization", where a proposition about natural numbers is represented by a natural number. Of course, it is well-known that any self-representation must be incomplete (LÖfgren, 1990), as illustrated by the Gödel theorem, but we do not consider completeness in the formal sense to be a necessary condition for a practically functioning modelling framework.
Let us proceed with the differences between cybernetics and mathematics. Mathematics is characterized by the following assumptions: simplicity, regularity and invariance; the separability of systems into independent elements; and the objective, context-independent, value-free character of knowledge. Cybernetics, on the other hand, emphasizes complexity, variety and process; the fact that elements always interact; and the subjective, context- and value-dependent nature of knowledge. Cybernetics does not deny the value of mathematics; it assumes it but goes beyond it, by trying to encompass phenomena which cannot be represented in a static, unambiguous, formal framework. It is clear then that the self-application of cybernetics, in the form of a Principia Cybernetica, must be different from the Principia Mathematica model. A Principia Cybernetica must put the emphasis on evolution and open-endedness, on different levels of precision or vagueness, on dynamic interactions between a variety of systems or viewpoints.
Part of the reason why the General Systems movement in the fifties and sixties did not succeed in its objectives was because its models and methods were still too dependent on the static, atomistic paradigm that gave birth to mathematics and classical mechanics. The reason why the present situation is much more promising is that now we dispose of better concepts, tools (e.g. computers), and methods for modelling complex and dynamic phenomena (Heylighen, 1989).
Yet the idea of developing general principles (Principia) still assumes a striving towards clarity, "objectivity", and invariance. We do not want to get trapped in endless discussions and confusions over subjective meanings and viewpoints. The invariant principles that are to be derived, however, will be situated at such a high level of abstraction that they do not impose any absolute restrictions on concrete questions. They will form an empty skeleton or framework on which a multiplicity of more concrete theories can be hung (cf. Boulding, 1956). This framework will function primarily as a heuristic tool for building models, which will not preclude any model, but which will provide guidelines for avoiding difficulties and for making models more adequate. In order to succeed in that, the framework will need to incorporate methods for concretizing its own recommendations, depending on the context of the problem. This means that, unlike mathematics, the framework should provide many intermediate levels between the abstract, precise and invariant principles and their concrete, context-dependent implementations.
The potential for computer technology to revolutionize knowledge systems is of course not only well known, but also well underway. There are many \cite{BUV45,END63,NET65} who have championed the above ideas into the idea of constructing a "universal knowledge system" which would not only dynamically represent the current state of knowledge, but also make it accessible at multiple levels of resolution and in multiple orderings. Such a system is envisioned to have: universal access to all individuals and groups; universal content of all representable knowledge; unlimited "collaborative granularity" to group people and groups of people into other groups of people; a completely connected architecture, to ensure accessibility of the whole system; complete flexibility of representational form and modality; and a maximal interface through human sense organs and effectors, perhaps to the point of neural interfacing.
Of course, such a goal is still quite remote, for those researchers or any others in any field. Yet where else but in Cybernetics and Systems Science should this be seriously attempted? Where else are the fundamental principles of information systems so well understood and developed? Where else is this intimate relation between people and machines more highly championed? And, what other field could most benefit from the possibility of an easing of the construction of a unified conceptual territory from a vast, heterogeneous expanse?
| Synopsys: |
This is the quick answer to this fundamental question. In order to start giving the long answer, we should first examine each of the key terms in this sentence:
Fitness is the most important and tricky term of the answer to define. It can only be defined in terms which are not obvious themselves, and so need further definitions, and so on. One can hope that after a few rounds of definitions, the meaning will become sufficiently intuitive to be satisfactory for most readers. The whole of Principia Cybernetica Web can be viewed as an attempt to provide a sufficiently extensive semantic networks of concepts clarifying concepts (such as "fitness").
"Self-actualization", Maslow's term for maximally developing all our protentialities, and thus reaching the highest level of psychological health and awareness, is merely the implementation of fitness increase in the mental domain (see my paper on Maslow). Similarly, it can be argued that happiness is a direct sign that we have managed to improve our fitness. Thus, if people say that the meaning of life is to "learn and develop", "actualize our potentialities", "improve the balance of pleasure and pain", "enjoy ourselves" or "simply be happy", they are expressing a more limited version of the answer above (limited in the sense that it is more difficult to apply to non-human life, and does not take into account other aspects of life).
On the other hand, people who express the belief that the meaning of life is to "love and be loved", or "promote cooperation and togetherness" are expressing the importance of our social needs, which are another component of fitness. Indeed, fitness for individuals requires fitness for the group to which these individuals belong, and this implies cooperation and "love" rather than selfishness and hostility.
Even those people who state that "life has no meaning" do not contradict the present definition. Indeed, if "meaning" is seen in the restricted sense of a fixed, external purpose, then life has no meaning. "Increasing fitness" is not a goal explicitly imposed by some God, but rather the "implicit goal" governing all of evolution. There are an infinite number of ways in which fitness can be increased, so we cannot say that life necessarily has to move to one end state rather than another. Most changes are initially blind. It is just that some directions (those that decrease fitness) are likely to be eliminated sooner or later by selection.
We remain free in choosing which of the directions we will take: goals or values are not imposed on us. The fitness criterion is merely a guideline to help us choose those most likely to prolong and develop life. But the final decision will depend on our our personal circumstances, and therefore requires reflection. In that sense, the present answer also encompasses the answers of those people who state that the meaning of life is "a personal choice", "to be found within oneself", or even "to ask the question 'What is the meaning of life?'".
The Net's Meaning of Life
Meaning of Life submissions
the meaning of life in the Yahoo subject index
Meaning of life: a large collection of definitions
The Principia Cybernetica project was conceived by Valentin Turchin, a physicist, computer scientist, and cybernetician, whose political activity and antitotalitarian views led to his forced emigration from the Soviet Union to the United States in 1977. He had developed a cybernetic philosophy based on the concept of the "metasystem transition" with implications for human evolution, political systems, and the foundations of mathematics. He further wanted to develop an integrated philosophical system with a hierarchical organization, and involving multiple authors.
In 1987, Turchin came into contact with Cliff Joslyn, a systems theorist, software engineer, and proponent of Turchin's philosophy. After discussing Turchin's ideas for a collaboratively developed philosophical system, Joslyn suggested a semantic network structure using hypertext, electronic mail, and electronic publishing technologies as a viable strategy for implementation, maintenance, and production of such an ambitious project. Together they founded the Principia Cybernetica Project and formed its first Editorial Board. They wrote a first general proposal, and a document they called "The Cybernetic Manifesto" in which the fundamental philosophical positions were outlined. Joslyn began publicizing Principia Cybernetica by posting the relevant documents on the CYBSYS-L electronic mailing list in the autumn of 1989.
This generated a fair amount of response, including that of Francis Heylighen, a physicist, cognitive scientist, and systems theorist. He reacted with detailed comments on the content of the Project (the evolutionary philosophy), its form (the hypermedia organization of knowledge), and the link between the two. Heylighen had been developing a very similar philosophy to Turchin's and had been thinking along the same lines of creating a network of people interested in the domain of complex, evolving systems who would communicate with the help of various electronic media. He started an active correspondence with Turchin and Joslyn, and finally joined them as the third member of the editorial board in spring 1990.
Other reactions to Principia Cybernetica were more contentious. The strong tone of the "Manifesto", which was intended to provoke reaction, engendered a sometimes heated debate on the CYBSYS-L list, where several fundamental criticisms were made, leading the PCP-editors to carefully evaluate the wording of the project. The Manifesto became the first of many publications devoted to PCP, written by the editors and other contributors.
The first official activity of PCP was the sponsorship of a forum on Cybernetics and Human Values at the 8th Congress of the World Organization of Systems and Cybernetics at Hunter College in New York in July of 1990. The Editorial Board were joined by B. Lichtenstein and D. White in a forum which introduced PCP and discussed many of the relevant issues.
Following this forum the editors not only forged coherent working relationships, but were able to come to considerable consensus not only about issues of philosophical content, but also of management and organization.
The publication of the Principia Cybernetica Newsletter # 0 followed, which was widely distributed to members of the cybernetics and systems community by postal mail and computer networks. The Newsletter garnered many favorable and some critical responses from our colleagues, and the Editors proceeded to organize the 1st Principia Cybernetica Workshop, held at the Free University of Brussels during 5 days in July, 1991. This gathering was very successful and well attended, resulting in the publication of the Workbook containing extended abstracts of the papers presented at that meeting; and the Newsletter # 1.
1991 also saw the establishment of the PRNCYB-L electronic mailing list. PRNCYB-L is now used as a discussion medium for over 100 project participants.
National Fund for Scientific Research": one in 1992 for a collective project on Knowledge Development, one in 1993 for the individual project of F. Heylighen devoted to the network support for PCP, and another one in 1994, extending the previous project on Knowledge Development. The latter grant included a contract for a full-time research assistant to support the project. That position was given to Johan Bollen, who started to work for PCP in January 1994. F. Heylighen also received a grant specifically for his PCP-research in 1993 from the "Cultural Support Fund" of the Free University of Brussels. A paper by Heylighen on PCP, entitled "Principles of Systems and Cybernetics", received a "Best Paper Award" for the Symposium on "General Systems Methodology" at the 11th European Meeting on Cybernetics and Systems Research in Vienna, 1992. Following the success of the 1991 Workshop, PCP organized several other conferences, starting with a one-day symposium at the 13th International Congress on Cybernetics in Namur, Belgium in August 1992. A symposium on "Cybernetic Principles of Knowledge Development" was held at the 12th European Meeting on Cybernetics and Systems Research in Vienna, in April 1994 (at the same congress, the Principia Cybernetica Web was publically demonstrated). A very well-attended 3 day Symposium on "The Evolution of Complexity" was organized in Brussels at the "Einstein meets Magritte" conference, in June 1995, and a symposium on "Theories and Metaphors of Cyberspace" was organized in Vienna in April 1996.
1994 was the year in which PCP had been active for five years, leading us to produce a Progress Report. It concluded that, in spite of the great initial ambitions and rather limited means of the project, quite a lot had been achieved. In 1995, a special issue of "World Futures" was published on "The Quantum of Evolution". This collection of invited papers, edited by the PCP board, provided the first extensive overview of the theoretical framework developed by PCP.
In the autumn of 1995, a second electronic mailing list, PCP-news, was installed for the distribution of announcements.
The digest of messages sent to that list provides a detailed account of the developments since then, such as the different "spin-off" groups that PCP helped start up, which include the Global Brain Group, the Journal of Memetics and the study group on Progress.
http://gwis2.circ.gwu.edu/~joslyn/96summer.html for a program of the events). The most important result of the meeting was a new consensual definition of the central concept of "control" together with a number of related concepts. A draft node has already been put on the Web (see below), but it will be elaborated with many more details and related nodes in the coming two months.
It may be of interest to note that a new mailing list, j-memetics, has been created, which is to some degree a "spin-off" of PRNCYB-L. Its aim is to discuss the creation of a peer-reviewed, electronic journal devoted to memetics or "evolutionary models of information transmission". For more info, contact hanss@sepa.tudelft.nl (Hans-Cees Speel) or b.edmonds@mmu.ac.uk (Bruce Edmonds).
Last August, a new study group, associated with PCP, has been started, to discuss the emergence of a "global brain" out of the computer network, which would function as a nervous system for the human "superorganism". Participation is limited to people who have been doing active research and published books or papers on this subject. Present members are: Peter Russell, Gottfried Mayer-Kress, Gregory Stock, Lee Chen, Johan Bollen, Ben Goertzel, Joel de Rosnay, Valentin Turchin and Francis Heylighen. For more info, see http://cleamc11.vub.ac.be/suporgli.html or contact Francis Heylighen.
A first part of the new results, reached during the PCP board meeting in June, on the definition of control have now been incorporated into PCP Web (http://cleamc11.vub.ac.be/control.html). Moreover, our programs for self-organizing hypertext and retrieval of words through spreading activation can now be permanently consulted on the web, via a new node devoted to our research on learning, "brain-like" webs (http://cleamc11.vub.ac.be/learnweb.html).
The PCP editor Cliff Joslyn has moved from Goddard Space Center, NASA, to the Los Alamos National Laboratory. His new address is:
The groups associated with PCP have also been quite active. The people involved with the electronic "Journal of Memetics" have reached consensus on an introductory text describing the aims of the journal, a general editorial policy, a managing editor (Hans-Cees Speel, hanss@sepa.tudelft.nl), and the constitution of an advisory board (presently Daniel Dennett, Aaron Lynch, David Hull and Gary Cziko). At the moment, they are looking for authors wishing to contribute to the first issue, which is scheduled for 1997. If you are interested to write a paper or take part in the reviewing process, please contact Hans-Cees Speel.
The "Global Brain" group (see http://cleamc11.vub.ac.be/gbrain-l.html) has started its discussions on superorganisms and networks playing the role of nervous systems. Thanks again to Bruce Edmonds (who already created the PRNCYB-L archive, and the Journal of Memetics list and web site), an archive of the discussions can now be consulted at http://www.fmb.mmu.ac.uk:80/~majordom/gbrain/
We are happy to announce that Joel de Rosnay is joining PCP as a new "associate" (see http://cleamc1.vub.ac.be/masthead.html). Joel is a systems theorist, futurologist, molecular biologist and prolific writer of popular science books on topics related to the cybernetic world view. He is presently Director of Strategy of the Cite des Sciences et de l'Industrie at La Villette (Paris, France). His book "The Macroscope", a systemic view of the world as whole, will soon be made available on the Web with the support of PCP. Joel is in particular interested in the "cybernetic organism" formed by global society and its "planetary brain" emerging out of the computer networks. His home page, with interviews and excerpts from his work can be found at http://www.cite-sciences.fr/derosnay/e-index.html
The people involved with the electronic "Journal of Memetics", associated with PCP, have set up their (still experimental) web site for the publication of memetics related articles. The first papers should be published in the next few months.
The most important development was the publication on PCP Web of a complete book on the system's approach, "The Macroscope", by PCP associate Joel de Rosnay.
After the very successful Web publication of Joel de Rosnay's book "The Macroscope" (which has drawn many positive responses), we are preparing a Web version of another difficult-to-find classic book on cybernetics and systems thinking: "The Phenomenon of Science. A cybernetic approach to human evolution" by PCP editor Valentin Turchin. The book should be available on PCP Web in the coming weeks.
We are preparing the annual meeting of the Principia Cybernetica Editorial Board (F. Heylighen, C. Joslyn, V. Turchin and J. Bollen) in Brussels. It is likely to take place during the last week of June, and to include a visit to Paris for discussions with PCP associate Joel de Rosnay. It might also be accompanied by a seminar on Metasystem Transition Theory at the Free University of Brussels.
The "Journal of Memetics - Evolutionary Models of Information Transmission", associated with PCP, is ready to go on-line with its first issue. After peer review, four papers and a book review have been accepted for publication. Once the website has been thoroughly tested, its URL will be announced through this and other mailing lists. Richard Dawkins has agreed to join the Journal's advisory board.
As could be expected, there was not much activity during the summer months. As announced earlier, the PCP office has moved to a different building within the Free University of Brussels, and is now housed together with the associated Center Leo Apostel. New phone, fax, mail etc. addresses are listed on PCP's masthead (http://cleamc11.vub.ac.be/MASTHEAD.html). The move of the project's web server to the new physical location, which is connected to the network by a microwave antenna, went surprisingly smoothly. An increase in the number of system crashes after the move seems now to have been solved by updating the network software.
ASSOCIATED GROUPS
The opening up of the mailing list of the Global Brain Group to selected non-members has produced a lot of additional discussions. About a dozen new subscribers with diverse backgrounds have joined the list. The archive of messages can be consulted at http://www.cpm.mmu.ac.uk/~majordom/gbrain/
During a stay in Jan's summer house in the (French) Provence, Jan Bernheim and Francis Heylighen have further developed their ideas for a study group that would focus on an evolutionary analysis of social progress. It starts from the observation that practically all indicators for average quality of life (wealth, life expectancy, level of education, equality, democracy, literacy, IQ, life satisfaction, ...) have undergone a spectacular increase during the last half century. ( see http://cleamc11.vub.ac.be/CLEA/Groups/Progress.html). This undeniable progress for humanity as a whole stands in sharp contrast with the prevailing pessimism of many commentators or the relativism of the postmodernists. The main aim of the group is to analyse these trends critically, and to explain them on the basis of evolutionary principles. This may lead to practical and ethical guidelines for future developments.
This group would be associated with PCP, in a way similar to the "Global Brain Group". This means that the group works on a more specific subject within the larger evolutionary-systemic world view which PCP is developing, thus providing a more specialised focus, while including both PCP members and others. People interested in participating in this study group may contact Francis Heylighen
BOARD MEETING
In the period June 20-30, the annual meeting of the Principia Cybernetica Editorial Board (F. Heylighen, C. Joslyn, V. Turchin and J. Bollen) took place in Brussels. It included a visit to Paris for discussions with PCP associate Joel de Rosnay, and a meeting at the Center Leo Apostel of the Free University of Brussels. The discussions centered on a whole range of issues concerning the organization of the project and its philosophical content. The general state of the project, its web server and associated groups were reviewed.
Some of the practical issues discussed were the editing of nodes by editors at a distance (e.g. using Netscape Gold), and the conversion of LaTeX formatted texts (including a number of PCP papers by Turchin and Joslyn) to HTML. It was decided to try to program a simple converter in Perl, rather than install one of the cumbersome conversion packages that already exist. It was also decided to develop an animated version of the PCP logo, which would illustrate the process of metasystem transition as an infinite recurrence. More advanced interface issues for the organization of Principia Cybernetica Web were discussed, such as the use of frames or Java applets, but no concrete decisions were as yet taken.
At the content level, we focused on the central node about Metasystem Transition Theory, rewriting its text and reorganizing its child nodes. In particular, we decided to add a new "methodology" node. We further discussed different topics, including ethics, the global brain and the idea of progress. Cliff Joslyn proposed a new representation for the central concept of "control", thus extending the one developed at last year's board meeting in Washington DC.
We further discussed a number of recent developments in intelligent computer networking, such as the use of ontologies, semantic webs, link types in hypertext, groupware, multidimensional clustering to develop higher level concepts, graphical representations of complex web structures, agents, and spreading activation. All these technologies are potentially useful to make PCP web more intelligent and user-friendly. Moreover, they are likely to be included in one of the different research proposals being prepared by PCP members and others at the Los Alamos National Research Laboratory, the "Global Brain" study group, and the Free University of Brussels. It was concluded that we need to get a good grasp of the present "state of the art" for these technologies. This will help us to clarify, integrate and strenghten the different proposals.
The meeting with a number of researchers of the Center Leo Apostel (CLEA, see http://cleamc11.vub.ac.be/CLEA/) replaced a planned seminar on Metasystem Transition Theory (MSTT), which was cancelled for practical reasons. The discussion confronted PCP's MSTT with CLEA's research project on transitions between layers of reality. The parallels between both approaches were clear, and it was decided to try and integrate the "control levels" of MSTT and CLEA's "reality layers". This would entail an extension of the known sequence of metasystem transitions down to the level of quantum mechanics, according to the formula: classical mechanics = control (constrained variation) of quantum non-locality. Thus, the hypothesized MST would reduce the infinite dimensional Hilbert space of quantum phenomena to the three dimensional Euclidean space of classical mechanics.
The meeting with Joel de Rosnay at the "Cite des Sciences" in Paris focused mainly on the development of the "Global Brain" theme. de Rosnay suggested to organize a conference on the subject, and to arrange funding for research through various institutions with which he has good contacts. He told us that Microsoft chairman Bill Gates, with whom he is acquainted, expressed particular interest in PCP. We agreed that if de Rosnay does not find a publisher for the English translation of his 1995 book "L'homme symbiotique" (Symbiotic Man), we would publish it on PCP web, like we did with his 1975 book "The Macroscope". de Rosnay said he would send us a representation of his own "spiral" model of transitions to higher level of complexity, for inclusion in PCP web.
ASSOCIATED GROUPS
In the last week of May, the "Journal of Memetics - Evolutionary Models of Information Transmission", associated with PCP, went on-line with its first issue (
The "Global Brain" study group has decided to open up its mailing list to selected subscribers ( see http://cleamc11.vub.ac.be/gbrain-l.html ). The reason is that the founding members were too busy and their number was too small to sustain active discussions. However, since the global brain topic is bound to attract many mudheads and crackpots, while we wish to keep the intellectual level and signal-to-noise ratio of the discussion high, we agreed about a selection procedure on the basis of the submissions of prospective new members.
Alex Riegler, an Austrian cognitive scientist, has applied for a postdoctoral visiting fellowship at the Brussels office of PCP. If the application is accepted by the funding agency, he will start to work here on Feb. 1 for a period of one year (and possibly longer). Alex has been doing research on cognitive constructivism and the systems theory of evolution, applied to the design of autonomous agents. For further details and publications about this quite interesting work, see his home page: http://www.ifi.unizh.ch/~riegler/
Valentin Turchin's book "The Phenomenon of Science" has finally been completely scanned in. (the work was delayed because An Vranckx, who was working on the scanning, has been abroad for several months). Once the text has been converted to HTML and integrated with all the figures, the book will be made available on PCP web. We hope to make the official announcement within the next few days.
The study group on "Progress" associated with PCP has had its first informal meeting in Brussels, just before a seminar on "Understanding Happiness" by Ruut Veenhoven, a Dutch sociologist who has done extensive research on the social, economic and psychological factors involved in life-satisfaction. (see his World Database of Happiness:
VARIOUS ACTIVITIES
In spite of the intervening holidays, November and December were quite busy months for the PCP team. PCP editor Val Turchin's book "The Phenomenon of Science" was finally published on the web, and attracted quite some interest.
Two meetings were announced, a "Symposium on Memetics" (http://cleamc11.vub.ac.be/MEMETSY.html) chaired by PCP editor F. Heylighen and PRNCYB member Mario Vaneechoutte, and a Special Session on "Semiotics of Autonomous Information Systems" (
Although not officially associated with PCP, it is worth mentioning the creation of the new "Journal of Complex Systems" (
It has now been confirmed that Alex Riegler, an Austrian cognitive scientist, will come to work at the Brussels PCP office in February. Although his application to the Belgian Fund for Scientific Research was not accepted, he managed to get money for a year's stay from the Austrian National Bank.
The study group on "Progress", associated with PCP has submitted a research project entitled "Progress in global quality of life and its indicators: an interdisciplinary approach" for funding. The aim is to analyse a host of statistical data in order to study in how far the on-going development and modernization of society is associated with increase in happiness, and thus to test the evolutionary theory underlying PCP in the domain most relevant to our present situation. If the project is accepted, this will add another researcher to the PCP team in Brussels, and provide us with some more money. The promoters of the project are Francis Heylighen, Jan Bernheim, Ruut Veenhoven and Robert Scott Gassler.
THE PRINCIPIA CYBERNETICA WEB
The last part of 1997 was quite unlucky for PCP's technical infrastructure. First, the PRNCYB-L mailing list in Binghamton, NY, broke down for several weeks. Then, the PRNCYB-L archive in Manchester, UK, suffered a disk crash, so that several messages got lost. Finally, on Dec. 5, the main PCP web server in Brussels, Belgium, had a hard disk crash, caused by an electricity cut-off. Because of poor backing-up procedures (which will be remedied soon), the most recent copy of the material we had was 6 months old, so that lots of files were missing.
Happily, a call for help to this mailing list produced a deluge of reactions from people who had kept copies of PCP files. Two of them even had used a web robot to gather a complete copy of PCP web, which was not more than two weeks old. This allowed us to restore all lost files, though the robot produced a number of small formatting changes, which had to be undone. Because of that, you may still find a few errors in URL's in different PCP nodes. Please let us know if you find one, so that we can correct everything.
Thanks again to all those who offered their help. Because of you, PCP web could be restored with a minimum of delay. Your massive response showed how PCP has gathered a wide audience of people actively interested in our project. This group continues to grow, as shown by the 3 to 4 new subscribers this mailing list gains every week (while very few people ever unsubscribe), and by the many email reactions we receive.
It seems that the number of people actively interested grows more quickly than the number of hits on our server (at present inching towards 8000/day). This is probably caused by the massive increase in servers and web pages on the net, which compete for the attention of a more slowly increasing number of web surfers. The result is that the new users PCP web attracts will be lower in number, but higher in their interest for the specific PCP themes. When PCP web was created, there were only some 200 servers in existence, and practically every server was interesting for those exploring the new medium. Nowadays there is such an overkill in available information, that only those really motivated to study cybernetic philosophy are likely to discover, and do the effort to explore, PCP web.
After the busy activities at the end of 1997, the beginning of 1998 was relatively quiet. Alex Riegler has started to work at the Brussels PCP office at the end of January. He has joined the project as an editorial assistant. The new address of his home page is http://cleamc11.vub.ac.be/riegler/ He has also submitted a research project on "Evolutionary Complexification of Knowledge Systems". If this application is accepted, he will get a 3 year postdoc research contract to work with us.
Contributions for two PCP co-organized sessions are being collected. (see http://cleamc11.vub.ac.be/act.html) If you consider submitting an abstract to the symposium on memetics (http://cleamc11.vub.ac.be/MEMETSY.html), let me remind you that the deadline for submission is March 10, that is, next week. (the deadline for the session on Semiotics of Autonomous Information Systems has already passed).
Some of you may remember the symposium on "The Evolution of Complexity", organized by PCP in 1995 in Brussels (see http://cleamc11.vub.ac.be/EINMAGSY.html). The most important papers presented at this symposium, plus a few other selected papers, have been bundled into a book. This volume (the "violet book" in the 8 volume series Proceedings of the interdisciplinary conference "Einstein meets Magritte", see http://cleamc11.vub.ac.be/CLEA/publications.html) has finally been typeset, and proofs have been sent for correction to the authors. This means that in a few months, it should be available from the publisher, Kluwer Academic.
Since we regularly get questions about the existence of study programs in the domain of cybernetics and systems, it seems worth noting the organization of the 5th European School of Systems Science, in Neuchatel, Switzerland, Sept. 7-11, 1998 (see
The editorial board of the Principia Cybernetica Project has been preparing its annual board meeting, which will take place this year in Santa Fe, New Mexico, around August 10-20. This meeting will take place together with an informal, invited workshop involving, in addition to the PCP board, some people from the Santa Fe Institute, Los Alamos National Laboratory and the New Mexico State University. The topic is "Emergent Semantic and Computational Processes in Distributed Information Systems" (see
The Brussels PCP group has received an extensive visit by Mark Bickhard, a cognitive scientist/philosopher/psychologist from Lehigh University, where he has been working with the recently deceased Donald T. Campbell, a PCP associate. Bickhard has developed a philosophy very close to the one we call "Metasystem Transition Theory". Starting from a process ontology, Bickhard develops the theme of variation and selection and emergent organization at the different levels of reality, from quantum fields, via crystals, to living organisms and knowledge, with a specific emphasis on persons. His "interactivist" theory of representation is very close to our view of knowledge based on models, where correspondence is replaced by construction, constrained by selection on the basis of predictions. Bickhard is likely to join the project as an "associate". More info about his work is available at his home page:
The full program of the symposium on memetics, organized by PCP and the Journal of Memetics, including the abstracts of all accepted contributions is now available on the web: http://cleamc11.vub.ac.be/MEMETSY.html. Some 23 contributions have been selected for presentation.
The Brussels PCP group has received another extensive visit, this time by Liane Gabora, an artificial life/memetics researcher from UCLA, and member of the editorial board of the Journal of Memetics. There is a good chance that she will join us to do research at the Center "Leo Apostel" (CLEA) on the emergence of culture during evolution. Liane has developed an "autocatalytic" model for the emergence of culture or thought, inspired by Stuart Kauffman's work on the origin of life and sparse distributed memory models of cognition. This fits in both with PCP's theory of metasystem transitions, and CLEA's project on "transitions between hard and soft layers of reality". More info on her work can be found at http://cleamc11.vub.ac.be/CLEA/seminars/Gabora.txt . A recent paper is available at
Most papers to be presented at the symposium on memetics, organized by PCP and the Journal of Memetics, are now available on the web: http://cleamc11.vub.ac.be/MEMETSY.html. The symposium will take place for two and a half days, from August 26 (afternoon) to August 28. The latest issue (June) of the Journal of Memetics has been published at http://www.cpm.mmu.ac.uk/jom-emit/1998/vol2/index.html
The project on progress in global quality of life which we submitted was unfortunately not accepted by the funding agency. Neither was Alex Riegler's application for a 3 year Postdoc research contract at CLEA. We'll have to try again next year, or find alternative sources of funding. Johan Bollen has carried out extensive psychological experiments, in collaboration with people from the Catholic University of Leuven, to test the basic assumptions that underly our "learning web" methodology (http://cleamc11.vub.ac.be/LEARNWEB.html). At first sights, the results seem positive, but the data need much further processing.
After a year of relatively low level activity, the discussions on our PRNCYB-L mailing list have become very intensive again. Especially the topics of "non-physical experience", "mind and body", "reductionism, holism and complexity" and "will and free will" have produced dozens of messages each. John J. Kineman is presently exploring the possibility to create a two-way gateway between the PRNCYB-L emailing list, and a HyperNews discussion system on the web, that could be used also by non-PRNCYB subscribers. HyperNews was originally developed by another PRNCYB member, Daniel LaLiberte. You can try out a first prototype at
PCP has had had a successfull annual meeting of the editorial board in
Santa Fe, New Mexico, in which outstanding issues were discussed, and
contacts were made with different researchers working in New Mexico.
The meeting was organized together with a workshop on
"Emergent Semantic and Computational Processes in Distributed Information
Systems" at the Los Alamos National Laboratory (LANL), in which all PCP
visitors and local residents participated, together with a number of
researchers from LANL, the Santa Fe Institute (SFI), and New Mexico State
University (NMSU). The workshop was well attended and aroused quite some
interest and discussion about the newly emerging domain of
self-organization and complexity models applied to information networks,
such as the web.
Texts of the contributions are being collected, and will be gradually made
available on the workshop's website
(
In addition, the PCP group had several interesting discussions with
researchers working in the New Mexico area, including Norman Johnson, the
driving force behing the LANL "Symbiotic Intelligence Project"
(
Liane confirmed that she has accepted our invitation to come to work in
Brussels on a two year research contract, starting on Oct. 1. This will
allow her to finish her PhD and continue her research on the emergence of
culture, while collaborating with the Brussels PCP group at the Center "Leo
Apostel". Inversely, a possibility was discussed for Johan Bollen from the
Brussels group to come and work at LANL for a one year period, in order to
collaborate more closely with Luis Rocha and Cliff Joslyn, the
representatives of PCP in New Mexico. Other possibilities for collaboration
were discussed with Bonabeau and Johnson, although no concrete decisions
have been made as yet.
Because of these different side-activities, together with the not-to-be
missed opportunities for sight-seeing and hiking in the spectacular New
Mexico surroundings, we had perhaps not as much time for the board meeting
itself as we had hoped. In particular, we did not manage to have in-depth
discussions on fundamental theoretical issues, although we did discuss some
interesting implications of the emergence of collective intelligence in
animal and human societies for developing a more detailed model of large
scale metasystem transitions. On the other hand, the meeting concluded with
a long list of concrete plans for the further development of the project
organization in general, and PCP web in particular. These objectives are
summarized below.
On the organizational level, it was decided to create an American office
for the project ("PCP West"), to complement the present European office in
Brussels. This permanent PCP presence at LANL has been made possible by the
recent promotion of PCP editor Cliff Joslyn to a tenured "staff" position
at the Los Alamos lab. The PCP editorial assistants, Johan Bollen and Alex
Riegler, were formally 'promoted' to "assistant editors". We also
reiterated our aim to more closely involve the different "associates" of
the project in the writing of nodes, and suggested some names of new people
to invite as associates or authors of nodes. Finally, we decided to renew
contacts with the International Society for Systems Science, which through
Bela A. Banathy expressed their interest to collaborate with PCP.
PLANS FOR PCP-WEB
During the meeting we received a final confirmation from Mick Ashby,
grandson of the famous cybernetician W. Ross Ashby, that he had received
permission from the publishers of his grandfather's classic book,
"Introduction to Cybernetics", to publish the book in an electronic version
on PCP Web. Since this will be the third "out of print" book which we
republish on the Web, we decided to create a special "library" section on
PCP web, with electronic versions of important books. The Ashby book will
be scanned in during the coming weeks and converted to PDF and HTML for
easy printing and browsing.
Moreover, we decided to produce an easy-to-print "book" version of all PCP
nodes, so that people don't need to browse between the hundreds of nodes,
but can read a more or less complete version of PCP web on paper. A more
ambitious aim, which may not be realized soon, is to provide PCP web users
with a "shopping basket", in which they can gather a list of only those
nodes ("pages") they are interested in, and then receive all these nodes at
once in an easy-to-print file format, without the navigational formatting
(menu bar, child nodes, etc.) that is only useful for web browsing.
PCP web itself is scheduled for a major overhaul, to improve both its
organization and its appearance, so that it would become more easy to
browse and to edit. Structurally, the idea is to clearly distinguish all
database fields (author, date, title, content, etc.) within the HTML code,
by introducing new tags such as
We have been experimenting with a number of new layouts, which should be
both esthetically pleasing and help the user to navigate more efficiently.
We would be curious to hear your reactions and suggestions with respect to
these different options. Some trial layouts can be seen at the subsequent
URLs http://cleamc11.vub.ac.be/layout/Default1.html, ..., Default12.html.
Apart from purely esthetical issues such as color schemes, icons and logos,
the main issue is whether we should put the navigational structure of
parent ("up") and child ("down") nodes in a vertical side bar (e.g
http://cleamc11.vub.ac.be/layout/Default7.html), or in a horizontal box at
the bottom of the page (e.g.
http://cleamc11.vub.ac.be/layout/Default12.html). Please let us know which
features or layouts you prefer.
For PCP web as a whole, it was decided to create, together with the New
Mexico office, a New Mexico mirror of the main Brussels server, so as to
facilitate access from America and provide a permanently available backup
in case of server problems. Moreover, if a NSF proposal submitted by the
LANL group and a group at NMSU would be accepted, money would become
available to create a "collaborative knowledge space", at NMSU. This would
contain an experimental version of PCP Web, the SFI web and perhaps others,
so as to allow experiments with different algorithms for web
self-organization or information retrieval, as they were developed by Luis
Rocha, Johan Bollen and other PCP contributors. It was also decided to try
and reserve some alternative domain names for the PCP server(s), in
particular: pcp.vub.ac.be, pcp.lanl.gov and cybernetica.org (pcp.org,
pcp.com and pcp.net are already taken by organizations that have nothing to
do with Principia Cybernetica).
MEMETICS SYMPOSIUM IN NAMUR
The Brussels PCP people had hardly recovered from the jetlag of the journey
back to Europe, or we had to go to the 3-yearly Cybernetics congress in
Namur, Belgium, for the first ever symposium on Memetics. The symposium was
organized and chaired by Mario Vaneechoutte and myself. It was quite
successful, with attendance ranging between 15 and 40 people during the two
and a half days. The discussions after each talk were particularly
animated, showing that memetics has developed into a topic that receives a
lot of interest, especially among young researchers. The average age of the
contributors was quite low (most of them did not have a PhD yet), and about
a generation younger than the age of the attendant to other symposia. The
congress president, Jean Ramaekers, told me that he was very happy with
this "rejuvenation" of a congress that has taken place without interruption
since 1956.
By the way, Jean Ramaekers and me also discussed the possibility to create
a Belgian association for cybernetics and systems science. This informal
association, for which WOSC president Robert Vallee suggested the name
"Systemica Belgica", would be used as a communication channel between
researchers in Belgium, to inform each other about cybernetics related
activities, such as seminars, conferences, projects, etc. If you work in or
around Belgium and would be interested to participate, please send me a
message with your address, domain of interest and suggestions about the
organization.
From the scheduled symposium program
(http://cleamc11.vub.ac.be/MEMETSY.html), only 3 contributors did not make
it: Liane Gabora, who had apologized because she was too busy preparing her
long term visit to Belgium, Thomas Quinn and Koen Bruynseels. On the other
hand, a guy whose name I don't remember (?Rosdeitcher?) presented an
improvised, but entertaining talk in which he sketched his own "conversion"
from being a follower of Ayn Rand's "objectivist" philosophy to becoming an
advocate of the memetic/cybernetic paradigm.
From the other, scheduled talks, I particularly appreciated my co-chair
Mario Vaneechoutte's speculations on the origin of life as a model for
memetics, Michael Best's simulation of cultural vs. genetic evolution,
Szabolcs Szamado's analysis of fundamental memetic replication processes,
John Evers' application of memetics to explain altruism and Paul Marsden's
review of research on "social contagion" as an existing body of empirical
data that cries out for a memetic reinterpretation. The talk by my PCP
collaborator Johan Bollen about our learning web algorithms also generated
a very positive response, although I am of course not in an objective
position to judge about its quality (;-). Practically all papers should by
now be available on the web via the above symposium URL. They will be
published by the end of this year as part of the congress proceedings.
The symposium was concluded with a lively panel discussion, chaired by Gary
Boyd, in which the absent panel member Gabora was replaced by Paul Marsden,
and a short brain storming session with all remaining participants to
generate a list of suggestions for us to advance the field of memetics. One
of the concrete decisions was to steer the Journal of Memetics more in the
direction of the system of commentary used by "Behavioral and Brain
Sciences". This requires us setting up a list of commentators.
We have a lot of it to thank to the World-Wide Web system becoming available in the meantime, solving most of our technical problems. We certainly must give credit to Cliff Joslyn for so well anticipating a system which at that moment did not exist, except in the mind of its inceptor, Tim Berners-Lee, who wrote his first, privately circulated, proposal for WWW at about the same time.
We will now review each goal separately, by quoting each of the 12 points from the original document, noting "YES" it it has been achieved, "NO" if we aren't there yet, and "MAYBE" if it has been achieved partially.
1. For a group of researchers, perhaps not all geographically close, to collaboratively develop a system of philosophy, where philosophy is taken in the general sense of clear and consistent language about ideas and concepts
The overall score seems pretty impressive: if we give 1 for a YES, 0 for a NO and 0.5 for a MAYBE, we get 9 out of 13, that is: 69 %, after less than 5 years of development.
Note, however, that these are objectives mostly about the "form" or organization of the Project. The goals for the "content" or philosophy were never stated as explicitly, apart from building a "complete and consistent philosophical system", including metaphysics, epistemology and ethics. Our system is definitely not complete, though its reach is quite broad, and few fundamental issues are left untouched. Its consistency is debatable but there are no obvious contradictions.
Taking into account that the original proposal described PCP as a "very long term" project, we may conclude that there is reason to be proud of what we have achieved in a rather short term existence.
Philosophy is the putting of our thought and language in order.
Philosophy is important. Philosophy is a part of our knowledge.
Cybernetic epistemology defines knowledge as
the existence in a cybernetic system of a model of some part of reality
as it is perceived by the system. A model is a
recursive generator of predictions about the world
which allow the cybernetic system to make decisions about its actions.
The notions of meaning and truth must be defined
from this perspective.
Knowledge is both objective and subjective because it
results from the interaction of the subject (the cybernetic system)
and the object (its environment). Knowledge about an object is
always relative: it exists only as a part of a certain subject.
We can study the relation between knowledge and reality (is the
knowledge true or false, first of all); then the subject of
knowledge becomes, in its turn, an object for another subject
of knowledge. But knowledge in any form (a proposition,
a prediction, a law), irrespective of any subject is a logical absurdity.
A detailed development of cybernetic epistemology on the basis
of these definitions is critical for the
formalization of the natural science and natural philosophy, and the
interpretation of mathematical systems.
Cybernetic metaphysics asserts that freedom is a fundamental
property of things. Natural laws act as constraints on that freedom;
they do not necessarily determine a course of events.
This notion of freedom implies the existence of an agency,
or agencies, that resolve the indeterminacy implicit in freedom
by choosing one of the possible actions.
Such an agency is defined as a will. A will exercises control over a system
when the freedom of that system is constrained by actions
chosen by the will.
We understand God in the spirit of pantheism.
God is the highest level of control in the Universe.
God is for the Universe what human will is for human body.
Natural laws are one of the manifestations of God's will.
Another manifestation is the evolution of the Universe: the Evolution.
When a number of systems become integrated so that a new level of
control emerges, we say that a metasystem has formed. We refer to
this process as a metasystem transition.
A metasystem transition is, by definition, a creative act.
It cannot be solely directed by the internal structure or logic of a system,
but must always comes from outside causes, from "above".
The metasystem transition is the quantum of evolution.
Highly organized systems, including living creatures,
are multilevel hierarchies of control resulting from
metasystem transitions of various scales.
Major evolutionary events are large-scale metasystem transitions
which take place in the framework of the trial-and-error processes
of natural selection.
Examples include: the formation of self-duplicating macromolecules;
formation of multicellular organisms;
emergence of intelligent organisms; formation of human society.
Human intelligence, as distinct from the intelligence of non-human
animals, emerges from a metasystem transition, which is
the organism's ability to control the formation of
associations of mental representations. All of specifically human
intelligence, including imagination, language, self-consciousness,
goal-setting, humor, arts and sciences, can be understood
from this perspective.
The emergence of human intelligence
precipitated a further, currently ongoing, metasystem
transition, which is the integration of people into human societies.
Human societies are qualitatively different from societies of animals
because of the ability of the human being to create (not just use)
language. Language serves two functions: communication between
individuals and modeling of reality. These two functions are,
on the level of social integration, analogous to those of the nervous
system on the level of integration of cells into a multicellular
organism.
Using the material of language, people make new --- symbolic -
models of reality (scientific theories, in particular) such as
never existed as neural models given us by nature.
Language is, as it were, an extension
of the human brain. Moreover, it is a unitary common extension
of the brains of all members of society. It is a collective
model of reality that all members of society labor to improve,
and one that preserves the experience of preceding generations.
We make a strong analogy between societies and neural,
multicellular organisms. The body of a society
is the bodies of all people plus the things made by them.
Its "physiology" is the culture of society. The emergence
of human society marks the appearance
of a new mechanism of Universal Evolution: previously
it was natural selection, now it becomes conscious human
effort. The variation and selection necessary for the increase
of complexity of the organization of matter
now takes place in the human brain; it becomes
inseparable from the willed act of the human being.
This is a turning point in the history of the world:
the era of Reason begins.
The human individual becomes a point of concentration of Cosmic
Creativity. With the new mechanism of evolution, its
rate increases manifold.
Turning to the future we predict that
social integration will continue in two dimensions, which
we can call width and depth. On the one hand (width), the growth of
existing cultures will lead to the formation of a world society and
government, and the ecological unification of the biosphere under human
control. The ethics of cybernetical world-view demands that each of us
act so as
to preserve the species and the ecosystem, and to maximize the potential
for continued integration and evolution.
On the other hand (depth), we foresee the physical integration of
individual people into "human super-beings", which
communicate through the direct connection of their nervous systems.
This is a cybernetic way for an individual human person
to achieve immortality.
The problem of immortality is the problem of
ultimate human values, and vice versa.
Living creatures display a behavior
resulting from having goals. Goals are organized hierarchically,
so that in order to achieve a higher-level goal the system has to
set and achieve a number of lower-level goals (subgoals).
This hierarchy has a top: the
supreme, ultimate goals of a creature's life. In an animal this
top is inborn: the basic instincts of survival and reproduction.
In a human being the top goals can go beyond animal instincts.
The supreme goals, or values, of human life are, in the last analysis,
set by an individual in an act of free choice. This produces the
historic plurality of ethical and religious teachings.
There is, however a common denominator to these teachings:
the will to immortality. The animal is not aware of its
imminent death; the human person is. The human will to immortality
is a natural extension of the animal will for life.
One concept of immortality we find in the traditional
great religions. We designate it as metaphysical.
It is known as immortality of soul, life after death, etc.
The protest against death is used here as a stimulus to accept
the teaching; after all, from the very beginning it promises
immortality. Under the influence of the critical scientific method,
the metaphysical notions of immortality,
once very concrete and appealing, are becoming
increasingly abstract and pale; old religious systems are slowly
but surely losing their influence.
Another concept of immortality can be called creative, or
evolutionary. The idea is that
mortal humans contribute, through their creative acts,
to the ongoing universal and eternal process -- call it Evolution,
or History, or God -- thus surviving their physical destruction.
This uniquely human motive underlies, probably, all
major creative feats of human history.
The successes of science make it possible to raise the banner
of cybernetic immortality. The idea is that the human being
is, in the last analysis, a certain form of organization of
matter. This is a very sophisticated
organization, which includes a high multilevel hierarchy of control.
What we call our soul, or our consciousness, is associated with
the highest level of this control hierarchy. This organization can
survive a partial --- perhaps, even a complete --- change
of the material from which it is built. It is a shame to
die before realizing one hundredth of what you have conceived
and being unable to pass on your experience and intuition.
It is a shame to forget things even though we know how to store
huge amount of information in computers and access them in
split seconds.
Cybernetic integration of humans must preserve
the creative core of human individual, because it is the engine
of evolution. And it must make it immortal, because
for the purpose of evolution there is no sense in killing humans.
In natural selection, the source of change is the mutation
of the gene; nature creates by experimenting on genes and seeing
what kind of a body they produce. Therefore, nature has to
destroy older creations in order to make room for the newer ones.
The mortality of multicellular organisms is
an evolutionary necessity. At the present new stage of evolution,
the evolution of human-made culture, the human brain is
the source of creativity, not an object of experimentation. Its
loss in death is unjustifiable; it is an evolutionary absurdity.
The immortality of human beings is on the agenda of Cosmic Evolution.
The future immortality of the human person does not
imply its frozen constancy. We can understand the situation
by analogy with the preceding level of organization.
Genes are controllers of biological evolution and they are immortal,
as they should be. They do not stay unchanged, however,
but undergo mutations, so that human chromosomes are a far cry
from the chromosomes of primitive viruses.
Cybernetically immortal human persons may mutate and evolve
in interaction with other members of the super-being,
while possibly reproducing themselves
in different materials. Those human persons who will
evolve from us may be as different from us as we are different
from viruses. But the defining principle of the human person
will probably stay fixed, as did the defining principle of the gene.
Should we expect that the whole of humanity will
unite into a single super-human being?
This does not seem likely, if we judge from the history
of evolution. Life grows like a pyramid; its top goes up
while the basis is widening rather than narrowing.
Even though we have seized control
of the biosphere, our bodies make up only a small part of the whole biomass.
The major part of it is still constituted by
unicellular and primitive multicellular organisms, such as plankton.
Realization of cybernetic immortality will certainly require
some sacrifices --- a vehement drive to develop science, to begin with.
It is far from obvious that all people and all communities
will wish to integrate into immortal super-beings.
The will to immortality, as every human feature,
varies widely in human populations. Since the integration we speak about
can only be free, only a part of mankind -- probably a small part -
should be expected to integrate. The rest will continue to exist
in the form of "human plankton".
But it is the integrated part of humanity that will ultimately control
the Universe. Unintegrated humanity will not be able to compete
with the integrated part. This becomes especially clear when
we realize that the whole Cosmos, not the planet Earth,
will be the battlefield. No cosmic role for the human race is possible
without integration. The units that take decisions must be
rewarded for those decisions, otherwise they will never take them.
Can we imagine "human plankton" crowded
in rockets in order to reach a distant star in ten, twenty
or fifty generations? Only integrated immortal creatures
can conquer the outer space.
At present our ideas about the cybernetic integration of humans
are very abstract and vague. This is inevitable; long range
notions and goals may be only abstract. But this does not mean
that they are not relevant to our present concerns and problems.
The concept of cybernetic immortality can give shape to
the supreme goals and values we espouse, even though
present-day people can think realistically only in terms
of creative immortality (although -- who knows?).
The problem of ultimate values is the central problem of our
present society. What should we live for after our basic needs
are so easily satisfied by the modern production system?
What should we see as Good and what as Evil? Where are the ultimate
criteria for judging social organization?
Historically, great civilizations are inseparable
from great religions which gave answers to these questions.
The decline of traditional religions appealing to metaphysical
immortality threatens to degrade modern society.
Cybernetic immortality can take the place
of metaphysical immortality to provide the ultimate goals and values
for the emerging global civilization.
We are living at a time when we can see
the basic contradiction of the constructive evolution of
mankind very clearly: it is the contradiction between human
integration and human
freedom. Integration is an evolutionary necessity. If humanity sets itself
goals which are incompatible with integration the result will be
an evolutionary dead end: further creative development
will become impossible. Then we shall not survive. In the
evolving Universe there is no standstill: all that does not
develop perishes. On the other hand,
freedom is precious for the human being;
it is the essence of life. The creative freedom of individuals is
the fundamental engine of evolution in the era of Reason. If it
is suppressed by integration, as in totalitarianism,
we shall find ourselves again in an
evolutionary dead end. This contradiction is real,
but not insoluble. After all,
the same contradiction has been successfully solved on other
levels of organization in the process of evolution. When cells
integrate into multicellular organisms, they continue to perform
their biological functions--metabolism and fission. The new quality,
the life of the organism, does not appear despite the
biological functions of the individual cells but because of them
and through them. The creative act of free will is
the "biological function" of the human being.
In the integrated super-being it
must be preserved as an inviolable foundation,
and the new qualities must appear through it and because of it.
Thus the fundamental challenge that the humanity faces now
is to achieve an organic synthesis of integration and freedom.
Goguen also opposed the striving towards consensus, which is a fundamental goal of the Principia Cybernetica, on the grounds that all opinions are valuable, and that no one viewpoint should be privileged. This criticism is more difficult to answer in a few words.** It was repeated in different forms by different people, mostly those with a "post-modernist" or "social constructivist" philosophy. These critics stress the relativity of knowledge, and the creativity which arises from a variety of different opinions.
But we hold that this creativity can only appear through a confrontation and conversation between the different opinions, and that is just what Principia Cybernetica proposes. Without at least an attempt to reach consensus, people will stick to their own opinions, and no novelty is created. But it is not our intention to impose a consensus, and we start from the principle that Principia Cybernetica must be open-ended: every new idea or opinion can be incorporated somewhere along the way, even if only as a "discussion node". We do not expect to reach a complete consensus in any foreseeable future. Yet we do hold that there is a deep unity in the ideas characterizing Systems Theory and Cybernetics. In our experience, those with a background in Cybernetics or Systems share these fundamental concepts and values, although they may express them with different words. Further, we hold that a fundamental, broad consensus at the conceptual level is necessary for the advancement of a discipline, or a society.
Other criticisms (albeit in a generally sympathetic spirit) about the philosophy behind Principia Cybernetica, and its practical realizability, were made by Gerard de Zeeuw and Rod Swenson to Heylighen when he presented the ideas of Principia Cybernetica to a number of people at the European Meeting on Cybernetics and Systems in Vienna (April 1990). Swenson mentioned in particular the difficulty of maintaining copyright in a network which is authored collectively by many different people. On the other hand, Principia Cybernetica was enthusiastically welcomed by Gordon Pask, who is one of the main theorists in the "social constructivist" paradigm, and the creator of conversation theory.
Dr. Francis Heylighen et al, Free U. of Brussels
Now this is hypertext! Over 600 documents of profuse hypertext. Several methods of navigating the library, including menus, indexes, and a graphical browser. The subject matter of cybernetics is very closely related to the Web itself.
After the free voting procedure, PCP Web ended up with a "Honorable Mention" for the "
The websmiths are hard at work on this one, using a full bag of HTML
(Hypertext Markup Language) tricks to bring you representational maps of
the Webspace that you can click on, searchable indices, and other goodies.
Choice tidbits include the realtime Web visualizer tools, John December's
comprehensive treatise on computer-mediated communication, the full text of
Darwin's On The Origin Of Species, and fresh news from the Project Xanadu
folks, complete with an impressive bibliography. Start your education on
the tech behind the hype at http://cleamc11.vub.ac.be/.
The following quotations give a good idea of how Principia Cybernetica Web is perceived by others. I have separated "personal" comments (made in various places linking to PCP Web because they find the subject interesting) from "professional reviews" by various web surveying service, which are not a priori interested in the subject, but try to evaluate PCP web for the "general reader" who is unlikely to know anything about cybernetics.
You can
"an excellent resource for cybernetics, systems
theory, and other disciplines often mentioned in Neuro-Linguistic Programming circles" (Neuro-Linguistic Programming and Design Human Engineering
)
"The most impressive Cybernetics resource I've ever seen." (Intelligent Systems
)
"An extraordinarily interesting site about evolution, cybernetics and philosophy." (
"... for easy to understand definitions of cybernetics and virtual reality" (
"an excellent
resource for systems science. " (Jon Wallis' Home
Page)
"The stated goal of the Principia Cybernetica Project is to link all of Mankind's knowledge... have to give them credit for ambition." (
"An intriguing place" (
"Everything you ever wanted to know about systems and cybernetics".(
"congratulations on a job well-done, both in initiating Principia Cybernetica in the first place, and also in implementing the Principia Cybernetica Web, which is a rare and rich site on the Net." (Arkuat's comments on PCP )
"...and finally, the ultimate...
"An extremely sensible philosophy. The next step in human
evolution!" (
" For some theoretical background try [...] the Principia Cybernetica Web which will stretch your mind a little" (
" This is a remarkable site: Systems Science,
Feedback Loops, etc. It's a very busy site, so be patient and keep trying." (
" More than you can ever learn on cybernetics and related issues - the Website is overwhelming! (
"The Principia Cybernetica site is the largest Web 'nexus' on
cybernetics and general systems theory."(
"a fascinating collection of indexes and links on a diverse range of topics collateral to Gestalt and Systems conceptualization" (
"An extraordinary experience of collective creation on
the Web : an international group of research scientists
is writing an hypertext on the global brain created by
the interconnection of men, computers and network.
A quantum leap into the third millenium." (
"Un extraordinario proyecto que
prentende lograr las respuestas a las preguntas fundamentales
del ser humano a traves de la inteligencia artificial."(
"By now the alarm was permanently set at 4:30 am but Timothy Alan Hall never heard it. He had rewired
the little clock radio to activate an ancient reel-to-reel recorder on the other side of the trailer, hooked up
an equally old set of theatre speakers and had it rigged to play his tape recording of a vintage 8086
computer booting up off dual floppies, grinding into first gear with a seriously irritating reminder of days
long gone.[...]
Tim was perfectly aware of the existence of memetic evolution, an obvious competition going on between
genes and memes and his favorite web site was Principia Cybernetica which he studied when time
permitted. The various philosophical subjects and New Agey topics failed to hold his interest for long but
the truth was that memes did exist, were powerfully motivated and his own life had been changing
positively because of them. The truth was inescapable."(
"What can artificial systems tell us about the meaning of life? What are we doing
here anyway? These are some of the questions tackled on the PCP's Web server at
the Free University of Brussels." (
"The cool, the innovative, the excellent - they're all here in our
gallery of Internet resources that exemplify the pioneering spirit of
the Internet. These are the pages we like this week:
December 30, 1994 to January 5, 1995.
Academia:
Cybernetics and Systems Theory" (
"A 3 star site. Rating Summary:
"Content: 41/50,
Presentation: 34/50,
Experience: 35/50
In mathematics, we can mention
Powers
Campbell
Beyond 2nd Order cyb.
Our methodology to build this complete philosophical system is based on a "bootstrapping" principle: the expression of the theory affects its content and meaning, and vice versa. In this way we aim to apply the principles of cybernetics to their own development.
Our philosophy too is based on cybernetic principles. Our epistemology understands knowledge as a model, which is constructed by the subject or group, but undergoes selection by the environment. Our metaphysics asserts actions as ontological primitives. On the basis of this ontology, we define the most important concepts and organize them in a semantic network. At a higher level, we also lay out the fundamental principles of cybernetics in terms of these underlying concepts.
One of the central concepts is that of evolution in the most general sense, which is produced by the mechanism of variation and selection. Another is control, which we define in a special cybernetic sense, and assert as the basic mode of organization in complex systems. This brings us to the central concept for MSTT, that of the metasystem transition, or the process by which control emerges in evolutionary systems.
On this basis we then reconstruct the
complete history of evolution, from the Big
Bang to the present, as a sequence of MST's. An extrapolation of this sequence
provides us with a first glimpse of what the future
might bring. Finally, the possible dangers and opportunities of our evolutionary
future direct our attention to the need for formulating an ethics,
based on evolutionary and systemic principles, that could guide our actions.
Yet, we wish to avoid an
over-formalization of the semantic structures we create. The meaning of a
term will be partially formal, determined by the network of semantic
relations to which it belongs; and partially informal, determined by the
personal interpretation of the user who reads the exposition, and who
tries to understand the concept by making associations with the context.
Such a format allows the adequate representation of precise, mathematical
concepts, of vague, ambiguous, "literary" development, and of the whole
continuum in between. The degree of "formality" can be used to measure the position of a text on that continuum.
Vague or ambiguous concepts can be incrementally refined and clarified through the process of progressive formalization. Formalization may go in rounds, or levels, becoming more intensive and extensive. In keeping with this strategy, nodes we are writing will be initially
organized according to the usual notion of their conceptual dependency
understood informally or semi-formally. As the collection of nodes grows,
we give more time to the work on formal semantics and the structuring of
this accumulated material.
Both semantic networks and progressive formalization avoid starting from a fixed set of primitives or foundational concepts. Instead, we use part of the concepts to clarify other concepts, and vice versa. Thus, by allowing multiple beginnings to exist in parallel we avoid the shortcomings of foundationalism. The resulting system can be read or understood in different orders, for example starting from "meaning" as a primitive concept to develop the concept of evolution, or starting from evolution to analyse the evolution of meaning.
We are well aware of these dangers, but on the other hand we are also aware
of the risk of the converse, of a failure to generate any firm
foundations on which theory can be constructed. We believe that it is this
latter condition that Cybernetics and Systems Science has indeed found itself in today. Even a
cursory examination of current systems literature will reveal a veritable
zoo of advanced, highly sophisticated theories which have only a loose and
metaphorical relation to each other. A clear and elegant underlying theory
on which they could be reconciled is simply lacking.
Rather the approach that we adopt aims to steer a middle ground between
both extremes. It does so through the reliance on the general method we
adopt throughout: a balance between the freedom of variation and the
constraint of selection in a hierarchically organized system of control. In
this case the multiple components of the hierarchy are foundations,
axiomatic sets which reciprocally and irreducibly support each other. While
each component is itself a stable foundation, the overall metasystem is
a-foundational: the choice of an axiom set is ultimately either arbitrary
or non-theoretical (pragmatic).
In this sense, the philosophy we propose is
anti-foundational. Yet a constructive philosophy can be considered
foundational in the sense that it takes the principle of constructive
evolution itself as a foundation. This principle is different from other
foundations, however, because it is empty (anything can be constructed,
natural selection is a tautology), but also because it is situated at a
higher, "meta" level of description. Indeed, constructivism allows us to
interrelate and inter-transform different foundational organizations or
systems, by showing how two different foundational schemes can be
reconstructed from the same, more primitive organization.
Similarly, a metafoundational theory would consist of a set of propositions which can be derived from multiple sets of foundational propositions. Propositions which are primary (axioms) in one system would be derived in another system. No set of fundamental propositions would be absolutely primary. The whole theory should rather be viewed as a bootstrapping (cf. Heylighen's paper on "Knowledge structuring") network, where A derives from B and B derives from A.
A mathematical structure which might possibly express this arrangement is a multiply rooted DAG (Directed Acyclic Graph).
Psychological constructivism asserts that knowledge is constructed by the
subject, and not a simple "reflection" of or correspondence to reality.
Following especially Kant, the neural mechanisms of the sense organs, the
cortex, and the entire brain are seen as active mediators which provide the
inherent "categories of perception". It follows that perception and
knowledge are in fact a model of reality, and not merely a reflection
or impression of it.
We can also describe an extreme version of radical constructivism, which is
currently fashionable with some cyberneticians, but which we reject.
Some radical constructivists approach strong skepticism by denying the existence
of any external reality, and simply define reality as our
knowledge. This "brain in a vat" view is unnecessarily strong. Instead we
take a kind of agnostic view, which is a-realist, not anti-realist.
While it is true that knowledge provides no direct and incorrigible access
to the world, and it is not justified to make strong inferences about
reality on the basis of knowledge, at the same time it is not allowed to
make inferences about reality on the basis of a lack of knowledge:
ignorance of something does not entail its non-existence.
We accept mathematical and psychological constructivism, but we go further.
We call our evolutionary philosophy physically constructive in the
sense that systems can only be understood in terms of the (physical)
processes which manifest them and by which they have been assembled. This is
certainly true for physical and biological systems, but also holds for
formal, symbolic, and semantic systems. In particular, we hold that
semantics, language, and mathematics must always be understood in the
context of the physical basis of their operation---on the physical systems
(e.g. sense organs, brains, machines, computers) which transmit, receive,
and especially interpret physical tokens.
In a traditional systems philosophy "organization" might be seen as the fundamental principle of being, rather than God, matter, or the laws of nature. However it still begs the question where this organization comes from. In our evolutionary-systemic philosophy, on the other hand, the essence is the process through which this organization is created.
Therefore, our ontology starts from elementary actions, rather than from static objects, particles, energy or ideas. These actions are the primitive elements, the building blocks of our vision of reality, and therefore remain undefined. Actions are in not general not deterministic but involve an element of freedom. A sequence of actions constitutes a process. Our ontology is thus related to the process metaphysics of Whitehead and Teilhard de Chardin. Its historical origin can be traced back even further to the development from Kant to Schopenhauer.
Relatively stable "systems" are
constructed by such processes through the mechanism of variation and selection. This leads to the spontaneous emergence of more complex
organizations during evolution: from space-time and elementary
particles, to atoms, molecules, crystals, DNA, cells, plants, animals,
humans, and human society and culture (see the history of evolution). This developmental sequence provides us with a basis for our cosmology. Because of this self-organization of the universe, there is no need to posit a personal God, distinct from the universe, as an explanation for the observed complexity.
Events of emergence are the
"quanta" of evolution. They lead to the creation of new systems with
new identities, obeying different laws and possessing different
properties. In such systems, the behaviour of the whole depends on the behaviour of the parts (a "reductionistic" view), but the behaviour of
the parts is at the same time constrained or directed by the behaviour
of the whole (a "holistic" view). (see downward causation)
A fundamental type of emergence is the "meta-system transition" , which results in a higher level of control while increasing the overall freedom and adaptivity of the system. Examples of
metasystem transitions are the emergence of multicellular organisms, the emergence of the capacity of organisms to learn, and the emergence of human intelligence.
See further: Turchin's paper on Cybernetic Metaphysics.
In a traditional systems philosophy "organization" might be seen as the fundamental principle of being, rather than God, matter, or the laws of nature. However it still begs the question where this organization comes from. In our evolutionary-systemic philosophy, on the other hand, the essence is the process through which this organization is created.
Therefore, our ontology starts from elementary actions, rather than from static objects, particles, energy or ideas. These actions are the primitive elements, the building blocks of our vision of reality, and therefore remain undefined. Actions are in not general not deterministic but involve an element of freedom. A sequence of actions constitutes a process. Our ontology is thus related to the process metaphysics of Whitehead and Teilhard de Chardin. Its historical origin can be traced back even further to the development from Kant to Schopenhauer.
Relatively stable "systems" are
constructed by such processes through the mechanism of variation and selection. This leads to the spontaneous emergence of more complex
organizations during evolution: from space-time and elementary
particles, to atoms, molecules, crystals, DNA, cells, plants, animals,
humans, and human society and culture (see the history of evolution). This developmental sequence provides us with a basis for our cosmology. Because of this self-organization of the universe, there is no need to posit a personal God, distinct from the universe, as an explanation for the observed complexity.
Events of emergence are the
"quanta" of evolution. They lead to the creation of new systems with
new identities, obeying different laws and possessing different
properties. In such systems, the behaviour of the whole depends on the behaviour of the parts (a "reductionistic" view), but the behaviour of
the parts is at the same time constrained or directed by the behaviour
of the whole (a "holistic" view). (see downward causation)
A fundamental type of emergence is the "meta-system transition" , which results in a higher level of control while increasing the overall freedom and adaptivity of the system. Examples of
metasystem transitions are the emergence of multicellular organisms, the emergence of the capacity of organisms to learn, and the emergence of human intelligence.
See further: Turchin's paper on Cybernetic Metaphysics.
`Meta' in Greek means over, and -- since when you jump over
something you find yourself behind it in space and after in time
-- it is also understood as behind and after. The word `metaphysics'
is said to originate from the mere fact that the
corresponding part of Aristotle's work was positioned right after the part
called `physics'. But it is not unlikely that the term won a
ready acceptance as denoting the whole field of knowledge because
it conveyed the purpose of metaphysics, which is to reach beyond
the nature (`physics') as we perceive it, and to discover the
`true nature' of things, their ultimate essence and the reason
for being. This is somewhat, but not much, different from the way
we understand `meta' in the 20-th century. A metatheory is a
theory about another theory, which considered as an object of
knowledge: how true it is, how it comes into being, how it is
used, how it can be improved, etc. A metaphysician, in contrast,
would understand his knowledge as a knowledge about the world,
like that of a physicist (scientist, generally), and not as a
knowledge about the scientific theories (which is the realm of
epistemology).
If so, metaphysics should take as honorable a place in
physics as metamathematics in mathematics. But this is very far
from being the case. It would be more accurate to describe the
situation as exactly opposite. Popularly (and primarily by the
`working masses' of physicists), metaphysics is considered as
something opposite to physics, and utterly useless for it (if not
for any reasonable purpose). I will argue below that this
attitude is a hangover from the long outdated forms of empiricism and positivism. I will argue that metaphysics is physics.
A detractor of metaphysics would say that its propositions
are mostly unverifiable, if intelligible at all, so it is hardly
possible to assign any meaning to them. Thales taught that
everything is water. The Pythagoreans taught that everything is
number. Hegel taught that everything is a manifestation of the
Absolute Spirit. And for Schopenhauer the world is will and
representation. All this has nothing to do with science.
But Democritus, and then Epicurus and Lucretius taught that
the world is an empty space with atoms moving around in it. In
due time this concept gave birth to classical mechanics and
physics, which is, unquestionably, science. At the time of its
origin, however, it was as pure a metaphysics as it could be. The
existence of atoms was no more verifiable than that of the
Absolute Spirit. Physics started as metaphysics. This is far
from an isolated case.
The question of verifiability is a part of our understanding
of the nature of language and truth. What is the meaning of words
and other objects of a language? The naive answer is: those
things which the words denote. This is known as the reflection
theory of language. Language, like a mirror, creates certain
images, reflections of the things around us. With the reflection
theory of language we come to what is known as the correspondence
theory of truth: a proposition is true if the relations between
the images of things correspond to the relations between the
things themselves. Falsity is a wrong, distorted reflection. In
particular, to create images which correspond to no real thing in
the world is to be in error.
With this concept of meaning and truth, any expression of
our language which cannot be immediately interpreted in terms of
observable facts, is meaningless and misleading. This viewpoint
in its extreme form, according to which all unobservables must be
banned from science, was developed by the early nineteenth-century
positivism (August Comte). Such a view, however, is
unacceptable for science. Even force in Newton's mechanics
becomes suspect in this philosophy, because we can neither see nor
touch it; we only conclude that it exists by observing the
movements of material bodies. Electromagnetic field has still less of
reality. And the situation with the wave function in quantum
mechanics is simply disastrous.
The history of the Western philosophy is, to a considerable
extent, the history of a struggle against the
reflection-correspondence theory.
We now consider language as a material to create
models of reality. Language is a system which works as a whole,
and should be evaluated as a whole. The job the language does is
organization of our experience, which includes, in particular,
some verifiable predictions about future events an the results of
our actions. For a language to be good at this job, it is not
necessary that every specific part of it should be put in a direct
and simple correspondence with the observable reality.
A proposition is true if, in the framework of the language
to which it belongs, it does not lead to false predictions, but
enhances our ability to produce true predictions. We usually
distinguish between factual statements and theories. If the
path from a proposition to verifiable predictions is short and
uncontroversial, we call it a factual statement. A theory is
but only through some intermediate steps, such as reasoning,
computation, the use of other statements. Thus the path from a
theory to predictions may not be unique and often becomes
debatable. Between the extreme cases of statements that are
clearly facts and those which are clearly theories there is a
whole spectrum of intermediate cases.
The statement of the truth of a theory has essentially the
same meaning as that of a simple factual statement: we assert
that the predictions it produces will be true. There is no
difference of principle: both factual statements and theories are
varieties of models of reality which we use to produce
predictions. A fact may turn out to be an illusion, or
hallucination, or a fraud, or a misconception. On the other
hand, a well-established theory can be taken for a fact. And we
should accept critically both facts and theories, and re-examine
them whenever necessary. The differences between facts and
theories are only quantitative: the length of the path from the
statement to verifiable predictions.
This approach has a double effect on the concept of existence.
On the one hand, theoretical concepts, such as mechanical
forces, electromagnetic and other fields, and wave functions,
acquire the same existential status as the material things we see
around us. On the other hand, quite simple and trustworthy
concepts like a heavy mass moving along a trajectory, and even the
material things themselves, the egg we eat at breakfast, become
as unstable and hazy as theoretical concepts. For to-day's good
theory is to-morrow's bad theory. We make and re-make our
theories all the time. Should we do the same with the concept of an
egg?
Certainly not at a breakfast. But in theoretical physics an
egg is something different from what we can eat: a system of
elementary particles. This makes no contradiction. Our language
is a multilevel system. On the lower levels, which are close to
our sensual perception, our notions are almost in one-to-one
correspondence with some conspicuous elements of perception. In
our theories we construct higher levels of language. The concepts
of the higher levels do not replace those of the lower levels, as
they should if the elements of the language reflected things "as
they really are", but constitute a new linguistic reality, a
superstructure over the lower levels. We cannot throw away the
concepts of the lower levels even if we wished to, because then
we would have no means to link theories to observable facts.
Predictions produced by the higher levels are formulated in terms
of the lower levels. It is a hierarchical system, where the top
cannot exist without the bottom.
Recall the table describing four types of langage-dependent
activities in our discussion of formalization. Philosophy is characterized by abstract
informal thinking.
The combination of high-level abstract constructs used in
philosophy with a low degree of formalization requires great
effort by the intuition and makes philosophical language the most
difficult type of the four. Philosophy borders with art when it
uses artistic images to stimulate the intuition. It borders with
theoretical science when it develops conceptual frameworks to be
used in construction of formal scientific theories.
Top-level theories of science are not deduced from
observable facts; they are constructed by a creative act, and their
usefulness can be demonstrated only afterwards. Einstein wrote:
"Physics is a developing logical system of thinking whose
foundations cannot be obtained by extraction from past experience
according to some inductive methods, but come only by free fantasy".
This "free fantasy" is the metaphysician's. When Thales said
that all is water, he did not mean that quite literally; he surely was
not that stupid. His `water' should rather be translated as `fluid',
some abstract substance which can change its form and is infinitely
divisible. The exact meaning of his teaching is then: it is
possible to create a reasonable model of the world where such a
fluid is the building material. Is not the theory of
electromagnetism a refinement of this idea? As for the Pythagoreans,
the translation of the statement 'everything is number' is that
it is possible to have a numerical model of the Universe and everything
in it. Is not the modern physics such a model?
When we understand language as a hierarchical model of
reality, i.e. a device which produces predictions, and not as a
true picture of the world, the claim made by metaphysics is read
differently. To say that the real nature of the world is such and
such means to propose the construction of a model of the world
along such and such lines. Metaphysics creates a linguistic
structure -- call it a logical structure, or a conceptual
framework -- to serve as a basis for further refinements. Metaphysics
is the beginning of physics; it provides fetuses for future
theories. Even though a mature physical theory fastidiously
distinguishes itself from metaphysics by formalizing its basic
notions and introducing verifiable criteria, metaphysics in a very
important sense is physics.
The meaning of metaphysics is in its potential. I can say
that Hegel's Absolute Spirit is meaningless for me, because at
the moment I do not see any way how an exact theory can be
constructed on this basis. But I cannot say that it is
meaningless, period. To say that, I would have to prove that
nobody will ever be able to translate this concept into a valid
scientific theory, and I, obviously, cannot do that.
It takes usually quite a time to translate metaphysics into
an exact theory with verifiable predictions. Before this is done,
metaphysics is, like any fetus, highly vulnerable. The task of
the metaphysician is hard indeed: he creates his theory in
advance of its confirmation. He works in the dark. He has to
guess, to select, without having a criterion for selection.
Successes on this path are veritable feats of human creativity.
Kant synthesized empiricism and rationalism by seeing
knowledge as organization of sensations by our mind. Space, time, and
other categories are not given us in sensations. They are our
forms of perception, the way we organize sensations. This is how
the synthetic judgments a priory become possible. They speak
about the methods of our mind which are inborn and do not depend
on sensations.
From the cybernetic point of view, sensations are at the
input of our cognitive apparatus, the nervous system. This input
is then processed by a huge hierarchical system. As the signals
move up in the hierarchy, sensations become perceptions, and then
conceptions (there are no sharp boundaries, of course). How much
is coming from the reality, the sensations, and how much from the
way we process them?
Kant considered the categories as a sort of final, ultimate,
because they are rooted in the way our brains are made. The
only possible geometry for him was Euclidean geometry.
And here comes the non-euclidean geometry of Lobachevsky.
This could be a disaster if we did not interpret Kant's ideas from
a modern point of view.
We see no contradiction
between the use of inborn ways of analysis of sensation and
the refusal to take these ways as the only possible and
universally applicable. We cannot change
our brain (for the time being, at least),
but we can construct world models which are counter-intuitive to
us.
We have two cybernetic systems which make world models: our
brain, with its neuronal models, and our language, in which we
create symbolic models of the world. The latter are certainly
based on the former. But the question remains open: at what level
of the neuronal hierarchy do the symbolic models take up?
Compare mathematics and classical mechanics. Mathematics
deals with objects called symbolic expressions (like numbers, for
example). They are simple linear structures. We use our nervous
system to identify some symbols as "the same". For example, this
symbol: A is the same as this: A. Another thing we want is to
know that if you add a symbol B to A, and to another A you add
another B, then the results, i.e. AB, will be identical again.
The totality of such elementary facts could hardly be codified,
exactly because of their basic nature. They are not eliminable.
Even if we pick up a number of axioms about symbolic expressions,
as we do, e.g., in the theory of semi-groups, we shall still use
rules of inference to prove new facts about them, and since the
rules and the formal proofs are again symbolic expressions, we
shall rely again on the basic facts about symbolic expressions in
the original informal way.
In classical mechanics we use much more of our neuronal
world models. There is a three-dimensional space; there is time;
there are the concepts of continuity, a material body, of cause
and effect, and more.
Mach and Einstein would be, probably, impossible without
Kant. They used the Kantian principle of separating elementary
facts of sensations and organizing these facts into a conceptual
scheme. But the physicists went further. Einstein moved from
the intuitive space-time picture given by the classical mechanics
down to the level of separate measurements, and reorganized
the measurements into a different space, the four-dimensional space-time
of the relativity theory. This space-time is now as
counterintuitive as it was in 1905, even though we have accustomed to it.
Hence what we call the paradoxes of the relativity theory. But
they do not bother us. We use a bit less of neuronal
models, and a bit more of symbolic models, that is all.
In quantum mechanics, the physicists went even further. They
rejected the idea of a material body located in the space-time
continuum. The space-time continuum is left as a mathematical
construct, and this construct serves the purposes of relating
micro and macro-phenomena, where it has the familiar classical
interpretation. But material bodies lost their tangible character.
The elementary objective facts are even lower in
the hierarchy than measurements; they are observations
which all occur in the world of macro-objects.
In the relativity theory observations
(measurements) at least belonged to the same universe as the
basic conceptual scheme: the space-time continuum. In quantum
mechanics, on the contrary, there is a gap between what we believe
to really exist, i.e. quantum particles and fields, and
what we take as the basic observable phenomena, which are all
expressed in macroscopical concepts: space, time and causality.
Of course, one can say that in the last analysis every theory
will explain and organize observable facts, and they always will
be macroscopic facts, because we are macroscopic creatures. Thus
a physical theory does not need the concept of ``real existence'';
even if it is a micro-world theory it operates on macro-world
observables. This is formally true. But the question is that of the
structure of a physical theory. We still want our theory to give
an answer to the question: what is REALLY existing? What is the
ultimate reality of physics? This question is not meaningless.
Its meaning is in the quest for a theory which would start with
concepts believed to correspond to that ultimate reality, and
then step by step construct observables from these
``really existing'' things. Somehow, it seems that such a theory
has better chances for success. If we have such a theory, and the real
existence is attributed to some things --- call them ex-why-zeds ---
and the theory is born out by experiment, then we can say that
the ex-why-zeds do really exist and that the world really consists
of ex-why-zeds. Ontologically, this will be as certain as
when we say that the apple is in a bowl on the basis of seeing it
and touching it.
The contemporary quantum mechanics does not meet this requirement.
It starts with space-time continuum, which in no sense
exists. Since Kant we know that it is only a form of our perception.
Suppose we are determined to construct a theory which is
built as required above. How should we go about the construction
of such a theory? We must go further down in the hierarchy of
neuronal concepts, and take them for a basis. Space and time must
not be put in the basis of the theory. They must be constructed
and explained in terms of really existing things.
This is where metaphysics should help us.
The goal of metaphysics is to
create world models which go down and down into the depth of our
experience. The concepts of the higher level of the neuronal
hierarchy are discounted as superficial; attempt is made to
identify the most essential, pervasive, primordial elements of
experience. But this is exactly the program we have just set for
ourselves. Kant's metaphysics had served as the philosophical
basis for the modern theories of physics. We see now that a
further movement down is required. Thus let turn to
the development of metaphysics after Kant.
Two lines of development became most visible: the German
idealism and Hegel in particular; and Schopenhauer.
The Hegelian line contributed to the development of
the theory of evolution, but in terms of ontology and epistemology
did not give
much. It is not analytical. It is a romantic picture of
a striving and struggling world. The basic entities and concepts are
obviously made up, as if created by an artist.
Schopenhauer, on the contrary is analytical. He does not
create a sophisticated picture of the world. He only gives an
answer to the question `what is the world': it is will
and representation.
Kant introduced the concept of the thing-in-itself for that
which will be left of a thing if we take away everything that we
can learn about it through our sensations. Thus the thing-in-
itself has only one property: to exist independently of the
cognizant subject. This concept is essentially negative; Kant did
not relate it to any kind or any part of human experience. This
was done by Schopenhauer. To the question `what is the thing-in-
itself?' he gave a clear and precise answer: it is will. The
more you think about this answer, the more it looks
like a revelation. My will is something I know from within.
It is part of my
experience. Yet it is absolutely inaccessible to anybody except
myself. Any external observer will know about myself whatever he
can know through his sense organs. Even if he can read my
thoughts and intentions -- literally, by deciphering brain signals --
he will
not perceive my will. He can conclude about the existence of my will
by analogy with his own. He can bend and crush my will through
my body, he can kill it by killing me, but he cannot in any way
perceive my will. And still my will exists. It is a thing-in-
itself.
What then is the world as we know it? Schopenhauer answers:
a 'Vorstellung'. This word was first translated into English as
an `idea', and then a `representation'. Both translations are not
very precise. In Russian there is a word for it which is a literal
translation of the German `Vorstellung': `predstavleniye'.
`Vorstellung' is something that is put in front of you.
It is a world picture we create ourselves -- and put in front of us,
so that to some extent it screens the real world. This aspect of
Vorstellung is not properly reflected either in 'idea'
or in 'representation'.
Let us examine the way in which we come to know anything
about the world. It starts with sensations. Sensations are not
things. They do not have reality as things. Their reality is that
of an event, an action. Sensation is an interaction between the
subject and the object, a physical phenomenon. Then the signals
resulting from that interaction start their long path through the
nervous system and the brain. The brain is tremendously complex
system, created for a very narrow goal: to survive, to sustain
the life of the individual creature, and to reproduce the species.
It is for this purpose and from this angle that the brain
processes information from sense organs and forms
its representation of the world.
Experiments with high energy elementary particles
were certainly not included into the goals for which the
brain was created by evolution. Thus it should be no surprise
that our space-time intuition is found to be a very poor
conceptual frame for elementary particles.
We must take from our experience only the most fundamental
aspects, in an expectation that all further organization of
sensations may be radically changed. These most elementary
aspects are: the will, the representation, and the action, which
links the two: action is a manifestation of the will
that changes representation.
Indeed, is it not the physical quantity of action that is
quantized and cannot be less than Plank's constant h, if it is
not zero? Why not see this as an indication that action should
have a higher existential status than space, time, matter? Of
course, it is not immediately clear whether the concept of action
as we understand it intuitively and the physical quantity that
has the dimension of energy by time and called 'action' are one and
the same, or related at all. That the physicists use the word `action' to
denote this quantity could be a misleading coincidence. Yet the
intuitive notion of an action as proportional to the energy spent
(understood intuitively) and the time passed does not seem
unreasonable. Furthermore, it is operators, i.e., actions
in the space of states, that represent observable (real!)
physical quantities in quantum mechanics, and not
the space-time states themselves!
Even if we reject these parallels and intuition as unsafe, it
still remains true that neither space, nor time, nor matter are
characterized by constant indestructible quanta, but
a combination of these: action. Is it not natural to take action
as a basis for the picture of the world --- if not for a
unifying physical theory?
But set aside physics. There is a branch of knowledge, cybernetics,
where action ontology comes naturaly because of its approach
to the description of the world. In cybernetics we abstract from
matter, energy, space, even time. What remains is interdependence
between actions of various kinds.
Communication, control, information -- all these are actions.
Taking action as an ontological
primitive we come to an intuitively acceptable and logically
consistent definition of its basic concepts.
Cybernetic ontology is ontology of action
In cybernetics we abstract from matter, energy, space, even time.
What remains is interdependence between actions of various kinds.
Communication, control, information -- all these are actions.
An action is a result of a free choice.
The state of the world defines (or rather is defined as) the
set of feasible actions for each will.
The act of will is to choose one of these.
We learn about action through our representations, i.e. our
knowledge about the external world.
When we ignore the agent, we speak of actions as events.
When we speak of actions
of human beings we know very well what the agent is: just the person
whose action it is. We reconstruct this notion, of course, starting
from our own "I". When we speak of animals, e.g. such as dogs,
we again have no doubt in the validity of the concept agent.
This reasoning can be continued to frogs, amoebas, and inanimate
objects. We say: "the bomb exploded and ship sank".
But what about a collision of two
elementary particles, of an act (sic!) of radioactive decay?
It is definitely an action, but whose action is it?
We do not know -- meaning that we have, at present, no picture,
model, or theory of the world which would make use of the agent of
this collision or emission. Thus we call this action an event.
Not that it has no agent:
by the nature of our concept, each action is performed by an agent.
We simply can say nothing about it, so we ignore it. It may well be that
in some future physical theory we shall speak about the agents of
subatomic events. It seems reasonable to speak of an agent which
comes into being for the express purpose of causing an act of
radioactive decay. At each moment in time this agent makes a choice
bewteen decay and not decay. This immediately explains the exponential
law of radioactivity.
When we speak of an action, we speak also of an agent that performs
the action. An agent is the carrier of will, the entity that chooses
between possible actions. We do not see agents, we see only what they
are doing. But we use the concept of agent to create models of the world.
We break what is going on in the world into parts and call these parts
actions. Then we notice that actions have certain structure. Some actions
are taking place in parallel, others consecutively. A number of actions
can be considered as one complex action (cf. process). We start the description
of this structure by introducing the notion of agents that perform actions.
The same agent may perform, consecutively, some number of actions.
Different agents may execute actions in parallel. The agent of a complex
action can, somehow, call a "subcontractor" agent.
Introduction of agents is, speaking informally, our first theory
of the world. Further development of the theory can go in various
directions. Since the thinking being understands agent seeing himself
as the primary model, it is natural that in primitive societies the concept
of agent is understood anthropomorphically: as something which is very
similar, if not identical, to ourselves. Hence the animism of primitive
thinking: understanding of all actions as initiated by various kinds
of spirits or other imaginary creatures.
The development of modern science banned spirits from the picture of the
world. But agents, cleared from anthropomorphism, still remain,
even though the physicists do not call them so. What is Newtonian force
if not an agent that changes, every moment, the momentum of a body?
Physics concentrates on the description of the world in space and
time; it leaves -- at least at the present day -- the concept of angent
implicit. We need it explicitly because of our metaphysics based
on the concept of action, not to mention the simple fact that cybernetics
describes, among other things, the behavior of human agents.
(This last field of application of cybernetics is, of course, one of the
reasons for our metaphysics).
Event is an action abstracted from the agent.
Agents come into, and go out of, existence. For centuries philosophers
grappled with a problem: how to distinguish simple ("quantitative") changes
from the cases where something really "new" emerges. What does it mean
to be "new", to emerge? In our theory this intuitive notion is formalized
as the coming of a new agent into existence. An action can lead to
an emergence of new agents.
Take, once again, radioactive decay. A neutron
suddenly chooses to break down into a proton, electron and neutrino.
We saw one agent: the neutron. Now it disappeared, but we see three new
agents which will meet their fate independently. This is an emergence.
In the case of complex actions, such as the birth of a baby, we can
argue about the exact time of the event, because we have more than one
reference system in which to describe actions. As a member of society,
the baby emerges at birth. As an object of embryology it emerges
at the moment of egg fertilization.
A set of actions is referred to as a domain. Theories (models
of the world) we construct are never universal. They are always applicable
to some part of the reality only. This part is the domain of the theory.
When we apply a theory, we assume that only those actions take place
which are within the domain. Make an action which is not included
in the domain, and the whole theory may become out of place.
The states of the world are defined as subsets of the domain of the theory.
Other actions are ignored; they may be either irrelevant, when they
have no impact on the legitimacy of the theory, or prohibited, when
they make the theory unapplicable.
A distinction can be seen as an element of cognitive structuration. Indeed, any process of perception implies a classification between phenomena. This classification operation has two aspects :
Spencer-Brown (1969) has proposed general axioms for distinctions. With these axioms, he has shown that a set of distinctions has a Boolean algebra structure, isomorphic to the algebra of classes in set theory or to the algebra of propositions in logic (Spencer-Brown, 1969). Spencer Brown showed that distinction algebra implies propositional calculus. B. Banaschewski (1977) showed the opposite entailment in
See further:
In many minds, science is still associated with the deterministic
picture of the world, as it was in the nineteenth century.
The modern science, however, draws a picture which is quite different.
The world of the nineteenth century was, broadly, as follows.
Very small particles of matter
move about in virtually empty three-dimensional space. These
particles act on one another with forces which are uniquely
determined by their positioning and velocities.The forces of
interaction, in their turn, uniquely determine, in accordance
with Newton's laws, the subsequent movement of particles. Thus
each subsequent state of the world is determined, in a unique
way, by its preceding state.Determinism was an intrinsic feature
of the scientific worldview of that time. In such a world there
was no room for freedom: it was illusory. Humans, themselves
merely aggregates of particles, had as much freedom as wound-up
watch mechanisms.
In the twentieth century the scientific worldview has undergone a radical change.
It has turned out that subatomic physics cannot be understood
within the framework of the Naive Realism of the nineteenth
century scientists. The theory of Relativity and, especially,
Quantum Mechanics require that our worldview be based on Criti
cal Philosophy, according to which all our theories and mental
pictures of the world are only devices to organize and foresee
our experience, and not the images of the world as it "really"
is. Thus along with the twentieth-century's specific discove
ries in the physics of the microworld, we must regard the inevi
tability of critical philosophy as a scientific discovery -- one
of the greatest of the twentieth century.
We now know that the notion that the world is "really" space
in which small particles move along definite trajectories, is
illusory: it is contradicted by experimental facts. We also know
that determinism, i.e. the notion that in the last analysis all
the events in the world must have specific causes, is illusory
too. On the contrary, freedom, which was banned from the science
of the nineteenth century as an illusion, became a part, if not
the essence, of reality. The mechanistic worldview saw the laws
of nature as something that uniquely prescribes how events should
develop, with indeterminacy resulting only from our lack of
knowledge; contemporary science regards the laws of nature as
only restrictions imposed on a basically non-deterministic world.
It is not an accident that the most general laws of nature are
conservation laws, which do not prescribe how things must br,
but only put certain restrictions on them.
There is genuine freedom in the world. When we observe it
from the outside, it takes the form of quantum-mechanical
unpredictability; when we observe it from within, we call it our
free will. We know that the reason why our behaviour is unpredictable
from the outside is that we have ultimate freedom of
choice. This freedom is the very essence of our personalities,
the treasure of our lives. It is given us as the first element of
the world we come into.
Logically, the concept of free will is
primary, impossible to derive or to explain from anything else.
The concept of necessity, including the concept of a natural law,
is a derivative: we call necessary, or predetermined, those
things which cannot be changed at will.
The attributes of a god or God vary from one religion to another.
In polytheistic religion (poly = many, theos = god) several of
these beings are posited. They are usually presumed to be immortal,
and to control aspects of nature or human destiny. Although
invisible, they are imagined to be human-like or animal-like in
appearance.
In monotheistic religions (monos = one) God is usually viewed as
an all- powerful and omnipresent being who created and still sustains
the universe. He is thought to be incorporeal, but possessed of a
human-like mind capable of planning actions, and of powers capable of
carrying out those actions in the real world.
In Judaism, Christianity and Islam, God also has a human-like
personal aspect, as the perfectly good, perfectly just, all-knowing
judge of human actions and thoughts. He allegedly cares for and loves
each one of us personally, and is merciful and forgiving if we accept
him.
In the metaphysics of Principia Cybernetica, there is no need to posit the existence of a personal God, as an all-powerful, intelligent agent which governs the universe but which is external to it. Indeed, the role of God as creator and director of the universe is taken over by self-organizing evolution. On the other hand, if such an agent with the traditional attributes of omnipotence, omniscience and perfect goodness would be posited, this would lead to logical inconsistencies. There are many arguments supporting this conclusion.
However, this still leaves open a few philosophical positions. Which position you prefer is more a matter of taste than a matter of logic, since they seem equivalent in most practical respects. The simplest one is atheism, which assumes that there is no God, and thus no need to think about the concept. A more subtle approach is pantheism, where the word God is redefined and is equated with the
universe and nature.
In this spirit of pantheism, God might be seen as the highest level of control
in the Universe. God is for the Universe what human will is for the human body.
Natural laws are one of the manifestations of God's will. Another manifestation is the evolution of the Universe: the Evolution. Finally, there is the "intermediate" position of agnosticism, which simply assumes that we don't know whether God exists, since none of the existing arguments can prove that God either exists or does not exist.
The major philosophical criticisms of God as viewed by Judaism,
Christianity and Islam are as follows:
None of these criticisms apply to the God of pantheism, which is
identical with the universe and nature.
Pantheism is distinguished
from panentheism, which holds that God is in everything, but also transcends
the Universe.
Strict pantheism is not a theism. It does not believe in a transcendent
or personal God who is the creator of the universe and the judge of humans.
Many pantheists feel the word "God" is too loaded with these connotations and
never use the word in their own practice - though they may use it to simplify,
or to explain things to theists.
Pantheism has often been accused of atheism, and not just because it
rejects the idea of a personal creator God. Strict
Because it shares these naturalistic beliefs with atheism, the arguments
for pantheism are the same as the arguments for atheism. Pantheism puts
forward exactly the same critiques of transcendental religions and
supernatural beliefs as does atheism. It is a secular religion, firmly rooted
in the real world of the senses and of science.
This form of pantheism is identical with movements variously called
religious atheism, affirmative atheism, Monism, or Cosmism. It is also very
close to Taoism, some forms of Chinese and Japanese Buddhism, and neo-
Confucianism.
Strict pantheism differs from conventional atheism only in its emotional
and ethical response to the material universe. It focusses not simply on
criticizing transcendental beliefs and religions, but stresses the positive
aspects of life and nature - the profound aesthetic and emotional responses
that most people feel towards nature and the night sky.
Naturalistic pantheism draws ethical conclusions from these feelings.
Humans should seek a closer harmony with nature. We should preserve
biodiversity and the delicate ecological balances of the planet, not just as a
matter of survival, but as a matter of personal fulfilment.
Pantheism offers ways of expressing these feelings in ceremonies,
celebrating significant times and places which underline our links with
nature, the solar system and the universe. All this is possible without
retreating one millimeter from the rigorously empirical attitude to reality
found in modern science.
There are other forms of pantheism.
An alternative, quite common among New Agers, is pan-psychic pantheism -
the belief that the universe/God has a collective soul, mind or will. This
version was most clearly expressed by
For further background, see:
The simplest argument for atheism follows from Occam's Razor: from different equivalent explanations, choose the simplest one. If we cannot explain more things by postulating the existence of God than we can without, then we should prefer the theory without. The fact that this principle is not sufficient to prove that God does not exist, is not very relevant. After all, nobody can prove that unicorns, flying toasters or 23-legged purple elephants do not exist, but that does not make their existence any more likely. (see also:
This assumes that the existence of God does not explain anything. However, the most typical argument for the existence of God is that creation by God is needed to explain the complexity of the universe around us. Apart from the fact that that same complexity can already be explained by straightforward principles of evolution and self-organization, the introduction of God does not in any way contribute to explanation, since it just pushes the phenomenon to be explained one step away. If God explains the existence of the universe, then what explains the existence of God? Since the concept of God is neither simpler nor more intuitive than the concept of the Universe, explaining God's origin is not in any way easier than explaining the origin of the Universe. On the contrary, since God is in principle unknowable, we cannot even hope to explain His coming into being. On the other hand, although the Universe may never be grasped in its totality, there are definitely many aspects of it that are observable and understandable, and lend themselves to ever more complete explanations. In conclusion, postulating God as an explanation does not only make the theory unnecessarily complicated, it even obscures those phenomena that might have been explained otherwise.
One must note that atheism is not in contradiction with religion. In its original, Latin sense, religion means "that which holds together", implying a kind of overarching philosophy and system of ethics that guides society as a whole, without necessary reference to God. Also in the more practical sense, several "religions", including Zen Buddhism, Taoism and Confucianism, lack any idea of God, and thus may be properly called "atheist religions". Also the different emotions that typically accompany religous experiences, such as the feeling of being part of a larger whole, can very well be experienced by a atheists, leading to what may be called "atheist religiosity".
See also: the
Cybernetics starts where metaphysics ends. It takes for granted the
notions of system, process, state and control as the primary elements
of models to construct. This is its difference from physics, which
takes space, time and matter as the primary concepts. It does not follow
that cybernetics may do completely without physical notions and
vice cersa: the question is that of the main focus. Boundaries between
various provinces of knowledge are blurred by constant lebding and borrowing.
When we look at the modeling scheme, we see four nodes representing
'states of affairs', or 'states of the world'. What are those states?
To answer this question let us ask ourselves: if action is the primary
reality, how do we distinguish between various states of the world?
The answer can be: by being able to do various different actions.
For example, if the state of affairs is such that there is an apple
on the table in front of me, a can reach it and pick it up. If there is
no apple this is impossible. If the moon is on the night sky, I can
execute the action of observing it. For this purpose I rotate my head in a
certain way and keep my eyes open. Observation is a kind of action.
Thus we could define a state of the world as a set of actions that I
(the subject of knowledge) can take.
But there are states of another type,
which do not fit this definition. If I feel pain, or am frustrated, or
elated, angry, or complacent, this has no effect on the actions I can
take. It affects only the choices I am going to make selecting from the
same set of possible actions. Indeed, if my hand is over a gas heater
and hurts (say, gently, for plausibility), I still have the choice between
keeping the hand where it is, or withdrawing. But, obviously, the more it hurts, the more likley I am to withraw it.
Thus we come to distinguish between:
(a) a physical state, which is a set of possible actions for the
subject 'physical' actions; and
(b) a mental state, which influences the choices to be made by the subject,
but does not alter the set of possible choices.
When speaking of "states" without any of the two adjectives, we shall
mean physical states.
The distinction between (a) and (b) reflects the fundamental distinction
between "I" and "not-I".
Why should we consider action as more basic and primary than state?
After all, we register an action when the states of the world changes.
The reason is this: a state can be understood and characterized
in terms of actions -- we have just defined it as a set of possible actions.
An action, however cannot be defined through states. When we define
an action as a change of the state, we introduce something new, which is
not present in the idea of a state; change is, essentially, an action
abstracted from the actor that executes it.
The following observation confirms the primacy of action
over state. When we start thinking about constructing a model of the world
on the basis of these concepts, we tend to believe that we will need
a relatively few types of actions, while the set of possible states of the
world is expected to be much greater and much more complex.
In our mathematical model of semantics we shall denote the set of all
possible action by A. We do not yet know what this set is, or rather
what it should be for our further models to be successful. It is possible
that various models of the world will start with various different sets A.
But with any A, the set of possible states of the world, which we shall
denote as W, is the powerset of A, W = P(A), i.e. the set of all subsets
of A. Thus an individual state w is an element of W. w \el W, and
a subset of A, w \subs A.
Among the most elementary actions known to us are small displacements
"in space". We have put the quotes, because people have accustomed to imagine
that some entity, called "space" exists as a primary reality, which
creates the possibility of moving from one point of this space to another.
Our analysis turns this notion topsy-turvy. Only actions constitute
observable reality; space is nothing but a product of our imagination
which we construct from small displacements, or shifts, of even smaller
objects called points. If x is such a shift,
then xx -- the action x repeated twice -- is a double shift, which we
would call in our conventional wisdom a shift at the double distance
in the same direction. On the other hand, we may want to represent a
shift x as the result of another shift x' repeated twice: x = x'x'.
It so happens that we can make three different
kinds of shifts, call them x, y, z, none of which can be reduced to
a combination of the other two. At the same time any shift w
can be reduced to a properly chosen combination of shifts x, y, z.
So we say that our space has three dimensions.
When we do nothing for a while we say that some "time" has passed.
In terms of actions, doing nothing is a special type of action.
If we denote it by t, then
tt is an action of waiting for two times longer than with t.
When we measure time, we take some repetative process, like one swing of
a pendulum, for a model of other processes. We may say, for instance, that
John needes 80 'pendulums' of time to smoke a cigarette. In terms of
the homomorphism picture, the state when John is lighting his cigarette
is w_1; the state when he extinguishes it is w_2; the language L is
the pendulum, with some kind of counter of swings; the mapping M is
registration of the current value of the counter. The process
M must be a real physical process, not just a mental association
of some states of the counter with some states of cigaret smoking -
the truth which has been dramatically demonstrated
by Einstein's relativity theory.
We often say that all real processes take place in space and time.
The meaning of such statements is that in addition to what really goes on,
we imagine some reference actions of consecutive shifts ("in space")
and waits ("in time") and esatblish relationships between these actions
and actual objects and processes. Thus, in accordance with Kant's view,
space and time are not observable realities, but our ways to organize
experience.
Henri Bergson was first to notice and emphasize the difference between
real time, in which we live and act,
and the objectified time of history and physics.
Imagine a pendulum which at each swing puts a mark on a
moving tape. We have a historical record of "the time moving". This
historic record is an object at every moment we look at it. We use it
as a part of our model of reality. We shall refer to the marks on the tape
as representing a model time. It is very much different from
the real time.
Real time is such that two moments of it never coexist. In model time
the moments coexists as different objects in some space. Thus Bergson
calls model time a projection of real time on space. Bergson's real time
is irrreversible. Model time, the time of Newton's mechanics, is reversable:
we read historical records equally well from left to right and from right
to left. The seemingly inconceivable feature of Feynman's diagrams, the
movement in the direction opposite to time, is explained simply by the fact
that the time of physical theories is model time, i.e. a spacial
phenomenon. Real time shows up in probability theory and statistical
physics. We are dealing there with real acts of choosing from a number
of possibilities. Hence this time is irreversible. In mechanics, to every
action there is an inverse action which brings back the original state.
So, when we project time on space the projection has an additional property
of reversibility. But the act of choosing has no inverse. If you drew
ticket No.13, you drew it. You can return it to the pool, but the fact
will still remain that it was No.13, and nothing else, that was drawn first
and then returned. You can choose, but you cannot "unchoose".
A model can be represented by an object in such a manner that the
potential user of the model would be able to create the original
model if he has the representation. In particular, any piece of knowledge
can be represented in this way. This is a case of objectification.
A a metasystem transition takes place:
a model, which is a process, "becomes" (not really -- it is only
represented by) an object; now we can manipulate these objectified
models, modify them and study them, thus creating models of
(objectified) models.
Some of these objectified models are not intended for a direct use,
that is to say, they must not be used for obtaining predictions.
They are used only as inputs to other models, so that those other models
could do ingenious predictions and serve as a basis for decision making.
We call such objectified models historic records. The manner in which
they are used can be usually described as updating. That is, the user
takes a historic record, modifies it according to some principles -
may be with the use of other models, and derives the model to be
actually used for the generation of predictions.
Semant.10. Objectification
We often want to think and speak about a process as something definit,
constant -- in other words, as an object. Then we objectify it, i.e.
replace the process, in reality or in our imagination, by an object.
Objectification is a kind of metasystem transition. Normally in a
metasystem transition we create a new process which controls the old one(s).
In objectification the new process controls not the old ones, but the
objects representing these processes.
The most usual form of objectification is definition. In mathematics,
for instance, we define algorithms as computational processes which
we expect to be executed in a certain fixed manner. The definition of an
algorithmic process is an object, usually a text in some formal language.
The semantics, i.e. the meaning, of the language is provided by a machine
which executes the process in accordance with its definition.
The famous Turing machine is an example.
The concept of a machine gives us a link between objects and associated
processes. A machine is a process which is controlled by its user
in a certain quite limited way: the user only sets up the machine,
i.e. puts into it certain objects (typically those would be the definition
of an algorithm and some initial data for it) and starts it. After that
the process goes on autonomously.
Let us analyze the meaning of statements of the form:
'C is the cause of the effect E', or simply 'C causes E'.
Here C is an action, and E a situation, i.e. a set of states of the
world deined by an abstraction function. Sometimes we speak of the
cause C as a situation too, but what we mean then is that this situation
leads inescapably to a certian action which causes E. Other times,
we speak of the effect E as an action, but this, again, for the same
reason that this action is an immediate result of the situation caused
by C. So, in the mainstream, the cuase is an action, and the effect
a situation.
The first attempt to explain the meaning of causality is to say
that whenever C takes place, E takes place also. But this is not
a satisfactory explanation. We see that after a day a night always comes,
but the day is not the cause of the night; it is rather the rotation
of the Earth. A simple observation of the sequence (C,E) is not
sufficient. C and E might be two effects of a common cause, or this
could be just a coincidence. That causal relation is something more than
sequence in time, was noted by many thinkers and is in agreement with
our intuition.
In search of the true meaning of causality consider the case when
the cause C is my own action. By my own we mean a reference to
the subject of knowledge. To give meaning to a statement, we must relate
it to generation of predictions; as a rule, we do this in the form of
modeling scheme (see model). The statement 'C causes E'
is translated as two predictions:
The first prediction:
Now suppose that C is not my action, but that of some other agent.
It may come as a surprize that this, seemingly innocuous, change radically
changes the picture. Now the action C must be a part of the initial
situation S. We shall represent this complex situation as S+obs(C), where
obs(C) stands for the fact that we observe some consequences of
the action C. We must remember that I can perceive an action directly
only when it is my own action; all other actions I perceive through my
sense organs as changes in the state of the world. I can use the concept
of action to construct modesl of reality; in particular, an action of a
fellow human I perceive by analogy with my own action, but this does not
alterate the basic fact that all agents except myself are given me only
through the manifestation of their actions. I am I, and all other agents
are they.
Thus we can try to express the meaning of causality in this case
as consisting of the following pair of predictions:
The first prediction:
Then is there any meaning in speaking about a cause which is not an action
of the subject of knowledge? We believe, there is, but it is a result
of a certain reduction of this case to the basic case where
the cause C is the subject's action. There is an additional element
introduced by the subject of knowledge in understanding causality
in the case of sombody's else action. It is a tacit assumption that
I could, somehow, allow or prevent the action of which I think
as a cause. The interpretation of the statement that
an action C of some agent causes E as the statement that if I,
the subject of knowledge, allow C to take place, then E ensues;
however, if I somehow prevent it, there will be no E.
This case of causality is the following modesl of the world:
The first prediction:
True False
---------------
^ ^
| |
S | | E
| |
| prevent C |
----------------
What I really imagine when I assume that I stop the rotation of the Earth
is a relatively small (of the size convenient for imagination) rotating
sphere, which I then cause tho stop rotation. This is a part of my model
of the Earth and the Sun which explains the alternation of day and night.
There are to models here. First I construct the Sun-Earth model,
then I see that "days" and "nights" in that model are caused by the rotation
of "the Earth", and then I make a jump back to real days amd nights
and say that this is caused by the rotation of the Earth.
As required by our epistemology, we explained causal statements
as certain models of the world. We might now ask: what about the
concept of model itself? Does it not include the idea of cousality?
The answer is yes, it does. Moreover it is based on causality.
The ability to make predictions and the existence of causality in the world
is, essentially, the same.
Of the four lines in the modeling scheme, one represents a free action
of the subject of knowledge, the other three are functions, which are
devices relying on causality: give me an inpout, and I will give output.
To define formally what those functions are, we could describe them
as causal relations, i.e. explain in terms of new models, metamodels.
Then we could construct models of metamodels, etc. This we leave nowhere
and add nothing to understanding. The concept of modeling is so fundamental
that its meaning cannot be reduced to anyhting less than itself.
Thus we take it for the basis.
We saw that the actions of the subject of knowledge make a necessary
element in understanding causality. The relation of causality is not
directly observable.
We create models of the world using one or another machine
to implement the causal, functional, relation. Then we apply our models
to the world and see whether they work properly as predictors. Thus
causality, as Kant first indicated, is not among our immediate sensual data,
but is, rather, our basic way to organize those data.
See also: the Principle of Causality
An egg can be defined by pairs of actions which include:
Suppose I am aware of a tea-pot on the table in front of me.
This is a result of my having
the mechanism of abstraction in the brain. I recognize the image on my
retina as belonging to a certain set of images, the abstraction `tea-pot'.
But there is more to it. I perceive the tea-pot as an object.
The object `tea-pot' is certainly not a definite image on the retina
of my eyes; not even a definite part of it.
For when I turn my head, or walk around the table, this image changes all
the time, but I still perceive the tea-pot as the same object. The tea-pot
as an object must, rather, be associated with the transformation of the image
on my retina which results from the changing position of my eyes.
This is, of course, a purely visual concept.
We can add to it a transformation which produces my tactile sensations
given the position and movements of my fingers.
The general definition of an object suggested by this example consists
of three parts.
fa: R{ob \to R{ob
transforms a representation r \in R{ob into fa(r) = r'
which is expected as a result of action a.
b = {fa: a \in Acogn}
It also can be seen as a subset of
Acogn x Robx Rob.
The set Acogn is the domain of the index a; the set Rob
is the domain and co-domain of the functions of the family.
When I perceive an object b, I have a representation r
which belongs to the set Rob; I then execute some cognitive actions,
and for each such action a I run my mental model, i.e. perform
the transformation fa on r. If this anticipated representation
fa(r) matches the actual representation r' after the action a:
fa(r) = r'
then my perception of the object b is confirmed;
otherwise I may not be sure about what is going on. Observing
a tea-pot I check my actual experience against what
I anticipate as the result of the movements of my head and eyeballs.
If the two match, I perceive the tea-pot
as an object. If I travel in a desert and see on the horizon castles and
minarets which disappear or turn topsy-turvy as I get closer,
I say that this is a mirage, an illusion, and not a real object.
The concept of an object is naturally (one is tempted to say, inevitably)
arises in the process of evolution. It is simply the first stage in
the construction of the world's models. Indeed,
since the sense organs of cybernetic animals
are constantly moving in the environment, these actions are the first
to be modeled. In the huge flow of sensations a line must be drawn between
what is the result of the animal's own movements, and other changes
which do not depend on the movements, are objective.
Description of the world in terms of objects factors out
certain cognitive actions.
Function fa factors out the action a by predicting
what should be observed when the only change in the world is
the subject's taking of the action a. If the prediction comes true,
we interpret this as the same kind of stability as when nothing changes
at all. The concept of object btings in a certain invariance, or stability,
in the perception of a cybernetic system that actively explores
its environment.
Very often processes have the following additional feature:
Also, there are processes which have a definite initial stage,
but may or may not have a final stage, i.e. a process may be infinite.
Processes often are contrasted with objects. The most important
feature of objects is -- by definition -- their constancy with respect to
certain cognitive actions. The concept of a process, on the contrary,
represent an ongoing change.
The most usual way of speaking of objects and processes is a criss-cross
between the two concepts: a process, the stages
of which are objects not identical to each other. On a smaller time scale
we observe constancy with respect to some cognitive actions, which gives
us the reason to speek of it as an object. On a larger time scale,
this is a process, and we say that the object is changing.
One can see from this definition that process is a very general concept.
An object may be seen as a special kind of process where there is no change.
Everything is a process, if we look at it in a certain way.
See also: process metaphysics
The number is a conceptual scheme, an abstraction of the second
level from specific numbers: 1, 2, 3, ... etc. The abstraction
procedure to recognize specific numbers is counting.
Counting is based on the ability to divide the surrounding world
up into distinct objects. This ability emerged quite far back in the course
of evolution; the vertebrates appear to have it in the same degree as
humans do. The use of specific numbers is a natural
integrated description complementary to the differential
description by recognizing distinct objects. This ability would certainly
be advantageous for higher animals in the struggle for existence.
And cybernetic apparatus for counting could be very simple --
incomparably simpler than for recognition
of separate objects in pictures.
Yet nature, for some reason, did not
give our brain this ability. The numbers we can directly recognize
are ridiculously small, up to five or six at best (though it can be
somewhat extended by training). Thus the number 2 is a neuronal
concept, but 20 and 200 are not. We can use them only through counting,
creating artificial representqations in the material external to the brain.
The material may be, and was historically, fingers and toes, then
pebbles, notches etc., and finally sophisticated signes on paper and
electronic states of computer circuitry. For theoretical purposes the best
is still the ancient-style representation where a chosen symbol, say '1'
stands for one object. Thus 2 is '11', and 5 is '11111'.
In mathematics and philosopy we find two concepts of infinity:
potential infinity, which is the infinity of a process which never
stops, and actual infinity which is supposed to be static and
completed, so that it can be thought of as an object.
The cybernetic philosopy readily embraces the concept of potential
infinity; in fact, it is hard to see how we can avoid it.
We say that a process ends when it reaches a certain stage. In a
particular case, we can define the end stage so that it never takes place.
As every general notion, this is an abstraction: we have abstracted from
the practical impossibilty to run any real process infinitely, and in fact,
for very long. In this abstraction, no matter how long we have run
the process, we always can do, or observe, the next step. This is why this
infinity is called potential. At every specific stage the process involves
no more than quite a finite reality; it is infinite only potentially.
For actual infinity we have no place in our system of concepts.
On the intuitive level, we cannot imagine anything that would qualify
as actual infinity, because neither we, nor our evolutionary predecessors
never had anything like that in experience. When we try to imagine
something infinite, e.g., infinite space, we actually imagine a process
of moving form point to point without any end in sight. This is
potential, not actual, infinity.
On a more formal level we can demonstrate the incompatibility of
the concept of actual infinity with our cybernetic understanding of
meaning. Indeed, suppose that some abstraction r represent the concept
of an "infinite" object, and we use it while constructing a model.
According to our semantics, there must exist an abstraction
(representation) function F which recognizes whether a given state
of the world belongs to this concept, an if so, results in r.
Moreover, function F must, by definition, always require a finite time
for coming up with a definite result. If the "infinite" object can be
always recognized as such in a finite number of steps, it is not actually
infinite, because it can be adequately replaced by a finite object.
If, by the intuitive meaning of the "infinite" object r its recognition
may require infinite time, then abstraction function will have to work,
at least in some cases, infinitely, but then it is not a valid
abstraction function. Thus we cannot use the concept of actual infinity
at all.
As an example, consider the process of counting. We can imagine it going
on infinitely if we do not count real sheep or apples, but simply
produce concecutive numbers. Let us represent numbers (whole and positive)
by strings of the symbol '1'; then the process is:
1, 11, 111, 1111, ... etc. infinitely.
When we say that this process is infinite, we mean that whatever is the
current number, we can add one more '1' to it. Thus we deal with potential
infinity.
To convert it into an actual infinity, we must imagine an object that
includes in itself all whole numbers.
We call it the set of all positive whole numbers.
Suppose that such a thing exists. How would it be possible for an abstraction
function F to distinguish it from other objects, e.g. from the set
of all whole numbers with the exception of the number 10^{50}?
Intuitively, F must examine the infinite number of the elements of
the set. Since this is impossible to achieve in any finite time,
the needed function F does not exist.
What we can do, however, is to create an objectification of the
process which generates all whole numbers. A machine which initiates
this process (and, of course, never stops) is such an objectification.
This machine is a finite object. It can be made of metal, with an electric
motor as the agent causing the process of work. Or we can describe it
in some language addressing a human agent, but requirung only simple
"mechanical" actions uniquely defined at each stage of the process.
Such descriptions are known as {\algorithms}. If we use the English language
for writing algorithms, the machine, to be referred to as N,
could be as follows:
At the initial stage of the process produce the number '1'.
At each next stage take the number produced at the preceding stage
and produce the number obtained by adding '1' to it."
Now we can say that the set of whole numbers is N.
We have no objections against sets defined in this way. Their meaning
is crystal clear. Their infinity is still potential.
The problem with contemporary mathematics is that it operates with sets
that cannot be represented by finite mechanical generators.
They are uncountable.
The question of the nature and meaning of these sets is,
in the eyes of contemporqry mathemticians and philosophers, wide open.
Yet their usefulnes is abundantly demonstrated, and everybody believs
that their use will never lead to contradiction. Thus it is important for us
to interpret uncountable sets -- and the whole set theory -- in terms
of our cybernetic, constructive philosophy. If we were unable to do this,
it would undermine our claim that the basic principles on which
we build our philosophy are universally applicable and sufficient.
Fortunately, we can interpret set theory, as well as classical
and intuitionist logic, in our terms (see Foundations of logic and
mathematics). Our interpretation assigns quite definite meanings,
in our sense of the word, to the basic concepts of logic and set theory,
and does it without any recourse to the concept of actual infinity.
If there were no way
to interpret uncountable sets in our philosop
A domain is continuous if for every action a there exist
two actions a_1 and a_2 such that the result of the composite action
a_1 a_2 is the same as the result of a.
An action a is elementary if a \not= a_1 a_2 for any two
actions a_1 and a_2.
A domain is discrete if every action from it can be represented
by a finite sequence of elementary actions.
Observation is an abstraction of knowledge from the impact made by
mappings F(Wi) of the world's states Wi on the states Wi themselves.
For instance, when we watch a paly of billiards, the positions of
the balls are registered by means of the light thrown on the balls and
reflected into our eyes. We rightfully believe that the effect of the
lighting on the movements of the balls is negligible, so we speak about the
play in a complete abstraction from the way we know about it. This separation
is not always possible. Quantum mechanics deals with actions so elementary
that the means we use to know of them cannot be abstracted from.
Our ususal 'classic' notions of space and time include the abstraction
of observation. Indeed, the mental construction of a reference frame
uses shiftes and waits which are assumend to have no effect on the studied
processes; for quantum-mechanical processes this assumption is not valid,
and the classic space-time frame of reference looses its legitimacy,
becomes meaningless. One should not use in mental constructions and
experiments those things known not to exist.
We now arrive at the concept of the system, which we obviously do
not take to be fundamental. The definition of "system" is of course
one of the great philosophical issues of Cybernetics and Systems Science. A common definition is
"a group of units so combined as to form a whole and to operate in
unison" \cite{WEB89}. But there are dozens of definitions in the technical
literature, reflecting a wide range of philosophical perspectives:
Leaving aside issues of objectivity and subjectivity, realism and
antirealism, and formalism and constructivism, there are some common
characteristics which we can discover in all these definitions. System
requires at least the following:
Thus in the concept of the system we see the unification of many sets of
distinctions: the multiplicity of the elements and the singularity of the
whole system; the dependence of the stability of the whole on the activity
of the relation amongst the entities; the distinction between what is in
the system and what is not; and finally the distinction between the whole
system and everything else. In the activity of the relation which creates a
stable whole, we recognize a closure. Therefore, we define a system as that
distinction between the variety and stability of a closure on some multiple
other distinctions. We call the stability of the whole the persistence of the system: as long as the multiple distinctions
participate in the relation resulting in the stability of the whole system,
then the system exists, and persists.
In MST Theory, knowledge is understood as consisting of models that allow the
adaptation of a cybernetic system to its environment, by anticipation
of possible perturbations. Models function as recursive generators of
predictions about the world and the self. A model is necessarily simpler than the environment it represents, and this enables it to run faster than, i.e. anticipate, the processes in the environment. This allows the system to compensate perturbations before they have had the opportunity to damage the system.
Models are not static
reflections of the environment, but dynamic constructions achieved
through trial-and-error by the individual, the species and/or the
society. What models represent is not the structure of the environment but its action, insofar as it has an influence on the system. They are both subjective, in the sense of being constructed
by the subject for its own purposes, and objective, in the sense of
being naturally selected by the environment: models which do not
generate adequate predictions are likely to be later eliminated. Thus, the development of knowledge can best be understood as an evolutionary process characterized by variation mechanisms and selection criteria.
There
is no "absolutely true" model of reality: there are many different
models, any of which may be adequate for solving particular problems,
but no model is capable to solve all problems. The most efficient way
to choose or to construct a model which is adequate for the given
problem is by reasoning on a metacognitive level, where a class of
possible models can be analysed and compared. This requires a
metasystem transition with respect to the variety of individual
models.
In cybernetics we say that a purposive cybernetic system S has some
knowledge if the system S has a model of some part
of reality as it is perceived by the system. Informally, a model of
some process occurring in a system is a another system which somehow
mimicks, or simulates, that process;
thus by using the model it becomes possible to know
something about the modelled process without actually running it,
or predict developments before they actually happen.
The definition of the modeling scheme includes
an important assumption of non-interference:
that the procedure R (which is a sequence of actions), when it acts
on a state w of the world, does not change that state.
But we know from quantum mechanics that this assumption, strictly
speaking, never holds. When we deal with macroscopic phenomena we can,
nevertheless, use the non-interference assumpiton, because the impact of the instruments we use in R
on the state w can always be made insignificant.
But on the atomic and subatomic levels, we cannot abstract from the
action of the means we use to get information about the objects
studied.
There is one more non-interference assumption: the modeling procedure M_a
imitating the action a does not alter in any way the course of the action,
including the final result w_2.
Usually, this assumption is easily true; the most
salient case is that of an astronomer. His computations, certainly,
do not change the motion of celestial bodies. But when we try to apply
the modelling scheme to self-description, we may have problems.
So, a generalization of the modelling scheme is necessary, which would be
applicable even though the assumption of non-interference may not be true. Consider these two two-staged processes which we see in the
modeling scheme, and let them run in parallel
so that the mutual influence is not excluded:
The first process:
1. R(w_1) results in r_1;
2. M_a(r_1) results in r_2.
The second process:
1. a results in w_2;
2. R(w_2) results in r_2'.
The prediction produced by the model is that r_2 = r_2'.
We can go further, however, in the formalization of the concept
of prediction and making it more universal.
Wait for the time when both processes end and start the third
process C which compares r_2 and r_2'.
All three processes together constitute one
complex process, which is nothing else but the process of
testing the model. If our model is correct, then the process C,
and with it the whole complex process that tests the model, will
succeed, that is r_2 and r_2' will be found identical.
The model predicts that its test will succeed.
Therefore we introduce the formal concept of a prediction
However, even the definition of knowledge as a generator of predictions
is not general enough
to cover the whole concept. Pieces of our knowledge
(statements, or propositions) may not
necessarily produce verifiable predictions, but only some objects
that will be used to produce prediction. Moreover, they may produce objects
which produce objects which produce predictions, and so forth to any depth
of the hierarchy of knowledge objectifications.
A simple example from mathematics:
the equation x + y = y + x is not immediately verifiable, but it produces
-- this is a shortcut for 'we know how to use it to produce' -
such equations as 7 + 4 = 4 + 7. This object, in its turn, is still too
abstract for a direct verification. We can, however, verify the prediction
that four apples and seven apples can be added in either order with the
same result: eleven apples.
We come, therefore, to the following definition: a piece of knowledge is
an object which we can use to produce (generate) predictions or other
pieces of knowledge. This definition is recursive; it allows
a piece of knowledge which is not an immediate prediction,
or prediction generator, to produce other similar pieces (including itself)
any number of times, before some of its products
will produce predictions. The possibility is not excluded that
an object legitimately regarded as a piece of knowledge will
infinitely produce other pieces
without ever producing a single prediction: call this piece empty.
This is because with our very general definition of recursive production
(which we want to keep) we cannot always say in advance if a given
piece will ever produce predictions. So we formally allow the existence
of an empty piece of knowledge. Of course, if we can prove that a given
object is an empty piece of knowledge we need not to regard it as
knowledge at all.
A cybernetic system makes predictions in order to achieve certain goal,
ultimately -- survival and proliferation.
True knowledge is an instrument of survival. Knowledge is
power. There is no criterion of truth other than the prediction power it
gives. Since powers, like multidimensional vectors, are hard to
compare, there is no universal and absolute criterion of truth.
Proclamation of any truth as absolute because of being given
through a "revelation" is sheer self-deception.
Formally, a model is a system S = <W, M, E> with:
When the functions L, R, and E commute, then we have m2 = R(m1) = R(E(w1)) =
E(L(w1)) = E(w2). Under these conditions S is a good model,
and the modeling system M can predict the behavior of the world
W. We can call S a generator of predictions about W.
However, it is possible that M is itself a model, in which case S is
a meta-model. The representation function then does not generate
a prediction directly, but rather generates another model, which
in turn can generate predictions. We come, therefore, to the understanding
of knowledge as a hierarchical structure to recursively generate
predictions about the world and the self, and which in turn allow the cybernetic
system to make decisions about its actions.
The difference from modeling is that in homomorphism the operations
are defined on the pairs of elements from the group, while in modeling
the operations are defined on pairs where the first element is
a state of the world or the model, and the second -- an action,
in the world or the model, respectively.
We define a prediction as
a statement that a certain process, referred to as a test
comes to a successful end, i.e.
to a certain, specified in advance, stage, after which
we simply do not care what happens to the process.
The prediction that a test T is successful will be denoted as T!.
We define formally a generalized model as anything
that produces one or more predictions.
When we speak of producing predictions, we have in mind, of course,
some objects that represent predictions, e.g. texts in a certain
language which enable us to reproduce the process that the prediction
is about. The objects representing processes are referred to
as their objectifications (see).
Formally, we can fit our general concept of prediction into the frame
of the modeling scheme, if we even further expand the range of possible
actions a, namely, allow for a being an arbitrary process which may
include both actions of the subject of the model,
and any other actions and processes.
Let the brain of the subject be always found in one of only two states,
let them have the names True and False. The representation
function M_a(w) will result in True if w is the end state of
the process a which succeeded, and False otherwise.
The modeling function M(r) will be universal and very simple:
it immediately produces the object True. Now the model we built makes
exactly one prediction : that the process a ends in success.
A problem can be analysed into more specific components. First of all it consists of the two situations, the present one which we will call the initial state, and the desired one, which we can call the goal state. The agent's task is to get from the initial state to the goal state by means of series of actions that change the state. The problem is solved if such a series of actions has been found, and the goal has been reached. In general, problem-solving is a component of goal-directed action or control.
In simple control problems, the solution is trivial. For example, the thermostat is a control system or agent whose goal is to reach or maintain a specific temperature. The initial state is the present temperature. The action consists in either heating to increase the temperature or cooling to decrease it. The decision which of these two possible actions to apply is trivial: if the initial temperature is lower than the goal temperature, then heat; if it is higher, then cool; if it is the same, then do nothing. Such problems are solved by a deterministic algorithm: at every decision point there is only one correct choice. This choice is guaranteed to bring the agent to the desired solution.
The situations we usually call "problems" have a more complex structure. There is choice of possible actions, none of which is obviously the right one. The most general approach to tackle such processes is generate and test: apply an action to generate a new state, then test whether the state is the goal state; if it is not, then repeat the procedure. This principle is equivalent to trial-and-error, or to evolution's variation and selection. The repeated application of generate and test determines a search process, exploring different possibilities until the goal is found. Searches can be short or long depending on the complexity of the problem and the efficiency of the agent's problem-solving strategy or heuristic. Searches may in fact be infinitely long: even if a solution exists, there is no guarantee that the agent will find it in a finite time.
Such a search process requires a series of actions, carefully selected from a repertoire of available actions to bring the present state closer to the goal. Different actions will have different effects on the state. Some of these effects will bring the present state closer to the goal, others will rather push it farther away. To choose the best action at every moments of the problem-solving process, the agent needs some knowledge of the problem domain. This knowledge will have the general form of a production rule: if the present state has certain properties, then perform a certain action. Such heuristic knowledge requires that the problem states be distinguished by their properties. This leads us to a further analysis of problems.
Problem states will generally involve objects, which are the elements of the situation that are invariant under actions, and properties or predicates, which are the variable attributes of the objects. A problem state then can be formulated as a combination of propositions, where elementary propositions attribute a particular predicate to a particular object. The different values of the predicates determine a set of possible propositions, and thus of possible states. Since states that differ only in one value of one predicate can be said to be "closer" together than states that differ in several values, the state set gets the structure of a space, ordered by an elementary "distance" function. Actions can now be represented as operators or transformations, which map one element of the state space onto another, usually neighbouring, element.
The final component we need to decide between actions is a selection criterion, which tells the agent which of the several actions that can be applied to a given state is most likely to bring it closer to the goal. In the simplest case, an action consists simply of moving to one of the neighbouring states. Each state will then be associated with a certain value which designates the degree to which it satisfies the goal. This value may be called "fitness". The search space then turns into a fitness landscape, where every point in the space ("horizontal") is associated with a "vertical" fitness value, so that a landscape with valleys and peaks appears. Problem-solving then reduces to "hill-climbing": following the path through the fitness landscape that leads most directly upward.
The efficiency of problem-solving is strongly determined by the way the problem is analysed into separate components: objects, predicates, state space, operators, selection criteria. This is called the problem representation. Changing the problem representation, i.e. analysing the problem domain according to different dimensions or distinctions, is likely to make the problem much easier or much more difficult to solve. States which are near to each other in one representation may be far apart in another representation of the same problem. Therefore, a goal state that could be reached easily in one representation may be virtually impossible to find in another one. Problem representations are usually also models of the situation as experienced by the agent.
References:
The most efficient way to find or to construct a model which is adequate
for the given problem is by reasoning on a metacognitive level, where a
class of possible models can be analyzed and compared. This requires a
metasystem transition with respect to the variety of individual models.
Examples of metacognitive reasoning include the Principles of Variety Minimax and of incomplete knowledge.
These principles operate in the context of a metasystem S' = { S_i },
1 < i < n. Typically the S_i are various models,
descriptions, hypotheses, or other knowledge structures. The simplest
measure of the variety of the metasystem S' is given by
|S'| = n, the number of subsystems. Also, each S_i
has its own variety V_i = V(S_i), e.g. a stochastic
entropy.
The principles are:
The Principle of Uncertainty Maximization has a long and venerable
history in inductive reasoning, including Laplace's Principle of
Indifference or Principle of Insufficient Reason and Ockham's razor. It provides guidance in
choosing a specific subsystem S_i from the metasystem
S'.
It can be briefly summarized as follows: in selecting an hypothesis, use no
more information than is available. More technically, given some data
which constrains the hypotheses S_i such that each
S_i is consistent with the data, then choose that hypothesis
which has maximal uncertainty V_i.
The most successful application of the Principle is in stochastic systems,
where it is the Principle of Maximum Entropy (PME). In combination with
Bayesian statistics, the PME has a wide range of important applications as
a general method of inductive inference in science, engineering, and
philosophy of science cite{SKJ89b}. Like the Law or Requisite Variety, under certain
conditions the PME is isomorphic to the 2nd Law of Thermodynamics
cite{JAE57}.
A corresponding Principle of Uncertainty Minimization is a more recent
development cite{CHR80a}. It is less a principle of inductive inference or
system selection than a principle of systems construction, how to construct
a metasystem S' given some systems S_i.
It can be briefly stated as follows: in selecting a metasystem, use all
information available. More technically, given some data and a class S
= { S^j } of sets of hypotheses S^j = { S^j_i }, all of
which are consistent with that data, then let the metasystem S'
be that S^j such that V(S^j) is a minimum. Typically
V(S^j) = |S^j|, but in a stochastic setting it is possible to
consider V(S^j) as a higher order entropy.
Uncertainty Minimization provides a guideline in problem and system
formalization. In particular, it relates to our views on meta-foundationalism. Given a situation where we
have multiple consistent axiom sets
S^j and a requirement to select one, then the Principle should
be invoked.
Like Uncertainty Minimization, this principle is also relatively new,
developed by George
Klir in 1991 cite{KlG93a}. Its use is to guide the scientist when
transforming or translating a system or a problem formulation from one
language or representational frame to another.
It can be briefly stated as follows: when doing such a transformation, aim
to neither gain nor lose any information. This can, of course, be hard to
do if uncertainty and information are represented in different ways in the
different representational frames. Therefore, application of this principle
is highly problem-specific.
For example, uncertainty is measured most generally by the number of
available choices, while in probability theory it is measured by entropy,
and in possibility theory by nonspecificity. Therefore, when moving a
problem formulation from one situation to another, the appropriate measures
should be optimized to be as equal as possible.
More technically, given a system S and the metasystem S' =
{ S_i } of other systems with which we are attempting to model or
represent S, the select that S_i such that
V(S_i) is as close to V(S) as possible.
This principle can be deduced from a lot of other, more specific principles: Heisenberg's uncertainty principle, implying that the information a control system can get is necessarily incomplete; the relativistic principle of the finiteness of the speed of light, implying that the moment information arrives, it is already obsolete to some extent; the principle of bounded rationality (Simon, 1957), stating that a decision-maker in a real-world situation will never have all information necessary for making an optimal decision; the principle of the partiality of self-reference (Lšfgren, 1990), a generalization of Gšdel's incompleteness theorem, implying that a system cannot represent itself completely, and hence cannot have complete knowledge of how its own actions may feed back into the perturbations. As a more general argument, one might note that models must be simpler than the phenomena they are supposed to model. Otherwise, variation and selection processes would take as much time in the model as in the real world, and no anticipation would be possible, precluding any control. Finally, models are constructed by blind variation processes, and, hence, cannot be expected to reach any form of complete representation of an infinitely complex environment.
Second, evolutionary epistemology notes that the individual, ontogenetic development of knowledge is also the result of variation and selection processes, but this time not of whole organisms, but of "ideas" or pieces of potential knowledge. Thus, the typical pattern of scientific discovery is the generation of hypotheses by various means (variation), and the weeding out of those hypotheses that turn out to be inadequate (selection).
This analogy between the creation of ideas and Darwinian evolution has been noted from the end of the 19th century on by different scientists and scholars (e.g. Poincaré and William James). It was first developed into a full epistemology of science by
Campbell's framework rests on three basic ideas:
See also: Gary Cziko's and Donald T. Campbell's extensive
A selector is a system capable of selecting variation. (Thus a
selector can be understood as as agent of will. ) Knowledge
functions as an anticipatory or vicarious selector . A vicarious selector carries selection
out in anticipation of something else, e.g. the environment or "Nature"
at large. For example, molecule configurations selectively retained by
a crystal template are intrinsically stable, and would have been selected
even without the presence of a template. The template accelerates, or
catalyses, the selection, and thus can be said to anticipate, or to vicariously
represent, the naturally selected configuration.
One can also imagine anticipatory selectors making different selections
under different circumstances, compensating different perturbations by
different actions. This kind of anticipatory selection has the advantage
that inadequate internal variations will no longer lead to the destruction
of the system, since they will be eliminated before the system as a whole
becomes unstable. Thus anticipatory selectors select possible actions
of the system in function of the system's goal (ultimately survival) and
the situation of the environment. By eliminating dangerous or inadequate
actions before they are executed, the vicarious selector forgoes the selection
by the environment, and thus increases the chances for survival of the
system.
An vicarious selector can be seen as the most basic form of an anticipatory
control system or indeed of any model. A model is necessarily
simpler than the environment it represents, and this enables it to run
faster than, and thus anticipate, the processes in the environment. It
is this anticipation of interactions between the system and its environment,
with their possibly negative effects, that allows the system to compensate
perturbations before they have had the opportunity to damage the system.
In cases where the different criteria contradict each other, no piece of knowledge can ever optimally fulfill all criteria. We rather need to look for a kind of "Pareto" optimality: different local optima, but such that we cannot combine the advantages of the different candidates into a global optimum that is best for all criteria. Whereas classical theories of knowledge would only recognize two categories of knowledge: true or false, more pragmatic epistemologies would rather order models from "more adequate" (precise, reliable) to "less adequate". In the present framework, this ordering is considered to be partial: it is not alway the case that one model is better than another one, and there is generally no best model. However, there are models which are better than other models and thus the theory avoids any "absolute relativism".
The different criteria can be categorized in three "super" classes:
References:
A related criterion for the reality of perceptions in Gestalt psychology is richness in contrast and detail: imagined or dream perceptions typically are fuzzy and contain little detail.
If the same external phenomenon is
perceived from different angles, distances or illuminations, it will appear
differently, yet maintain some constant distinction or identity. The sensation
produced e.g. by a a particle of dust in the eye, on the other hand, will not
change when the person moves, or will change in a random way, without relation
to the movement of the body.
According to
atribution theory people attribute causes of perceived effects to those phenomena
that covary with the effects, that is to say that are present when the effect
is present, and absent when the effect is absent. To determine whether a
perception is real, you should determine whether its cause is some objective,
external phenomenon, or some internal mechanism (e.g. imagination,
hallucination, malfunctioning of the perceptual apparatus).
Now, external or objective causes will not covary with changes that only
affect internal or subjective variables. For example, some aspects of a perception of an external objects, such as size, and
angle will covary with the movement of the perceiver (internal change). On the
other hand, the fact that something is perceived at all, should not vary with
the location of the observer: it should be invariant over positions. Kelley
(1967) has proposed the following set of criteria that characterize external or
"real" causes of perceptions:
Remark that none of the above criteria is sufficient on its own to establish
the reality of a perception. For example, a mass hallucination or a magician's
illusion may be perceived by thousand people, and hence satisfy criterion b.,
without being caused by an objective phenomenon. A malfunctioning of the eye or
of the nerves may be stable, and hence produce a continuing excitation of the
brain, satisfying criterion a. A hologram can be looked at from different
points of view (criterion c.), but does not correspond to a real object.
Yet, the perception will become more reliable or more real when the different
criteria are fulfilled to a larger degree. The hologram cannot be touched
(different modality), and that gives away its illusory character. The
magician's spectacle may be watched by another magician who would quickly
recognize the trick and expose the illusion. So, all other things being equal,
the larger the number of people agreeing about the perception, the longer it
lasts and the more modalities or points of view through which it is perceived,
the more real it appears, and the more we can rely on it for making
predictions. More generally, the more independent criteria it fulfills, the
more real it will be.
The problem remains to define what "coherence" precisely means: mere consistency is clearly not sufficient, since any collection of unrelated facts is logically consistent. In addition, coherence requires connection and mutual support of the different beliefs. Since learning is based on the strengthening of associations, ideas that do not connect to existing knowledge simply cannot be learnt. Connection means some kind of a semantic or associative relationship, so that information about one idea also gives you some information about the other. An idea can furthermore support another idea by providing an explanation, evidence or arguments why the latter idea should be true. The preference for consistency can be motivated by the theory of cognitive dissonance, which states that people tend to reject ideas that contradict what they already believe. More generally, it follows from the fact that a fit individual must be able to make clear-cut decisions. Mutually contradictory rules will create a situation of confusion or hesitation, which is likely to diminish the chances for survival.
This means that the subject will try to build models which are coherent with the models which it already possesses, or which it receives through the senses or through communication with others. Since models are only compared with other models, the lack of access to exterior reality no longer constitutes an obstacle to further development. In such an epistemology, knowledge is not justified or "true" because of its correspondence with an outside reality, but because of its coherence with other pieces of knowledge (Rescher, 1973; Thagard, 1989).
References:
This "conformity pressure" can be explained by the fact that the newcomer will be subjected to expressions of the idea more often, and will more likely get in trouble if he expresses dissonant idea (Heylighen, 1992). Though conformity pressure is mostly irrational, often rejecting knowledge that is adequate because it contradicts already established beliefs, its alternative formulation, "consensus", is a criterion of the invariance type, since it implies that a belief does not vary over individuals. More invariant rules are more reliable predictors, and consensus, in the sense where people agree about an idea because they independently came to the same conclusion, can be viewed as a quite rational criterion for selecting knowledge (cf. Kelley, 1967).
From another point of view, conformity is an expression of "meme selfishness" (Heylighen, 1992). As memory space is limited and cognitive dissonance tends to be avoided, it is
difficult for inconsistent memes to have the same carriers. Cognitively
dissonant memes are in a similar relation of competition as alleles: genes that
compete for the same location in the genome. Memes that induce behavior in
their carriers that tends to eliminate rival memes will be more fit, since they
will have more resources for themselves. The concrete result is that a group of
carriers with different memes will tend towards homogeneity, resulting from the
imposition of the majority meme and elimination of all non-conforming memes.
Conformity is a necessary criterion for the evolution of cooperation, that is, for the selection of behaviors that are collectively useful, without being individually useful. As D. T. Campbell emphasizes, group selection often runs counter to the more powerful and direct force of individual selection. Therefore, he proposes a mechanism that suppresses individually selfish deviations from these collective beliefs: conformist transmission. As illustrated by the mathematical model of Boyd and Richerson (1985), all other things being equal, it seems evolutionarily optimal for subjects to adopt the majority or plurality belief rather than a minority idea. Thus, already popular ideas tend to become even more popular, leading to an eventual homogeneity of belief within a closely interacting group.
References:
The integration on the level of norms and codes fostered by conformity and the differentiation on the level of expertise fostered by authority together produce a complexification of the social system. The process is similar to the metasystem transition which produced the differentiated organs and tissues in a multicellular organism. Thus, it leads to the further devlopment of a social superorganism.
That construction serves in the first place selfish purposes: the subject wants to get control over what it perceives, in order to eliminate any deviations or perturbations from its own preferred goal state. Control requires a model of the thing to be controlled, but that model will only include those aspects relevant to the subject's goals and actions. In a sense, the subject does not care about the "thing" to be controlled, only about compensating the perturbations it senses from its goal, thus being able to adapt to changed circumstances.
Constructivist mechanisms are not limited to higher level learning or discovery of models, they pervade all evolutionary processes. The difference between Lamarckian and Darwinian evolutionary theory is just that Lamarck assumed that the environment somehow instructs an organism on how to be adapted. Darwin's view emphasized that an organism has to find out for itself, by trial and error. A similar conceptual transition from instruction to construction took place in the theories of immunity: the organism is not instructed in any way how to produce the right antibodies to stop the invaders, as was initially believed, it needs to generate all possible combinations by trial-and-error until it finds a type of antibody that works. Once such an antibody is discovered, the "knowledge" about how to fight that particular infection remains, and the organism becomes immune. The conceptual development from instructionism to selectionism or constructivism is well-described in Gary Cziko's book
Since constructivism rejects any direct verification of knowledge by comparing the constructed model with the outside world, its most important issue is how the subject can choose between different constructions to select the "right one". Without such a selection criterion, constructivism would lapse into absolute relativism: the assumption that any model is as adequate as any other. The two most often used criteria are coherence, agreement between the different cognitive patterns within an individual's brain, and consensus, agreement between the different cognitive patterns of different individuals. The latter position leads to "
See also:
Compare our cybernetic epistemology with the classical
reflection-correspondence theory of meaning and truth.
One of the oldest questions of philosophy is: What is the meaning of
words and phrases of a language? The naive answer is: those
things which the words denote. This is known as the reflection
theory of language. Language, like a mirror, creates certain
images, reflections of the things around us. With the reflection
theory of language we come to what is known as the correspondence
theory of truth: a proposition is true if the relations between
the images of things correspond to the relations between the
things themselves. Falsity is a wrong, distorted reflection. In
particular, to create images which correspond to no real thing in
the world is to be in error.
With this concept of meaning and truth, any expression of
our language which cannot be immediately interpreted in terms of
observable facts, is meaningless and misleading. This viewpoint
in its extreme form, according to which all unobservables must be
banned from science, was developed by the early nineteenth-century
positivism (Auguste Comte). Such a view, however, is
unacceptable for science. Even force in Newton's mechanics
becomes suspect in this philosophy, because we can neither see nor
touch it; we only conclude that it exists by observing the
movements of material bodies. Electromagnetic field has still less of
reality. And the situation with the wave function in quantum
mechanics is simply disastrous.
The history of the Western philosophy is, to a considerable
extent, the history of a struggle against the
reflection-correspondence theory.
We now consider language as a material to create
models of reality. Language is a system which works as a whole,
and should be evaluated as a whole. The job the language does is
organization of our experience, which includes, in particular,
some verifiable predictions about future events an the results of
our actions. For a language to be good at this job, it is not
necessary that every specific part of it should be put in a direct
and simple correspondence with the observable reality.
Unlike our dynamic concept of modeling as production of predictions,
the classical concept of reflection is static.
It immediately raises the questions like what does it actually mean
that one thing "reflects" another. Also, how do we know that
reflection takes place? To confuse things further, a distinction
between mind and matter was made, which produced the question:
how our ideas, belonging to mind, can reflect objects belonging to
the realm of matter.
The cybernetic understanding of knowledge is much more precise.
This precision is achieved by introducing dynamics into the picture.
The mapping form the world to language present in the homomorphism picture
is not required to be a "reflection"; we need not compare these two
strata of reality. To see that the model works, we only have to compare
things from the stratum of language.
All that has been said about language can be applied also to human thought.
In cybernetic view, thought works because it implements some models
of the world, not because it somehow statically reflects it. The difficult
questions of the correspondence between the thought and its object
simply do not arise.
In a static world no knowledge, no reflection or correspondence
would be possible. Correspondence make sense only if we indicate
a procedure which establishes what we want to call correspondence;
and a procedure inescapably includes a time dimension.
Knowledge is both objective and subjective because it
results from the interaction of the subject (the cybernetic system)
and the object (its environment). Knowledge about an object is
always relative: it exists only as a part of a certain subject.
We can study the relation between knowledge and reality (is the
knowledge true or false, first of all) if the subject of
knowledge, a cybernetic system S , can become part of a metasystem S'
in whose terms the knowledge about S and its relation to reality
can be expressed.
The metasystem transition from S to S' generates
a new type of knowledge. It is of the same nature as the
metasystem transition from using a tool to making a new kind of
tool, "metatools" , which serve to produce and improve tools. A
We can study the relation between knowledge and reality: first of all,
whether a piece of knowledge is true or false. For that purpose
the subject of knowledge, a cybernetic system S, must become part
of a metasystem S' in whose terms the knowledge of S and its relation
to reality can be expressed. But this only makes the knowledge relative to
the system S'. This kind of metasystem transition may be repeated
many times, resulting, possibly, in
ever deepening knowledge, but at any time the knowledge will be
still relative to a definite cybernetic system, for
which it is a model used for obtaining predictions: nothing more,
nothing less. The cybernetic concept of knowledge features
an organic unity of the object and the subject of knowledge.
Some philosophers of the 19th century started reasoning with
the distinction between "I" and "not-I"as the most primordial
and self-evident fact of being. This sounded metaphysical
and unnecessary to contemporary scientists, because they
thought about the world as existing independently of my "I",
and about their descriptions of the world's phenomena as completely
objective. My "I" was simply part of the world, as well as your "I"
and his "I".
The development of physics, however, demanded a careful attention
to the process of obtaining our knowledge. The "I" crept into science
as the observer of Einstein's relativity and the experimenter of quantum
mechanics. We often speak of a reference system instead of the observer,
and a measuring device instead of the experimenter, but this is a futile
attempt to ban "I". A reference system and a measuring device are only
ways to describe the activity of "I".
With the cybernetic notion of knowledge and meaning, "I" is firmly
built into knowledge.
The following metaphor may help understand it. Knowledge is a tool.
Each tool has a handle which you grasp when you use it. Different
people (or even creatures from other planets) may use the same tool,
but whenever it is used, somebody grasps the handle, and this is the "I"
of knowledge, meaning and truth.
In the cybernetic foundation of mathematics [...] we show that if
we start with the
principle that a meaningful mathematical proposition is a generator
of predictions, we come to the necessity of introducing the user of
the mathematical tools into the formalism. The tools of mathematics
do not work autonomously, like Turing machines, but rather in an interactive
mode. The user of such machines is, like Einstein's observer, a form
of "I".
Semantic analysis discovers "I" in some of our most important
notions. Take causality. What do we mean by saying that A causes B?
We cannot observe this relation between phenomena. We can observe only
a time sequence "B after A", but this may be two consequences of a
common cause, or just a coincidence. The real meaning of the statement of
causality includes my freedom to allow or not to allow A happen,
to choose between A and not-A.
Then the meaning of "A causes B" is: if I allow A happen, B will
take place too, but if I do not allow A, B will not take place.
This is a meaningful proposition, a model of reality; but this model
inextricably includes "I". To test causality, there must
be a freedom to allow or not to allow A. "I" is the only source
of this freedom. (See Causality for more detailed treatment.
The theory of probability relies heavily on "I". Recall the old paradox:
we believe that events with probability zero (or vanishingly small)
cannot happen. Meanwhile, every event that happens has the probability
zero. The error here is thinking in terms of "objective reality".
Probability is not an objective attribute of events. It is an instrument
of decision taking, thus it becomes completely meaningless if there is
nobody there to take decisions. Probability describes a relation between
the subject of knowledge, "I", who now appears as a decision maker,
and various events. Before an event we can speak of its probability,
and it may be very small. After it took place, we cannot speak of its
probability, because in decision taking we consider future, not past,
events.
We often use the words "intuition", "intuitively", meaning
some act of our thought which cannot be decomposed into any constituting
elements and, in particular, cannot be further explained or justified.
This is the result of activating some non-verbal model of the world
implemented in our brain. Sometimes we are very certain about what our
intuition tells us; on other occasions we found ourselves in the state
of doubt.
Doubt is a result of having in the mind more than one models applicable
to the current situation. Some of our brain models are built-in
from birth, or develop in a short time after the birth. We can hypothesize
that such models tend to be applicable in a unique way, so they do not
invoke doubt. Other models develop in the process of life and are determined
by our experience. It may well be that at different times two or more
non-verbal models were developed which can be applied in the current
situation. We perceive this as doubt. This meaning of the word 'doubt'
is reflected in its etymology. 'Doubt' is, apparently descending from
'double', meaning a double opinion. In the Russian language the word for
doubt is 'somnenie', which breaks down as 'so-mnenie', literally
co-thought, a parallel thought.
A language is a convention according to which certan material objects,
to be referred to as linguistic objects, define certain actions,
which are referred to as their meanings. There are two basic types
of linguistic objects: commands and statements.
Commands are used in the context of control, where the meaning
of a command issued by the controlling system is the resulting action
of the controled system. The meaning of a statement is the piece
of knowledge (true or false), that is a hierarchical generator
of predictions.
Human language is a multilevel system.
On the lower levels, which are close to
our sensual perception, our notions are almost in one-to-one
correspondence with some conspicuous elements of perception.
In our theories we construct higher levels of language. The concepts
of the higher levels do not replace those of the lower levels, as
they should if the elements of the language reflected things "as
they really are", but constitute a new linguistic reality, a
superstructure over the lower levels.
Predictions produced by the higher levels are formulated in terms
of the lower levels. It is a hierarchical system, where the top
cannot exist without the bottom.
We loosely call the lower-level concepts of the linguistic
pyramid concrete, and the higher-level abstract. This is a very
imprecise terminology because abstraction alone is not sufficient
to create high level concepts. Pure abstraction from specific
qualities and properties of things leads ultimately to the lost
of contents, to such concepts as `something'. Abstractness of a
concept in the language is actually its `constructness', the
height of its position in the hierarchy, the degree to which it
needs intermediate linguistic objects to have meaning and be
used. Thus in algebra, when we say that x is a variable, we
abstract ourselves from its value, but the possible values
themselves are numbers, which are not `physical' objects
but linguistic objects formed by abstraction present
in the process of counting. This intermediate linguistic level of
numbers must become reality before we use abstraction on the next
level. Without it, i.e. by a direct abstraction from countable
things, the concept of a variable could not come into being.
In the next metasystem transition we deal with abstract algebras,
like group theory, where abstraction is done over various operations.
As before, it could not appear without the preceding
metasystem level, which is now the school algebra.
There is another parameter to describe concepts of a language.
This is the degree to which the language embedding the concept or
concepts is formalized. A language is formal, or formalized, if
the rules of manipulation of linguistic objects depend only on
the `form' of the objects, and not on their `human meanings'. The
`form' here is simply the material carrier of the concept, i.e. a
liguistic object. The `human meaning' is the sum of associations it
evokes in the human brain. While `forms' are all open for
examination and manipulation, i.e. are objective,
`human meanings'are subjective, and are communicated indirectly.
Operations in formal languages can be delegated to mechanical devices,
machines. A machine of that kind becomes an objective model of reality,
independent from the human brain which created it. This makes it
possible to construct hierarchies of formal languages, in
which each level deals with a well-defined, objective reality of
the previous levels. Exact sciences operate using such hierarchies,
and mathematics makes them its object of study.
Classification of languages by these two parameters leads
to the following four types of language-related activities :
Art is characterized by unformalized and concrete language.
Words and language elements of other types are important only as
symbols which evoke definite complexes of mental images and
emotions. Philosophy is characterized by abstract informal thinking.
The combination of high-level abstract constructs used in
philosophy with a low degree of formalization requires great
effort by the intuition and makes philosophical language the most
difficult type of the four. Philosophy borders with art when it
uses artistic images to stimulate the intuition. It borders with
theoretical science when it develops conceptual frameworks to be
used in construction of formal scientific theories. The language
of descriptive science must be concrete and precise;
formalization of syntax by itself does not play a large part, but rather
acts as a criterion of the precision of semantics.
A message is an object which has some meaning
for some agent.
A symbol is the maximal unit (subsystem) of a language which can
never be broken into parts. For instance, with natural human languages
the morphemes (such as word roots, prefixes,
prepositions etc.) play the role of symbols. In programming languages
the symbols are usually referred to tokens.
A sentence is the minimal unit of a language which can have a meaning
of its own, in separation from the rest of the message. Very often
a message of a language is a sequence or a tree of sentences.
Sentences of natural human languages are, with some reservations
(e.g. concerning the use of pronouns) sentences in our formal sense.
In programming languages sentences are usually called statements;
this is in disagreement with the wide use of the term statement
as denoting some description of a situation, like a proposition
in logic. It is this wiser usage that we catch in our formalization of
statement. Statements of programming languages are,
in our terminolgy, commands (see).
Often the syntax of a language is defined by a non-deterministic
procedure G which produces all legitimate meassages. Then the procedure
which for any given object decides whether it could be produced by G,
and if it could then by which steps of G, is known as parsing.
Our definition of knowledge allows us to further define meaning and truth.
When we say or write something we, presumably, express our knowledge.
By the definition of a message, it must have a meaning. But what is
meaning?
First of all, messages are always addressed to a certain agent.
Also, they are supposed to influence the actions performed by this agent,
otherwise there would no sense in producing and passing the message.
We know of exaclty two ways of changing the actions of an agent.
One way is to change the state of the world as far as the agent is
concerned. The other way is to change the agent's model of the world
(if any). Thus by the type of their semantics messages of a language
break into two categories: commands and statements.
A command is a message which directly changes the state of the world
as far as the receiver of the message is concerned, i.e. the set
of possible actions for it.
Changing the state of the world the sender of a command can prevent the
receiver from doing something or open a possibility of doing
something new. The meaning of
a command is the way it changes the state of receiver. In the classical
limiting case a command leaves the receiver no choice at all, so that
the action of the receiver is uniquely determined by the command.
Computer languages can serve as an illustration of this kind of semantics.
Another example is control of a rocket from the earth. It involves
a certain language of electromagnetic signals sent to the rocket.
Here the command leaves almost no choice for the rocket,
because there is no absolute precision of the implementation of continuous
quantities. This situation is typical; what is meant by 'almost' is,
of course varying from case to case.
Thus to be meaningful, a sentence must meet the same requirement as a piece of knowledge:
we must know how to be able to produce predictions from it, or produce
tools which will produce predictions, or produce tools to produce such
tools, etc. If we can characterize the path from the statement to
predictions in exact terms,
the meaning of the statement is exact. If we visualize this path
only vaguely, the meaning is vague. If we can see no path from a
statement to predictions, this statement is meaningless.
We do not identify meaningless with worthless. Since our criterion
of the meaningful includes a reference to the process of deriving
predictions, the meaning is to some extent subjective, and what is
meaningless for one person may be meaningful for another.
Furthermore, seemingly meaningless statements may lead to --
through some mysterious processes in our brain -- new ideas and
discoveries.
Our criterion of the meaningful should be used as a guide for making
our ideas more clear and precise, not as a reason for categorical
rejections.
Our definition of meaning as potential knowldge assigns meaning only
to messages, but not to their parts. Yet parts also have some meaning;
we do not say that the word 'table' is meaningless. It has a meaning,
but of its own kind, which we shall designate as instrumental,
because it is used in assignin meaning to such sentences as
'This is John's table', or 'My table is is made of metal'. The preposition
'in' also has an instrumental meaning: it is used to construct such
sentences as 'There is an apple in this box'. Usually it is clear
from the context which kind of meaning we mean. One exception is our
definition of a message as the minimal unit of the language that has
a definite meaning. We must make it clear that we have in mind
meaning proper, not instrumental meaning.
If we understand the instrumental meaning of a word, we can describe
how precisely it is used in models. Since to describe models we have to
describe processes which they involve, a description of instrumental
meaning will, probably, also involve the description of cerain processes.
For example, the meaning of such a noun as 'table' is in the abstraction
process which recognizes an object as a table. This process is must be
inevitably used in the meaning of any sentence including the word 'table'.
A concept is any part of language which has an instrumental
meaning. In human language we distinguish neuronal and logical
concepts (see Human language).
The vertical lines in the modeling scheme are functions, or mappings
R from the states of the world w_i to their representations r_i
(the states of
the brain of the subject system S). This mapping is always
an abstraction: some aspects of the state of the world are necessarily
ignored, abstracted from, in the jump from reality to its description.
The role of abstraction is very important: it reduces the amount of
information the system S has to process before decision making.
The term abstract concept or simply concept is often used,
and will be used here, as asynonym of abstraction.
We often use the same word to denote both a process and its result.
Thus all representations r_i resulting from mapping are also referred
to as abstractions. We may say, for instance, that triangle is
an abstraction from all specific triangles.
It should be kept in mind, however, that abstraction, or an abstract concept,
is not so much a specific representation (such as a language object),
as the procedure which defines what is ignored and what is not ignored in
the mapping. Obviously, the object chosen to carry the result of abstraction
is more or less arbitrary; the essense of the concept is in the
procedure that transforms w_i into r_i.
Given a representation function R and a specific representation r,
we can construct a specialized function which will recognize the fact
that a given state of the world w belongs to the abstraction r.
We define this function as follows:
P_r(w) = True if R(w) = w,
False if R(w) =/ w.
Here True and False are two symbols chosen to represent two possible
results of the function. Such functions as P_r are known as
predicates (see). The predicate P_r(w) takes the value True
for those and only those states w which are represented by r.
Whenever we speak of a predicate, we can also speak of a set, namely, the
set of all states of the world w for which the predicate is true (takes
the symbol True as its value). We shall call this set the scope
of the abstract concept. Sometimes it is convenient to define an
absraction through its scope, e.g., a member of John Smith's family
can be defined by simple enumeration. But the universal way is the
definition by property, in which case a reformulation through a set does
not clarify the concept. If we "define" abstract triangle as the set of all
specific triangles, it still remains to define what a specific triangle is.
The real definition of an (abstract) triangle is a predicate,
a procedure which can distinguish a triangle from everything else.
A cybernetic system may be interested, depending on its current purposes,
in different parts, or aspects, of reality. Breaking the single
all-inclusive state of the world w_i into parts and aspects is one of the
jobs done by abstraction. Suppose I see a tea-pot on the table,
and I want to grasp it. I can do this because I have in my head
a model which allows me to control the movement of
my hand as I reach the tea-pot. In this model, only the position and
form of the tea-pot is taken into account, but not, say the form of
the table, or the presence of other things, as long as they do not
interefere with grasping the tea-pot. In another
move I may wish to take a sugar-bowl. Also, I may be aware that
there are exactly two things on the table: a tea-pot and
a sugar-bowl. But this awareness is a result of my having two distinct
abstractions: an isolated tea-pot and an isolated sugar-bowl.
The degree of abstraction can be measured by two parameters:
its scope and level; correspondingly, there are two ways
to increase abstraction.
The scope was defined above. The wider the scope of a concept, the more
abstract it is. The classical example is: cats, predators, mammals, etc.
up to animal. With this method, the content of the concept (i.e. the amount
of specificity in its procedural definition) decreases as the degree
of abstraction increases. We come finally to such universal abstractions
as object or process which carry almost no information.
The level of an abstraction is the number of metasystem transitions
(see) involved. In the modeling scheme the sibject-of-knowledge system S
is a metasystem with respect of the world. Indeed, S {\controls} the
world: it takes information from the world as input to create
representation using R, processes it using M_a for various a,
chooses a certain action a, and executes it at the output, changing
thereby the state of the world. The brain of S, as the carrier of
world representations, is on the metalevel, a 'metaworld', so to say.
Assigning to the world level 0, we define the abstractions implemented
in the brain as abstractions of the first level.
However, the creation of models of reality does not necessarily end with
the first level abstractions. The brain of the level 1 can become the world
for the new brain, the brain of the level 2. Naturally, the necessary
machinery comes with it -- the second metasystem transition has taken
place. Our human brain is known to have a many-level hierarchical
structure. The "brain" of the first level is nothing but our sense organs.
The eye contains the retina and the machinery necessary to through light
on it and create representations of the world. The retina keeps
first level abstractions and serves as the input for the next level
of the brain hierarch whose representations will be abstractions of
of the second level, etc.
The concept of number can serve as an example of an abstraction of
the second level implemented in human language. Specific numbers are
first-level abstractions. We derive them directly from our experience.
The representation function for this model (arithmetic) is counting.
The brain (in our technical sense) includes some physical carrier
to keep specific numbers, such as an abacus, or paper and pencil.
A specific number, say three is an abstraction from three apples, or
three sheep, etc., whatever we are counting. The concept of a number
is an abstraction from one, two , three, etc., which all are abstractions
themselves which exist only in the first-level brain, and if not that brain,
would not be found anywhere.
Another important example of a concept of the second level of abstraction
is system (see).
Abstractions of the second and higher metasystem levels will also be called
conceptual schemes.
In algebra the second-level abstraction number becomes a material for
higher abstractions, and this metasystem transition can be repeated
many times. When we say that the concepts used in mathematics
or philosophy are very
abstract, we should realize that this high degree of abstraction comes not
from the increase in scope, but increase in the level.
We constract a language which is, like our brain, a multilevel
hierarchical system. High level of abstraction goes in step with the high
level of construction.
===============
!!! Abstraction breaks the world into parts by ignoring something
but including something else. This refers to processes, not only
to objects. In fact, the only possibility to define what is process
(informally -- a part of the world) is to refer to an abstraction
mechanism: what is left is a process, what is abstracted away is not
this process, but "other processes"
\eon
\eon
Our language is a multilevel system. On the lower levels, which are close
to our sensual perception, our notions are almost in one-to-one
correspondence with some conspicuous elements of perception. In
our theories we construct higher levels of language. The concepts
of the higher levels do not replace those of the lower levels, as
they should if the elements of the language reflected things "as
they really are", but constitute a new linguistic reality, a
superstructure over the lower levels. We cannot throw away the
concepts of the lower levels even if we wished to, because then
we would have no means to link theories to observable facts.
Predictions produced by the higher levels are formulated in terms
of the lower levels. It is a hierarchical system, where the top
cannot exist without the bottom.
We loosely call the lower-level concepts of the linguistic
pyramid concrete, and the higher-level abstract. This is a very
imprecise terminology because abstraction alone is not sufficient
to create high level concepts. Pure abstraction from specific
qualities and properties of things leads ultimately to the lost
of contents, to such concepts as something. Abstractness of a
concept in the language is actually its `constructness', the
height of its position in the hierarchy, the degree to which it
needs intermediate linguistic objects to have meaning and be
used. Thus in algebra, when we say that x is a variable, was
abstract ourselves from its value, but the possible values
themselves are numbers, i.e. linguistic objects formed by abstraction
in the process of counting. This intermediate linguistic level of
numbers must become reality before we use abstraction on the next
level. Without it, i.e. by a direct abstraction from countable
things, the concept of a variable could not come into being.
There is another parameter to describe logical concepts.
This is the degree to which the language embedding the concept or
concepts is formalized. A language is formal, or formalized, if
the rules of manipulation of linguistic objects depend only on
the `form' of the objects, and not on their `meanings'. The
`form' here is simply the material carrier of the concept, i.e. a
word, an expression. The `meaning' is the sum of association it
evokes in the human brain. While `forms' are all open for
examination and discrimination, i.e. objective, `meanings'
are subjective, and are communicated indirectly.
Operations in formal languages can be delegated to mechanical devices,
machines. A machine of that kind becomes an objective model of reality,
independent from the human brain which created it. This makes it
possible to construct hierarchies of formalized languages, in
which each level deals with a well-defined, objective reality of
the previous levels. Exact sciences operate using such hierarchies,
and mathematics makes them its object of study.
Classification of languages by these two parameters leads
to the following four types of language-related activities
(I take the table from by book The Phenomenon of Science):
{\begtt
~ Concrete language Abstract language
~
~
Unformalized Art Philosophy
language
~
~
Formalized Descriptive Theoretical
language sciences sciences,
~ mathematics
\endtt}
Art is characterized by unformalized and concrete language.
Words and language elements of other types are important only as
symbols which evoke definite complexes of mental images and
emotions. Philosophy is characterized by abstract informal thinking.
The combination of high-level abstract constructs used in
philosophy with a low degree of formalization requires great
effort by the intuition and makes philosophical language the most
difficult type of the four. Philosophy borders with art when it
uses artistic images to stimulate the intuition. It borders with
theoretical science when it develops conceptual frameworks to be
used in construction of formal scientific theories. The language
of descriptive science must be concrete and precise;
formalization of syntax by itself does not play a large part, but rather
acts as a criterion of the precision of semantics.
\eon
\eon
A piece of knowledge is true if the predictions made by the subject
(the user) of knowledge on the basis of this knowledge are true.
A prediction that test T is successful (denoted as T!) is true
if the test T is, in actual fact, successful.
What this definition says is, essentially, that for every statement S
the statement 'S is true' is true if and only if S itself is true.
We call such statements equivalent.
But equivalency is not a tautology; the meanings of these two statements are
different, even though they always are either both true or both false.
To see this clearly we want to make more formal the system aspect
of our definition.
Statements of a language represent some pieces of knowledge which
can be reconstructed from statements by the recipient of the message.
(which may be the sender of the message itself).
These pieces of knowledge produce, ultimately, some predictions:
T_1!, T_2!, ... etc. that certain tests are successful.
Knowledge about the world constitutes a metasystem with respect
to the world in which the tests T_1, T_2, ... etc. take place.
When we speak of statements and determine their various properties,
we create one more metasystem level; this is a metasystem transition.
While the first level is the level of
the use of knowledge, the second level is that of the analysis
and evaluation of knowledge.
Generally, the construction of a new
level of analysis and evaluation may be extremely fruitful and
all-important. What we usually want are efficient procedures to decide
whether statements are true or false. But as long as the semantics of
truth statements goes, the results are more modest.
The informal meaning of the statement 'S is true' is that some
correct process of analysis of S concludes that S is true.
Obviously, an attmept to define what is correct will lead us back
to the concept of truth. Our definition avoids this loop
by reducing 'S is true' to S. But if somebody insists on defining
a correct process of evaluation, then the definition will be as
follows. The evaluation process, when applied to a statement, is correct
if it results in the value 'true' if and only if it results in 'true'
when evaluating all predictions generated by this statement.
When applied to a prediction T!, the correct evaluation process must
result in 'true' if and only if the test T is successful.
This definition is a reformulation of our original definition of truth.
The metasystem staircase does not, of course, end with the second level.
We can create the third metasystem level
to decide whether the statement 'S is true' is true, an so on infinitely.
But if we only mean the semantics of it, then it is not worthwhile to do.
Even though formally different, all these statements will be
equivalent to each other.
We shall go along with the common understanding of the true and the false
according to which what is not true is false, and vice versa.
Now we put the question: What does it mean that a statement is false?
To be meaningful, the statement of falsehood must be, as any other
statement, interpreted as a prediction or a recursive generator of
predictions. Let us start with the case of prediction.
Consider a prediction T!. If it is not true, there are two possibilities:
that test T ends in failure, and that it never ends at all.
The statement of the end in failure is an ordinary prediction: T runs,
stops, we compare the result with Failure and this comparison succeeds.
But what about the case when T never ends, i.e. is the statement that
T is infinite?
The statement that a certain process is infinite is not a prediction.
But it is a generator of predictions. Our definition of a prediction T!
includes a procedure, let it be denoted as P(t_i), which
is applied to the states t_i, i= 1,2,... etc. of the test T
and determines, in a finite time, whether each given
state is Success, Failure, or neither of
the two, which we shall denote as Not-end. Therefore, the statement
that the state t_i is Not-end is a prediction, namely,
the success of the procedure that runs P(t_i) and compares the result
with Not-end. Now we can define what is the meaning of the statement
that T is infinite: it is a generator which produces the following
row of predictions:
t_1 is Not-end
t_2 is Not-end
t_3 is Not-end
...
etc., infinitely
\eon
We easily agree that test is either finite
or infinite. Now that we have the exact meaning of being infinite,
we can formulate this assumption in its exact form.
We postulate and consider it self-evident that a test is either finite
or infinite. This excludes any third, or middle, possibility,
which gave this principle the name of the law of the excluded middle.
From this we derive that a prediction may be only true or false.
We further derive the law of the excluded middle for arbitrary
statements. Consider some statement S which is a generator of predictions.
Let us run this generator and define the following refutation process.
Each time that a prediction if produced it it replaced by the symbol
True if it is true and False if it is false.
The first time the symbol False appears in the refutation process,
the process ends and succeeds. This process is either finite, or infinite.
If it is infinite, the statements S is true, otherwise it is false.
No other outcome is possible.
\eon
Now that we know that a statement is either true or false, we want to
classify them correspondingly. This is done through predicates.
We call predicate an agent which examines a statement and the world
about which the statement is, i.e. the world of the tests
T_1, T_2, ... etc.,
and comes with one of the two outputs:
True if the statement is true, or False if false.
The symbols True and False are referred to as truth values.
Predicates are abstractions of the second level (see abstraction.
In some cases we can construct predicates as machine procedures,
in other cases a person or a group of persons may work for a long time
in order to come with an answer.
In a wider sense, a predicate is any function which takes one of the two
truth values. Such a function is understood as taking the input values,
constructing a statement from them, and evaluating the truth value of this
statement.
\eon
Up to know we have been speaking of truth in abstraction from the actual
means we have to establish the truth of a statement.
The most general term for establishing the truth of a statement
is proof.
By proof of a statement S we mean any process which the subject
of knowledge accepts as the evidence that S is true and is ready to
use S for predictions on the basis of which to make decisions.
There are two cases of proof which can never arise any doubt because
they do not base on any assumptions: verification and
direct refutation.
Verification is a direct use of the definition of truth to decide if
the statement is true.
Predictions are, in principle, verifiable. You only have to initiate the
test process that the prediction is about and wait until it comes to the
final state. Thus, if a prediction is correct, there is, in principle,
a way to verify this, even though it may require such a huge time, that in
practice it is impossible.
Now consider the situation when you want to verify a prediction T!,
but the test process T is infinite.
This means that the prediction is false, but you will never be able
to verify this directly. To sum up, the following three cases are
possible when we try to verify a prediction:
Testing process Prediction is
-------------------- -----------------
1. ends in success verifyably true
2. ends in failure verifyably false
3. never ends false, but this is not directly verifyable
As to the verififcation of general statements (generators of predictions),
it may be possible only if the number of prediction produced is finite.
In the more usual case, with an infinite number of prediction produced,
the direct verification is impossible.
\eon
A general statement which may produce an unlimited number of predictions
can never by directly verified. But it may be directly refuted,
i.e. found to b false. This happens when it produces a prediction T!,
but in fact the test T ends in failure.
What we call theories are general statements which may produce
infinite number of specific predictions. Theories are not directly
verifiable, but they may be refuted.
\eon
When a statement cannot be directly verified or refuted, it is still
possible that we take is as true relying on our intuition.
For example, consider a test process T the stages of which can be
represented by single symbols in some language.
Let further the process T develop in such
a manner that if the current stage is represented by the symbol A, then
the next stage is also A, and the process comes to a successful end
when the current stage is a different symbol, say B. This definition
leaves us absolutely certain that T is infinite, even though this cannot
be either verified, or refuted. In logic we call some most
immediate of such statements axioms and use as a basis for
establishing the truth of other statements. In natural sciences
some of the self-evident truths serve as the very beginning of the
construction of theories.
\eon
\eon
...
\eon
We distinguish between factual statements and theories. If
the path from a statement to verifiable predictions is short and
uncontroversial, we call it factual. A theory is a statement
which can generate a wide scope of predictions, but only through
some intermediate steps, such as reasoning, computation, the use
of other statements. Thus the path from a theory to predictions
may not be unique and often becomes debatable. Between
the extreme cases of statements that are clearly facts
and those which are clearly theories there is a whole
spectrum of intermediate cases.
Top-level theories of science are not deduced from
observable facts; they are constructed by a creative act, and their
usefulness can be demonstrated only afterwards. Einstein wrote:
"Physics is a developing logical system of thinking whose
foundations cannot be obtained by extraction from past experience
according to some inductive methods, but come only by free fantasy".
The statement of the truth of a theory has essentially the
same meaning as that of a simple factual judgment: we refer to
some experience which justifies, or will justify,
the decision-making on the basis of this statement.
When this experience is in
the past we say that the truth is established.
When it is expected in the future we say it is hypothetical.
There is no difference of principle between factual
statements and theories: both are varieties of models of reality which
we use to make decisions. A fact may turn out to be an illusion,
or hallucination, or a fraud, or a misconception. On the other
side, a well-established theory can be taken for a fact. And we
should accept critically both facts and theories, and re-examine
them whenever necessary. The differences between facts
and theories are only quantitative: the length of the path
from the statement to the production of predictions.
\eon
\eon
The vertical lines on the scheme of modelling are functions, or mappings,
from the states of the world W to representations R (the states of the
language L of the model). This mapping is always
an abstraction: some aspects of the state of the world are necessarily
ignored, abstracted from, in the jump from reality to its description.
The role of abstraction is very important: it reduces the amount of
information the system S has to process before decision taking.
The simplest case of abstraction, mathematically,
is when the states of the world wi
are described by a set of variables w1,w2,...,wn, and we can separate
those variables, say w1,W2,...,wm, on which M really depends,
from the remaining variables wm+1,...,wn,
on which it does not really depend, so that
M(w1,w2,...,wm,x{m+1},...,wn) = M'(w1,w2,...,wm)
We often use the same word to denote both a process and its result.
Thus all representations ri resulting from mapping will be also referred
to as abstractions. It should be kept in mind, however, that abstraction
is not so much a specific representation (a linguistc object),
as the procedure M which defines what is ignored and what is
not ignored in the mapping.
Obviously, the object chosen to carry the result of abstraction
is more or less arbitrary; the essense of the concept is in the
transformation of wi into ri.
Mathematically, an abstraction ri can be defined as the set of all
those states of the world w which are mapped on ri. i.e. the
set of all w such that M(w) = ri. The abstraction 'tea-pot' is the set
of all those states s in S which are classified as producing
the image of a tea-pot on the retina of my eyes.
A cybernetic system, depending on its current purposes, may be
interested in different parts, or aspects of reality. Breaking the single
all-inclusive state of the world wi into parts and aspects is one of the
jobs done by abstraction. Suppose I see a tea-pot on the table,
and I want to grasp it. I can do this because I have in my head
a model which allows me to control the movement of
my hand as I reach the tea-pot. In this model, only the position and
form of the tea-pot is taken into account, but not, say the form of
the table, or the presence of other things on it. In another
move I may wish to take a sugar-bowl. And there may be a situation where
I am aware that there are exactly two things on the table: a tea-pot and
a sugar-bowl. But this awareness is a result of my having two distinct
abstractions: an isolated tea-pot and an isolated sugar-bowl.
The other aspect of abstraction results from the hierarchical nature of
our language.
We loosely call the lower-level concepts of the linguistic
pyramid concrete, and the higher-level abstract. This is a very
imprecise terminology because abstraction alone is not sufficient
to create high level concepts. Pure abstraction from specific
qualities and properties of things leads ultimately to the lost
of contents, to such concepts as `something'. Abstractness of a
concept in the language is actually its `constructness', the
height of its position in the hierarchy, the degree to which it
needs intermediate linguistic objects to have meaning and be
used. Thus in algebra, when we say that x is a variable, we
abstract ourselves from its value, but the possible values
themselves are numbers, which are not `physical' objects
but linguistic objects formed by abstraction present
in the process of counting. This intermediate linguistic level of
numbers must become reality before we use abstraction on the next
level. Without it, i.e. by a direct abstraction from countable
things, the concept of a variable could not come into being.
In the next metasystem transition we deal with abstract algebras,
like group theory, where abstraction is done over various operations.
As before, it could not appear without the preceding
metasystem level, which is now the school algebra.
Two cybernetic systems are involved in human language and thought.
The first system is the human brain. It creates models of reality whose material body is the nerve nets, and which we therefore call
neuronal models. Neuronal models use neuronal, or intuitive,
concepts (functional elements).
The second system is language. Its functioning is linguistic activity
in society. Linguistic activity creates models of reality whose material
body consists of linguistic objects. The functional elements of this
system are logical (linguistic concepts.
The two systems are tightly interrelated. Language is an offspring,
and, in a certain sense, a continuation of the brain: using language
we create new modesl of reality, which were not imbedded in our brain
by nature. Some substructures in our brain are representations of the
states of the world. Some of the linguistic objects are representations
of those representations: we refer to them as most concrete, or low-level,
concepts. Such words as "cat", "apple", "to run" , and the concepts
they fixate, are of that kind.
But human language (like human brain) is a multilevel hierarchical system.
We create theories, where we use abstractions of higher levels,
logical concepts the machinery of which (do not forget that concepts
are functional units) requires something in addition to the brain:
some material linguistic objects. Thus while we can regard small
numbers, like two or three, as neuronal concepts because we immediately
recognize them, bigger numbers, like 137, can function only using
some external to the brain representations.
The concepts of the higher levels do not replace those of the lower levels,
as they should if the elements of the language reflected things "as
they really are", but constitute a new linguistic reality, a
superstructure over the lower levels. We cannot throw away the
concepts of the lower levels even if we wished to, because then
we would have no means to link theories to observable facts.
Predictions produced by the higher levels are formulated in terms
of the lower levels. It is a hierarchical system, where the top
cannot exist without the bottom.
We loosely call the lower-level concepts of the linguistic
pyramid concrete, and the higher-level abstract.
This is correct as long as one keeps in mind that abstraction
is not always abstraction in scope from things observable, but also,
and most importantly,
an abstractions from abstractions of the lower levels of the same
linguistic system. Pure abstraction from specific
qualities and properties of things leads ultimately, as its scope
increases, to the loss of contents, to such concepts as some
and something. Abstractness of a
concept is actually its `constructness', the
height of its position in the hierarchy, the degree to which it
needs intermediate linguistic objects to have meaning and be
used. Thus in algebra, when we say that x is a variable, we
abstract from its value, but the possible values
themselves are numbers, i.e. linguistic objects formed by abstraction
in the process of counting. This intermediate linguistic level of
numbers must become reality before we use abstraction on the next
level. Without it, i.e. by a direct abstraction from countable
things, the concept of a variable could not come into being.
When langage is used for comparatively narrow professsional purposes
there is a tendency to limit the number of terms used and to give
them more precise and constant meaning. We say that the language
is being formalized. If this process is carried through
to its logical conclusion, the language will be completely
formalized, or formal. A language is formal if
its usage relies only on the `form' of linguistic objects, and not
their intuitive meanings.
To make this definition precise, we must specify a set of perceptions
(that is abstractions) and
actions which are registered and performed in the same way by
all members of the society whom the languages serves.
We shall refere to these perceptions and actions
as universally defined. A language is formal if all the processes
involved in its usage, namely the representation function R(w),
the modelling function M(r), and (for command languages) the set of
possible actions are expressed in terms of universally defined perceptions
and actions.
We usually assume that universally defined perceptions and actions
can be relegated to the machine. The question is still open
whether this is a realistic assumption. We accept it with a qualification
that if there is a doubt about a specific abstraction or action,
it nust be excluded from the universally defined set. The a formal
language is a language usable by a properly constructed machine.
A machine of that kind becomes an objective model of reality,
independent from the human brain which created it. This makes possible
a series of consecutive metasystem transitions, where each next level
deals with a well-defined, objective reality of the previous levels.
Thus the language becomes an ultrametasystem, exhibiting the
stair-case effect (see [Tur77]) and an explosive growth in volume
and power. Just as mastering the general principle of using tools
to make better tools gives rise to consecutive metasystem transitions
and the creation of industrial system, so mastering the principle of
describing (modelling) by means of a formalized language gives rise to
the creation of the hierarchical system of formal languages on which
the modern science is based.
Classification of languages by these two parameters of abstraction anf
formalization leads to the following four types of language-related
activities [Tur77].
Art is characterized by unformalized and concrete language.
Words and language elements of other types are important only as
symbols which evoke definite complexes of mental images and
emotions. Philosophy is characterized by abstract informal thinking.
The combination of high-level abstract constructs used in
philosophy with a low degree of formalization requires great
effort by the intuition and makes philosophical language the most
difficult type of the four. Philosophy borders with art when it
uses artistic images to stimulate the intuition. It borders with
theoretical science when it develops conceptual frameworks to be
used in construction of formal scientific theories. The language
of descriptive science must be concrete and precise;
formalization of syntax by itself does not play a large part, but rather
acts as a criterion of the precision of semantics.
Proclamation of any truth as absolute because of being given
through a "revelation" is sheer self-deception.
It is natural to test the validity of this approach to knowledge,
meaning and truth in the field which does not allow imprecision
and vagueness but requires a complete formalization and inambiguity,
-- in mathematics. This is done in V.Turchin's Cybernetic foundation of
mathematics. This approach gives answers to the century
old questions about foundations of mathematics;
in particular, a new and constructive interpretation
of the full set theory is proposed there.
The statement that a certain process is infinite is not a prediction.
But it is a generator of predictions. Our definition of a prediction T!
includes a procedure, let it be denoted as P(t_i), which
is applied to the states t_i, i= 1,2,... etc. of the test T
and determines, in a finite time, whether each given
state is Success, Failure, or neither of
the two, which we shall denote as Not-end. Therefore, the statement
that the state t_i is Not-end is a prediction, namely,
the success of the procedure that runs P(t_i) and compares the result
with Not-end. Now we can define what is the meaning of the statement
that T is infinite: it is a generator which produces the following
row of predictions:
t_1 is Not-end
t_2 is Not-end
t_3 is Not-end
...
etc., infinitely
We postulate and consider it self-evident that a test is either finite
or infinite. This excludes any third, or middle, possibility,
which gave this principle the name of the law of the excluded middle.
From this we derive that a prediction may be only true or false.
We further derive the law of the excluded middle for arbitrary
statements. Consider some statement S which is a generator of predictions.
Let us run this generator and define the following refutation process.
Each time that a prediction if produced it it replaced by the symbol
True if it is true and False if it is false.
The first time the symbol False appears in the refutation process,
the process ends and succeeds. This process is either finite, or infinite.
If it is infinite, the statements S is true, otherwise it is false.
No other outcome is possible.
By proof of a statement S we mean any process which the subject
of knowledge accepts as the evidence that S is true and is ready to
use S for predictions on the basis of which to make decisions.
There are two cases of proof which can never arise any doubt because
they do not base on any assumptions: verification and
direct refutation.
When a statement cannot be directly verified or refuted, it is still
possible that we take is as true relying on our intuition.
For example, consider a test process T the stages of which can be
represented by single symbols in some language.
Let further the process T develop in such
a manner that if the current stage is represented by the symbol A, then
the next stage is also A, and the process comes to a successful end
when the current stage is a different symbol, say B. This definition
leaves us absolutely certain that T is infinite, even though this cannot
be either verified, or refuted. In logic we call some most
immediate of such statements axioms and use as a basis for
establishing the truth of other statements. In natural sciences
some of the self-evident truths serve as the very beginning of the
construction of theories.
Verification is a direct use of the definition of truth to decide if
the statement is true.
Predictions are, in principle, verifiable. You only have to initiate the
test process that the prediction is about and wait until it comes to the
final state. Thus, if a prediction is correct, there is, in principle,
a way to verify this, even though it may require such a huge time, that in
practice it is impossible.
Now consider the situation when you want to verify a prediction T!,
but the test process T is infinite.
This means that the prediction is false, but you will never be able
to verify this directly. To sum up, the following three cases are
possible when we try to verify a prediction:
As to the verififcation of general statements (generators of predictions),
it may be possible only if the number of prediction produced is finite.
In the more usual case, with an infinite number of prediction produced,
the direct verification is impossible.
...
In the cybernetic foundation of mathematics [...] we show that if
we start with the
principle that a meaningful mathematical proposition is a generator
of predictions, we come to the necessity of introducing the user of
the mathematical tools into the formalism. The tools of mathematics
do not work autonomously, like Turing machines, but rather in an interactive
mode. The user of such machines is, like Einstein's observer, a form
of "I".
We distinguish between factual statements and theories. If
the path from a statement to verifiable predictions is short and
uncontroversial, we call it factual. A theory is a statement
which can generate a wide scope of predictions, but only through
some intermediate steps, such as reasoning, computation, the use
of other statements. Thus the path from a theory to predictions
may not be unique and often becomes debatable. Between
the extreme cases of statements that are clearly facts
and those which are clearly theories there is a whole
spectrum of intermediate cases.
Top-level theories of science are not deduced from
observable facts; they are constructed by a creative act, and their
usefulness can be demonstrated only afterwards. Einstein wrote:
"Physics is a developing logical system of thinking whose
foundations cannot be obtained by extraction from past experience
according to some inductive methods, but come only by free fantasy".
The statement of the truth of a theory has essentially the
same meaning as that of a simple factual judgment: we refer to
some experience which justifies, or will justify,
the decision-making on the basis of this statement.
When this experience is in
the past we say that the truth is established.
When it is expected in the future we say it is hypothetical.
There is no difference of principle between factual
statements and theories: both are varieties of models of reality which
we use to make decisions. A fact may turn out to be an illusion,
or hallucination, or a fraud, or a misconception. On the other
side, a well-established theory can be taken for a fact. And we
should accept critically both facts and theories, and re-examine
them whenever necessary. The differences between facts
and theories are only quantitative: the length of the path
from the statement to the production of predictions.
The metasystem transition from representations to their transformations
is a step towards objectivity of knowledge.
Actions and, in particular, sensations are intimately tied to the agent,
the subject of knowledge. An object is a transformation and prediction
of actions. The very fact that prediction is possible indicates
that the transformation depends less on the subject of knowledge,
the `I', and more on the `not-I'.
This does not ensure a complete objectivity; alas, there is
no such thing. But a jump from a representations to a transformation
of representations verified by the practice of correct predictions,
is the only way we know to increase objectivity.
When we perceive a tea-pot as an object, we have a lot of cognitive actions
to factor out: we can walk around it, grasp it, rotate it in from of our
eyes etc. But often we observe things from afar and that is about all
we can do, as, fro instance, when we observe a star and still call it
an object. Well, from the viewpoint of our theory, we always associate
with an object some kind of stability, and stability exist only with
respect to action. In the case of a star, this is the stability with respect
to varying conditions of observation. We can observe `the same' star
at different times and factor out the differences in time by taking into
account the rotation of the sky around the Earth's axis. The same is
true with respect to the movement of the observer around the Earth's
surface. The more we know of astronomy and physics, the greater number
of properties of the object will we discover, such as the constancy of the
star's spectrum etc.
We also must include into the concept of cognitive actions
the more sophisticated and esoteric actions which were not
among those actions for which evolution created human brain, but
emerge as a result of the development of science.
We get involved in this kind of actions when we construct huge
accelerators of elementary particles and set up experiments to explore how
the particles interact. As an apple and other physical bodies are
invariants in the processing of input information by the brain,
so an electron and other elementary particles
are invariants of the scientific symbolic models of the world.
We can measure the charge of the electron in many different ways --
which all are various cognitive actions -- but
after making all the computations required by the theory, we still
come to the same number (within the error). The same with mass, spin, etc.
So an electron is, for us, an object, as real as an apple.
One could qualify this statement by noticing that the existence of
electrons depends on the legitimacy of our physical theory, which is not
absolute. True enough. But who are we to claim that the legitimacy of
our brain as a collection of models is absolute?
The following list of nodes, linked to their definitions and cross-references, provides a first attempt to organize the fundamental concepts in the form of a semantic network. These nodes were developed by the PCP editors in August 1992, and originally implemented by Cliff Joslyn in HyperTeX, an extension of the TeX mathematical typesetting language with elementary hypertext capacities. They were converted to HTML by Johan Bollen in March 1994.
The following clickable map represents the semantic network formed by the collection of linked concepts. Links are represented by arrows, labeled with the link type. Unlabeled links are of the "is-a" type. Roots
are shaded. Concepts with rectangles (not rounded) are clickable.
Many of the concepts referred to in these definitions are still undefined, and need to be developed later. Note that concepts for which there was no consensus on the definition have been split up into two (or more) concepts, tagged with the first letter of their author's last name. E.g. HJ-distinction is a definition of the "distinction" concept as proposed by Heylighen and Joslyn, T-distinction is the corresponding definition proposed by Turchin. Different senses of the same word have been tagged with subsequent numbers to distinguish them. This list of terms gives a first idea of the process of semantic analysis which is at the basis of PCP development.
The concept of the metasystem transition in formal systems is applied in a research program on computer program optimization through
partial and lazy evaluation methods, culminating in a Supercompiler. For more information, see the following review paper:
The aspects of distinction and connection determine two dimensions characterizing complexity. Distinction corresponds to variety, to heterogeneity, to the fact that different parts of the complex behave differently. Connection corresponds to constraint, to redundancy, to the fact that different parts are not independent, but that the knowledge of one part allows the determination of features of the other parts. Distinction leads in the limit to disorder, chaos or entropy, like in a gas, where the position of any gas molecule is completely independent of the position of the other molecules. Connection leads to order or negentropy, like in a perfect crystal, where the position of a molecule is completely determined by the positions of the neighbouring molecules to which it is bound. Complexity can only exist if both aspects are present: neither perfect disorder (which can be described statistically through the law of large numbers), nor perfect order (which can be described by traditional deterministic methods) are complex. It thus can be said to be situated in between order and disorder, or, using a recently fashionable expression, "on the edge of chaos".
The simplest way to model order is through the concept of symmetry, i.e. invariance of a pattern under a group of transformations. In symmetric patterns one part of the pattern is sufficient to reconstruct the whole. For example, in order to reconstruct a mirror-symmetric pattern, like the human face, you need to know one half and then simply add its mirror image. The larger the group of symmetry transformations, the smaller the part needed to reconstruct the whole, and the more redundant or "ordered" the pattern. For example, a crystal structure is typically invariant under a discrete group of translations and rotations. A small assembly of connected molecules will be a sufficient "seed", out of which the positions of all other molecules can be generated by applying the different transformations. Empty space is maximally symmetric or ordered: it is invariant under any possible transformation, and any part, however small, can be used to generate any other part.
It is interesting to note that maximal disorder too is characterized by symmetry, not of the actual positions of the components, but of the probabilities that a component will be found at a particular position. For example, a gas is statistically homogeneous: any position is as likely to contain a gas molecule as any other position. In actuality, the individual molecules will not be evenly spread. But if we look at averages, e.g. the centers of gravity of large assemblies of molecules, because of the law of large numbers the actual spread will again be symmetric or homogeneous. Similarly, a random process, like Brownian motion, can be defined by the fact that all possible transitions or movements are equally probable.
Complexity can then be characterized by lack of symmetry or "symmetry breaking", by the fact that no part or aspect of a complex entitity can provide sufficient information to actually or statistically predict the properties of the others parts. This again connects to the difficulty of modelling associated with complex systems.
Havel (1995) calls a system "scale-thin" if its distinguishable structure extends only over one or a few scales. For example, a perfect geometrical form, like a triangle or circle, is scale-thin: if we zoom out, the circle becomes a dot and disappears from view in the surrounding empty space; if we zoom in, the circle similarly disappears from view and only homogeneous space remains. A typical building seen from the outside has distinguishable structure on 2 or 3 scales: the building as a whole, the windows and doors, and perhaps the individual bricks. A fractal or self-similar shape, on the other hand, has infinite scale extension: however deeply we zoom in, we will always find the same recurrent structure. A fractal is invariant under a discrete group of scale transformations, and is as such orderly or symmetric on the scale dimension. The fractal is somewhat more complex than the triangle, in the same sense that a crystal is more complex than a single molecule: both consist of a multiplicity of parts or levels, but these parts are completely similar.
To find real complexity on the scale dimension, we may look at the human body: if we zoom in we encounter complex structures at least at the levels of complete organism, organs, tissues, cells, organelles, polymers, monomers, atoms, nucleons, and elementary particles. Though there may be superficial similarities between the levels, e.g. between organs and organelles, the relations and dependencies between the different levels are quite heterogeneous, characterized by both distinction and connection, and by symmetry breaking.
We may conclude that complexity increases when the variety (distinction), and dependency (connection) of parts or aspects increase, and this in several dimensions. These include at least the ordinary 3 dimensions of spatial, geometrical structure, the dimension of spatial scale, the dimension of time or dynamics, and the dimension of temporal or dynamical scale. In order to show that complexity has increased overall, it suffices to show, that - all other things being equal - variety and/or connection have increased in at least one dimension.
The process of increase of variety may be called differentiation, the process of increase in the number or strength of connections may be called integration. We will now show that evolution automatically produces differentiation and integration, and this at least along the dimensions of space, spatial scale, time and temporal scale. The complexity produced by differentiation and integration in the spatial dimension may be called "structural", in the temporal dimension "functional", in the spatial scale dimension "structural hierarchical", and in the temporal scale dimension "functional hierarchical".
It may still be objected that distinction and connection are in general not given, objective properties. Variety and constraint will depend upon what is distinguished by the observer, and in realistically complex systems determining what to distinguish is a far from trivial matter. What the observer does is picking up those distinctions which are somehow the most important, creating high-level classes of similar phenomena, and neglecting the differences which exist between the members of those classes (Heylighen, 1990). Depending on which distinctions the observer makes, he or she may see their variety and dependency (and thus the complexity of the model) to be larger or smaller, and this will also determine whether the complexity is seen to increase or decrease.
For example, when I noted that a building has distinguishable structure down to the level of bricks, I implicitly ignored the molecular, atomic and particle structure of those bricks, since it seems irrelevant to how the building is constructed or used. This is possible because the structure of the bricks is independent of the particular molecules out of which they are built: it does not really matter whether they are made out of concrete, clay, plaster or even plastic. On the other hand, in the example of the human body, the functioning of the cells critically depends on which molecular structures are present, and that is why it is much more difficult to ignore the molecular level when building a useful model of the body. In the first case, we might say that the brick is a "closed" structure: its inside components do not really influence its outside appearance or behavior (Heylighen, 1990). In the case of cells, though, there is no pronounced closure, and that makes it difficult to abstract away the inside parts.
Although there will always be a subjective element involved in the observer's choice of which aspects of a system are worth modelling, the reliability of models will critically depend on the degree of independence between the features included in the model and the ones that were not included. That degree of independence will be determined by the "objective" complexity of the system. Though we are in principle unable to build a complete model of a system, the introduction of the different dimensions discussed above helps us at least to get a better grasp of its intrinsic complexity, by reminding us to include at least distinctions on different scales and in different temporal and spatial domains.
In particular, we regard the following concepts as utterly fundamental to,
inseparable within, and inextricably interrelated in any system of thought
which can be described as "cybernetic". As (current) foundations they can
be described, but not defined in terms of other concepts. As such they are
essentially and necessarily undefined. While these three concepts form the
(current) foundation for Metasystem Transition Theory, the following subsections detail
fundamental concepts which follow directly from these.
Actions are the fundamentals of reality in Metasystem Transition Theory. Our
philosophy is process oriented, where change and evolution are emphasized
over objects, entities, and static properties. This is fundamentally in
keeping with other process philosophies \cite{WHA29} and much of cybernetic
theory \cite{?} (see section metaphysics).
We use the concept of the distinction as the fundamental nominal notion, as the generator of all separateness, differentiation, of
all categories and dimensions, indeed of all knowledge.
Of course this concept has a long and venerable history not only in general
philosophy, but particularly in Cybernetics and Systems Science. Distinctions are recognized as
fundamental by Bateson \cite{BAG72c,BAG72e}, and were developed into an
elegant (if usually misunderstood) formal language of systems by
Spencer-Brown and others \cite{GOJVAF79,SPG,VAF75} \both{I need a ref for
S-Brown}.
Distinct categories are necessary for all communication and for all
information theory, if not all mathematics. Furthermore, the distinction between discrete distinctions and continuous differences is a
perennial issue in all Cybernetics and Systems Science. More recently, Heylighen has developed a
detailed theory of causality and action in terms of distinctions
\cite{HEF89b,HEF90d} which informs a great deal of Metasystem Transition Theory.
The subject of Metasystem Transition Theory, what Metasystem Transition Theory is about, is general
philosophy from a cybernetic perspective. But Metasystem Transition Theory itself is also an object, i.e.\ a linguistic construction almost entirely in the English
language. As such, both Principia Cybernetica and Metasystem Transition Theory must be always recognized as
existing relative to that interpretive framework.
But in the same way, all constructions of the human mind, indeed all
systems, are relativized to and embedded within particular interpretive
perspectives. We call the presence of such a perspective the presence of
the subject. The involvement of an explicit subject in all aspects of
Metasystem Transition Theory draws our attention to the level-relativity of theory and
explanation, and the inside/outside distinctions such as
system/environment.
The inside and outside are complementary, irreducible perspectives.
Everything viewed from the inside (subjective) looks and is described
differently from the outside (objective). From the inside perspective the
subject appears as God, nature, or chance; from the outside perspective
(when it is available to us) the subject appears as a willing agent. In
physics, the subject is called the observer, and the result is
quantum complementarity. In Turchin's formal theory \cite{TUV87a}, the
subject is called the user of the cybernetic machine.
Evolution typically leads to greater complexity, although one must be careful how one defines complexity.
The narrow or specific interpretation of Darwinism sees evolution as the result of selection by the environment acting on a population of organisms competing for resources. The winners of the competition, those who are most fit to gain the resources necessary for survival and reproduction, will be selected, the others are eliminated. Even when abstracting from the fact that we are speaking about "organisms", this view of evolution entails two strong restriction:
More importantly this selection does not in any way presuppose the existence of an environment external to the configuration undergoing selection. It is easy enough to imagine configurations that are intrinsically stable or unstable. A cloud of gas molecules in a vacuum (i.e. an "empty" environment) will diffuse, independently of any outside forces. A crystal in the same vacuum will retain its rigid crystalline structure. The first configuration (the cloud) is eliminated, the second one maintains. The stability of the structure, functioning as a selection criterion, is purely internal to the configuration: no outsides forces or pressures are necessary to explain them.
In cases like these, the selection is inherent in the configuration itself, and an asymmetric transition from varying to stable may be called "self-organization". In the present view, "natural selection" encompasses both external, Darwinian selection, and internal, "self-organizing" selection.
See also: Servers on Evolutionary Theory
Self-organization is a basically a process of evolution where the effect of the environment is minimal, i.e. where the development of new, complex structures takes place primarily in and through the system itself. As argued in the section on evolutionary theory, self-organization can be understood on the basis of the same variation and natural selection processes as other, environmentally driven processes of evolution. Self-organization is normally triggered by internal variation processes, which are usually called "fluctuations" or "noise". The fact that these processes produce a selective retained ordered configuration has been called the "order from noise" principle by Heinz von Foerster, and the "order through fluctuations" mechanism by Ilya Prigogine. Both are special cases of what I have proposed to call the principle of selective variety.
The increase in organization can be measured more objective as a decrease of statistical entropy (see the Principle of Asymmetric Transitions). This is again equivalent to an increase in redundancy, information or constraint: after the self-organization process there is less ambiguity about which state the system is in. A self-organizing system which also decreases its thermodynamical entropy must necessarily (because of the second law of thermodynamics) export ("dissipate") such entropy to its surroundings, as noted by von Foerster and Prigogine. Prigogine called systems which continuously export entropy in order to maintain their organization dissipative structures.
Self-organization is usually associated with more complex, non-linear phenomena, rather than with the relatively simple processes of structure maintenance of diffusion. All the intricacies (limit cycles, chaos, sensitivity to initial conditions, dissipative structuration, ...) associated with non-linearity can simply be understood through the interplay of positive and negative feedback cycles: some variations tend to reinforce themselves (see Autocatalytic Growth), others tend to reduce themselves. Both types of feedback fuel natural selection: positive feedback because it increases the number of configurations (up to the point where resources become insufficient), negative feedback because it stabilizes configurations. Either of them provides the configuration with a selective advantage over competing configurations. The interaction between them (variations can be reinforced in some directions while being reduced in others) may create intricate and unpredictable patterns, which can develop very quickly until they reach a stable configuration (attractor).
See also:
News- May/June 1997
http://www.cpm.mmu.ac.uk/jom-emit/). The website is getting more and more popular, and the associated mailing list for memetics discussions has become very active, with 500 messages in its first 5 weeks (see the archive at http://www.cpm.mmu.ac.uk/~majordom/memetics/). However, there are not as yet many new proposals for papers, and authors are still solicited to submit manuscripts.News- Sept/Oct 1997
http://www.eur.nl/fsw/soc/happiness.html) Veenhoven himself was enthusiastic to join the group and to collaborate on a joint research proposal. It was agreed to start preparing an edited book, in which different contributors would discuss the different aspects and mechanisms of global progress, such as economic growth, increase in life expectancy, raise in education level and IQ, and improvement in the overall the quality of life. The book is planned to be ready by the year the 2000. Veenhoven suggested the title "The Optimistic Manifesto", but this is of course still open for discussion.News- Nov/Dec 1997
http://www.c3.lanl.gov/~joslyn/ISAS98/) chaired by PCP editor Cliff Joslyn and PCP associate Luis Rocha. Though the meetings concern different topics, they fall in about the same period, respectively August and September 1998. The first is organized by the "Journal of Memetics" associated with PCP and is part of the 15th Int. Congress on Cybernetics, the second is part of the 1998 Conference on Intelligent Systems and Semiotics.http://www.santafe.edu/~bonabeau/), edited by our friend Eric Bonabeau from the Santa Fe Institute. The general subject is close to PCP themes, and PCP editor Cliff Joslyn is member of its editorial board.News- Jan/Feb 1998
http://www.unine.ch/CIESYS/ECOLE.html), although this is independent of PCP.News- March/April 1998
http://www.c3.lanl.gov/~joslyn/pcp/workshop98.html). This ties in with our work on self-organizing networks and the global brain.http://www.lehigh.edu/~mhb0/mhb0.htmlNews - May/June 1998
Our plans for the annual board meeting of PCP in Santa Fe, New Mexico, have become more concrete. Johan Bollen, Alex Riegler, Cliff Joslyn and Francis Heylighen will meet during the period August 1 to 20, and will be joined by Valentin Turchin from August 9. The accompanying workshop on "Emergent Semantic and Computational Processes in Distributed Information Systems" (see http://www.c3.lanl.gov/~joslyn/pcp/workshop98.html) on August 10-11 is now taking concrete shape, with most abstracts available on the web. This workshop wil hopefully be the start for a fruitful collaboration between PCP and the "Symbiotic Intelligence Project" (http://ishi.lanl.gov/symintel.html), which groups researchers from Los Alamos National Laboratory and Santa Fe Institute. The subject would be the application of self-organizing systems to support collective intelligence on the web.http://www.cpm.mmu.ac.uk/jom-emit/1997/vol1/gabora_l.htmlhttp://HyperNews.ngdc.noaa.gov/HyperNews/get/ecosci/1.html News - July/August 1998
BOARD MEETING IN NEW MEXICOhttp://www.c3.lanl.gov/~joslyn/pcp/workshop98.html). Afterwards, workshop
proceedings will be published, most likely as a LANL internal report at
first, and as a book or special issue of a journal in a second stage. This
second stage is likely to propose a selection of the most relevant papers,
rewritten to take into account the other contributions, together with some
newly invited papers from people who did not attend the workshop but who
are experts in the domain.http://ishi.lanl.gov/symintel.html), John Casti from SFI, who was
interested to publish a report of the workshop in the journal "Complexity"
which he edits, Eric Bonabeau, another SFI resident and editor of "Complex
Systems", who is a world authority on the collective intelligence exhibited
by insect societies, and Liane Gabora, a memetics researcher affiliated to
UCLA.First public introduction of the Principia Cybernetica Project
Author: Cliff Joslyn, and Valentin Turchin,
Updated: 23 Dec 89
Filename: FPUBINT.html
Date: Sat, 23 Dec 89 12:41:22 EDT
Sender: Cybernetics and Systems
Progress Report: 5 years of PCP
Author: F. Heylighen, C. Joslyn,
Updated: Oct 11, 1994
Filename: PROGREP.html
PCP was publically introduced in December 1989 with a first general proposal, containing a list of goals. Since these objectives were formulated rather explicitly, point by point, it is easy to now check in how far they have become reality. Although these goals sounded very ambitious at the moment, the funny thing is that most of them have effectively been realized. The following is a partial list of desiderata for the "Principia Cybernetica" project:
YES. The system of philosophy is there (albeit far from finished), partially implemented over the WWW server, and its developers have been working collaboratively in spite of large geographical obstacles (the Atlantic Ocean among other things).
2. To allow these researchers different levels of access to the system according to their role in the project development
YES. The present WWW server allows editors to read and edit all material via passwords, the different contributors to read most material, and to make annotations. Soon they will be able to edit their own annotation (but not other people's)
3. To produce a system of philosophy that can develop dynamically over time, with continuing refinement and expansion
YES. The quasi-hierarchical hypertext structure of linked nodes makes it easy to add or refine concepts and principles, while maintaining a stable core.
4. For the system of philosophy to fully reflect and incorporate the semantic relations inherent among the terms being explicated
Mostly NO. Some semantic relations have been made explicit in a system of typed links for certain nodes, but this is basically an unfinished experiment.
5. To allow the explication of terms and senses of terms, and to unify and synthesize notations and terminology among researchers in different disciplines
Mostly NO. There is some explication of terms and senses of terms (e.g. in the Glossary), but it is far from systematical, and we certainly haven't as yet achieved any terminological unification.
6. To support the process of argument and dialog among experts toward the end of consensus at the level of the meanings of words and the relations among those meanings
MAYBE. PRNCYB-L and the annotations on the server, as well as more traditional meetings and publications can certainly be said to "support" argument and dialog, but the end of consensus is still quite far away.
7. To support the publication of intermediate and final stages of parts or the whole of the philosophical system
YES. Several papers have already been published, and the hierarchical organization of the conceptual network should make it relatively easy to take out parts or the whole and publish them as a book, paper or report.
8. To support bibliographical and historical reference
YES. In a hypertext system this is almost trivial. Just make a link to a node with a historical review or a list of publications. The actual lists of publications and historical overviews are virtually non-existent though.
9. To support mathematical notation and the easy movement among natural language, formal language, and mathematics
Mostly NO. A shortcoming of the HTML markup language for WWW is that as yet it does not provide easy ways to express mathematical notations, though that should be facilated in the future (e.g. by automatic HTML<->TEX conversions). The "easy movement" is rather vague, so it is difficult to conclude in how far it has been achieved.
10. To allow researchers to develop or read the philosophical system in various orders and in various degrees of depth or specificity
YES. The Principia Cybernetica Web can be read in many different orders, and readers can go in depth, or remain more on the surface while still getting a basic picture. More work needs to be done to fill in all the different levels, though.
11. To allow access to the system for both participants who wish to author and users who wish to read, browse, or study
YES. WWW now allows both reading of text and entering of new text through annotation.
12. To support the publication of various special-purpose documents, including dictionaries, encyclopedias, texts on a subject, reference pages, essays, dialogs on a subject, or "streams of consciuosness"
MAYBE. Several of these types of texts have been published, and as stated earlier it should be easy to take out parts of the Web, but it is not clear in how far the generation of these special purpose documents is really "supported".
13. To allow the representation and utilization of knowledge in both its breadth and its depth.
Probably YES. Representation in breadth and depth is certainly supported, but the rest is rather vague. It sounds well but it is not clear in how far PCP knowledge is being "utilized". If the number of people consulting the Web is a measure, it is certainly not being ignored, though one can doubt whether much is retained by the readers.
The Cybernetic Manifesto
Author: V. Turchin, C. Joslyn,
Updated: Oct 1989
Filename: MANIFESTO.html
1.Philosophy
2.Knowledge
3.Freedom, will, control
4.God
5.Metasystem transition
6.Evolution
7. Human intelligence
8.Social integration
9.The era of Reason
10.Global integration
11.Human super-beings
12.Ultimate human values
13.Decline of metaphysical immortality
14.Creative immortality
15.Cybernetic immortality
16.Evolution and immortality
17.Evolution of the human person
18. How integration may occur
19.Integration on the Cosmic scene
20.Current problems
21.Integration and freedom
Reactions, discussions, comments
Author: F. Heylighen, V. Turchin,
Updated: Jul 19, 1994
Filename: REACT.html
The following is a list of reactions and criticisms in different places of the Principia Cybernetica Project and its Web server. See also: User Annotations.
Criticisms of Principia Cybernetica
Author: F. Heylighen & C. Joslyn
Updated: Aug 1993
Filename: CRITIC.html
Turchin an Joslyn originally announced Principia Cybernetica by posting a first general proposal, and "The Cybernetic Manifesto on the CYBSYS-L electronic mailing list in the autumn of 1989 (see the Project history). This led to a a sometimes very heated debate. The most outspoken critic was Joseph Goguen, who interpreted the use of concepts like "control", "hierarchy" and "integration" as signs of a dangerous, totalitarian ideology. Joslyn and Turchin reacted by stressing the essential role human freedom plays in the philosophy, and by remarking that terms like control and hierarchy should be understood primarily in their abstract, technical sense. In fact, the metasystem transition, where a new control level emerges, should be seen as an increase, rather than a decrease, of the freedom of the system. This criticism led to a deeper understanding of the necessity for careful articulation of the ideas behind Principia Cybernetica, in the hope of avoiding misinterpretation.Principia Cybernetica Web and the "Best of the Web" awards
Author: F. Heylighen,
Updated: Jul 19, 1994
Filename: BESWEB.html
Principia Cybernetica Web has participated in the 1994 "Best of the Web" awards, an international competition for the best services on the World-Wide Web. PCP Web was originally nominated for the category "Document Design" with the following quotation:
Principia Cybernetica Web
Document Design" category. The award in this category went to "Travels with Samantha", a narrative with lots of splendid color photographs and an interesting story, but nothing much in the area of hypertext design.
Principia Cybernetica in "Wired" magazine
Author: Wired
Updated: Jul 19, 1994
Filename: REVWIR.html
The following is a quote from WIRED, a popular magazine devoted to cyberspace.
(WIRED: San Francisco, Wired Ventures ltd., nr. 2.08, August 1994, p. 119)
When Science Meets Net.Society.
The Principia Cybernetica Project is an attempt to unify systems theory and
cybernetics, using the tools and methods of cybernetics itself. Managed by
leading researchers from the City University of New York, NASA, and the
Free University of Brussels, Principia Cybernetica is amassing an awesome
and ever-growing info-tube of information on the underlying meme-technology
of the Matrix: self-organizing systems, cybernetics, human-computer
interaction, knowledge structures, cognitive science, artificial
intelligence, philosophy, and evolution, to name a few. No ivory towers
here, simply practical information on web-weaving and Internet use
commingled with academic papers and cyberculture rants, such as Ronfeldt's
Cyberocracy.
References to Principia Cybernetica in different servers
Author: F. Heylighen,
Updated: Jul 23, 1998
Filename: REFSPCP.html
The Principia Cybernetica Web is being linked to by more and more other Web pages. You can get a complete list of the about 5000 sites linking to PCP Web from the AltaVista catalog. Many of them only mention the name of the project as anchor, or include some of our own characterizations of the project, but some of them also add a personal evaluation. (see also the review in Wired magazine, and the nomination for the Best of the Web Awards) find further references to PCP yourself via the Altavista search engine.Personal appreciation
"Principia Cybernetica Project. Philosophy on the Net. As only could be done on the Net. This is complex but amazing." (
Cool links)Evolution Resources on the Internet)Virtual Reality Research)Recommended Internet Resources)http://www.honors.indiana.edu/docs/interest.html)Web Sites With Information on
Systems Science Topics)
Principia Cybernetica" (Onar Aam's Related Servers page)Expanding Your
Consciousness )
Media lab).
"an excellent site" (Wiener: ideas)
Quality related Information Sources)
Frontier organizations on the Web)
Guide to Autopoiesis related Internet Resources)
Psychology and Psychotherapy sources)
Joë de Rosnay's list of Web Future Sites)
Teor*ias Generales de Avanzada)TRAP CITY: A Serial Story)
Reviews by web services
Global Network Navigator)
Netscape's "What's Cool" list)
Net Appeal: 8 [out of 10], Depth of Coverage: 8, Ease of Exploration: 8
Audience: Philosophers, Evolutionists, System Theorists
Description: The Principia Cybernetica Web is the home of a project that promotes the computer-supported collaborative development of an evolutionary-systemic philosophy. This project tackles philosophical questions with the help of cybernetic theories and technologies. Visitors to the site will find an overview of the plan and details of its metasystem transition theory, among others."
(Magellan's review of the PCP site)
The Principia Cybernetica Project is an in-depth look at the whole of philosophical thought, and it's not for
armchair thinkers. Using a system of "nodes," it attempts to fill in the whole of human philosophical
thought, from ethics to physics to evolutionary theory. In its complete form, the authors maintain it will
give you the answer to basic questions like "Who am I? Why am I here?" It's quite involving, though
occasionally we'd be happy with the answer to "What the heck does this mean?" on some of these pages. " (Point's review of the PCP site)
"A platinum site: Overall Rating: 5 stars (out of 5), content: 5 stars, presentation: 4 stars, personality: 4 stars
The Principia Cybernetica Project brings together a number
of scholars from around the globe to tackle age-old
philosophical problems with the aid of modern cybernetic
theories and technologies. If cyberphilosophy is your forte,
you can delve into subtopics that include ethics,
metaphysics, ontology, and many other disciplines identified
by long words. Even people with less arcane interests will
find the Web Dictionary of Cybernetics and Systems useful." (NETGUIDE'S BEST OF THE WEB, details on PCP site)
Congratulations! Your page:
http://cleamc11.vub.ac.be/
has been selected to receive a Links2Go Key Resource award in the
Philosophy topic. The Links2Go Key Resource award is both exclusive and objective. Fewer
than one page in one thousand will ever be selected for
inclusion. Further, unlike most awards that rely on the subjective
opinion of "experts," many of whom have only looked at tens or
hundreds of thousands of pages in bestowing their awards, the Links2Go
Key Resource award is completely objective and is based on an analysis
of millions of web pages. During the course of our analysis, we
identify which links are most representative of each of the thousands
of topics in Links2Go, based on how actual page authors, like
yourself, index and organize links on their pages.
Context of Principia Cybernetica
Author: C. Joslyn, F. Heylighen,
Updated: Aug 1993
Filename: CONTEXT.html
PCP as a collaborative attempt to integrate and found existing knowledge has predecessors in general intellectual history (Talmud, Adler), as well as in the history of systems science and cybernetics. In particular different similar attempts to build compendia or "encyclopedia-like" works can be mentioned, such as Krippendorf's Dictionary of Cybernetics, Singh's Systems and Control Encyclopedia, Charles François' Dictionary of Systems and Cybernetics, the work of Troncale and Snow in the context of the International Society for Systems Science, and the Glossary on Cybernetics and Systems Theory developed for the American Society for Cybernetics. Whitehead and Russell's Principia Mathematica, and
the Bourbaki group's cooperative work on the set-theoretic foundations of mathematicsPrincipia Cybernetica-related research in systems and cybernetics
Updated: Aug 1993
Filename: PCPCYBS.html
[Node to be completed]Metasystem Transition Theory
Author: C. Joslyn, F. Heylighen, V. Turchin,
Updated: Jul 7, 1997
Filename: MSTT.html
Metasystem Transition Theory (MSTT) is the name we have given our particular
cybernetic philosophy. Its most salient concept is, of course, the Metasystem Transition (MST), the evolutionary process by which higher levels of complexity and control are generated. But it also includes our views on philosophical problems, and makes predictions about the possible future
of mankind and life. Our goal is to create, on the basis of cybernetic concepts, an
integrated philosophical system, or "world
view", proposing answers to the most fundamental questions about
the world, ourselves, and our ultimate values.Background of the theory
The concept of the metasystem transition was
introduced in Turchin's book The
Phenomenon of Science, which was followed by
Inertia of Fear and the Scientific Worldview.
The basic tenets
of MSTT were formulated by Turchin and Joslyn in "The
Cybernetic Manifesto". As Heylighen joined the Editorial Board, the work on MSTT
intensified, and the Principia Cybernetica
Web was created. A major collection of papers on MSTT by the three
editors and invited authors was published in a special issue of the journal
World Futures entitled "The Quantum of Evolution". MSTT is also being applied to computer science and the foundations of mathematics by Turchin and his colleagues.
The bibliography of PCP includes most publications on MSTT.Methodology for the Development of MSTT
Author: F. Heylighen, C. Joslyn,
Updated: Oct 6, 1997
Filename: METHODOL.html
The methodology used by the Principia Cybernetica Project to build a complete philosophical system is based on a "bootstrapping" principle: the form through which the knowledge is expressed affects its content, and vice versa. Thus, our theories about the evolutionary development of systems are applied to the development of the theory itself, while the structuring of concepts in the form of an evolving semantic network suggests new theoretical concepts (see form and content). A first requirement to develop such concepts is semantic analysis and consensus building about the meaning of terms. This meaning is as much as possible expressed formally through the links between nodes, resulting in a semantic network structure for the web. Multiple Beginnings, Meta-Foundationalism
Author: C. Joslyn,
Updated: Aug 1993
Filename: MULTBEG.html
The emphasis that Principia Cybernetica places on consensus about fundamental concepts and
principles can be criticized as risking the dangers of formalism and
foundationalism, of adopting a deductive strategy in which cybernetic
theory is linearly derived or proved from axioms. The risks of such
approaches are obvious: either the development of an ossified, static
philosophy which cannot adapt to new information; or an endless, futile
search for the ultimate, jointly necessary and sufficient axiom set from
which "truth" could be derived. Multiple axiomatization sets, a metaphor for metafoundationalism
Author: C. Joslyn, F. Heylighen,
Updated: Sep 1993
Filename: MULTAXIO.html
A simple metaphor for our understanding of metafoundationalism can be found in mathematics. Mathematical systems are defined by a set of axioms, from which theorems are deduced. A mathematical theory might be defined as the set of all propositions that are true under the given set of axioms (theorems). For example, a theory of addition would contain propositions like "1 + 2 = 3", "2 + 5 = 3 + 4", and axioms like "a + b = b + a", "a + 0 = a", etc. Now, it is a well-known fact that in general the same theory can be generated by multiple sets of axioms. For example, the Boolean logic of propositions has many different axiomatizations which are formally equivalent (producing the same theorems), though one may be preferred to the other on the grounds of simplicity, esthetic appeal or explicitness. Physical Constructivism
Author: F. Heylighen, C. Joslyn,
Updated: Jan 1992
Filename: PHYSCONS.html
The philosophy of the Principia Cybernetica Project also finds its basis in what we call
"physical constructivism". While constructivism is traditionally known in
its mathematical context, including the denial of reductio ad
absurdum proofs, the existence of actually infinite objects, and the law
of the excluded middle{As described more elsewhere , cite{TUV87a} is a
constructive philosophy of mathematics from the perspective of Principia Cybernetica.}
Cyberneticians especially have championed a broader interpretation
that extends to psychology and the general philosophy of science. Metaphysics
Author: F. Heylighen, C. Joslyn, V. Turchin,
Updated: Sep 10, 1997
Filename: METAPHYS.html
Philosophies traditionally start with a metaphysics: a theory of the essence of things, of the fundamental principles that organize the universe. Metaphysics is supposed to answer the question "What is the nature
of reality?". But we cannot answer this
question without first understanding what is the meaning of metaphysics, if any, and in what respect metaphysics differs from science, which tries to answer similar questions but through more concrete methods.
Metaphysics is traditionally subdivided in ontology, the theory of being in itself, and cosmology, the theory describing the origin and structure of the universe.
Metaphysics
Author: F. Heylighen, C. Joslyn, V. Turchin,
Updated: Sep 10, 1997
Filename: METAPHYS.html
Philosophies traditionally start with a metaphysics: a theory of the essence of things, of the fundamental principles that organize the universe. Metaphysics is supposed to answer the question "What is the nature
of reality?". But we cannot answer this
question without first understanding what is the meaning of metaphysics, if any, and in what respect metaphysics differs from science, which tries to answer similar questions but through more concrete methods.
Metaphysics is traditionally subdivided in ontology, the theory of being in itself, and cosmology, the theory describing the origin and structure of the universe.
The meaning of metaphysics
Author: V. Turchin,
Updated: Sep 1991
Filename: MEANMET.html
A metalanguage is still a language, and a metatheory a
theory. Metamathematics is a branch of mathematics.
Is metaphysics a branch of physics?Knowledge and will
Author: C. Joslyn, V. Turchin,
Updated: Aug 1993
Filename: ^KNOWILL.html
[Node to be completed]From Kant to Schopenhauer
Author: V. Turchin,
Updated: Sep 29, 1997
Filename: KASCHO.html
It was noticed by the ancient Greeks already, that
sensation is the main, and maybe the only, source of our knowledge.
In the new time, Berkley and Hume stressed this in a very strong
manner: things are our sensations.
But rationalists still believed that some crucial ideas are inborn
and have nothing to do with the imperfection of our sense organs.Action
Author: V. Turchin,
Updated: Oct 6, 1997
Filename: ACTION.html
Am Anfang war die Tat
(In the beginning there was the deed)
Goethe.
Schopenhauer's formula
for all that exists is:
the world = will + representation
Will is manifested in action. Will and action are inseparable.
We understand will as the quality that allows
to choose between the (possible) options and act.
Action and will are two faces of essentially the same phenomenon,
and in our philosophy action is its perceivable part.
We rewrite Schopenhauer's formula as follows:
the perceivable world = action + representation
Of these two parts, action has the ontological primacy.
Representation is, in the last analysis, a kind of action --
interaction of the subject and the object of knowledge.
Different subjects may have different representations of the same action.
Only action as such has a definite reality: if it took place, it did.
If did not, it did not.Agent
Author: V. Turchin,
Updated: Oct 6, 1997
Filename: AGENT.html
An agent is a representation of an action. One action may not have
more than one agent, but a single agent may cause more than one action.
The necessity of this representation is seen when we describe
a human being and want to distingush between the human's body and
and the way (s)he acts. Generally, the concept of agent takes on the
cybernetic description of some part of reality, and leaves
physical (as well as chemical and bioligical) description to physics
(chemistry, biology).Event
Author: V. Turchin,
Updated: Sep 1991
Filename: EVENT.html
[Node to be completed]Emergence
Author: V. Turchin,
Updated: Sep 1991
Filename: EMERGE.html
[Node to be completed]Domain
Author: V. Turchin,
Updated: Sep 1991
Filename: DOMAIN.html
[Node to be completed]Distinction
Author: F. Heylighen,
Updated: Nov 25, 1997
Filename: DISTINCT.html
The simplest form or structure we can imagine is a distinction. A distinction can be defined as the process (or its result) of discriminating between a class of phenomena and the complement of that class (i.e. all the phenomena which do not fit into the class). As such, a distinction structures the universe of all experienced phenomena in two parts. Such a part which is distinguished from its complement or background can be called an indication (Spencer-Brown, 1969). If more than one distinction is applied the structure becomes more complex, and the number of potential indications increases, depending on the number of distinctions and the way they are connected.
The operations of distinction, and assimilation of phenomena necessarily go together. If a cognitive system would make no distinctions, only assimilations, it would be unable to perceive different phenomena, it would react to all situations in a uniform way ; hence, it would be unable to adapt to a changing environment. On the other hand, a system which would make no assimilations, only distinctions, would be unable to anticipate; hence it would also be unable to adapt.
Formal Formulations: an extensive website on distinction logics
Laws of Form website
From The Laws of Form.
Miller: Laws of Form
Forth meets the Laws of Form
Boundary Math
Logic of Distinctions. A Protologic for a Theory of Society (book summary)
Freedom
Author: V. Turchin,
Updated: Sep 1991
Filename: FREEDOM.html
[Node to be completed]God
Author: Paul Harrison, F. Heylighen, V. Turchin,
Updated: Nov 5, 1997
Filename: GOD.html Synopsys: Arguments for and against the Existence of God
Author: Paul Harrison
Updated: Apr 3, 1997
Filename: GODEXIST.html
The polytheistic conceptions of God were criticized and derided by
the monotheistic religions. Since the Enlightenment, monotheistic
concepts have also come under criticism from atheism and pantheism.Arguments for the Existence of God
Philosophers have tried to provide rational proofs of God's
existence that go beyond dogmatic assertion or appeal to ancient
scripture. The major proofs, with their corresponding objections, are
as follows:
Objection: You cannot define or imagine a thing into
existence.
Objections: If you allow one thing to exist without cause, you
contradict your own premise. And if you do, there is no reason why
the universe should not be the one thing that exists or originates
without cause.
Objection: The principles of self-organization and evolution
provide complete explanations for apparent design.
Objections: The odds against all possible universes are
equally astronomical, yet one of them must be the actual universe.
Moreover, if there are very many universes, then some of these will
contain the possibility of life. Even if valid, the anthropic
cosmological principle guarantees only that stars and planets and
life will emerge - not intelligent life. In its weak form, the
anthropic cosmological principle merely states that if we are here to
observe the universe, it follows that the universe must have
properties that permit intelligent life to emerge.
Objections: We cannot assume that everything imagined in
mental experiences (which include dreams, hallucinations etc)
actually exists. Such experiences cannot be repeated, tested or
publicly verified. Mystical and other personal experiences can be
explained by other causes.
Objections: The usefulness of a belief does not prove its
truth. In any case, many societies have thrived without these
beliefs, while crime has thrived in theistic societies believing in
heaven and hell.General objection against all the rational proofs for God:
Each of the above arguments is independent of the others and
cannot logically be used to reinforce the others.
The cause argument - even if it were valid - would prove only a first
cause. It would tell us nothing about the nature of that cause, nor
whether the cause was mental or physical. It would not prove that the
first cause was the personal, judging, forgiving God of Judaism,
Christianity, or Islam. It would not prove the existence of a
designer or of a perfect being. Equally, the design argument would
prove only a designer, the ontological argument would prove only the
existence of a perfect being, and so on. None of these arguments
individually can prove that the cause, designer or perfect being were
one and the same - they could be three different beings.
Arguments against the existence of God
Pantheism
Author: Paul Harrison
Updated: Mar 28, 1997
Filename: PANTHEISM.html Synopsys: or
naturalistic pantheism believes that the Universe either originated itself
out of nothing, or has existed forever.
Modern scientific pantheism is materialistic. It believes that design in
the universe can be fully accounted for by principles of
evolution and self-organization. It does not
believe in separate spirits or survival of the soul after death. Pantheists
concerned about personal immortality seek it in realistic ways - through
children, deeds, works, and the memories of the living.Modern pagans frequently claim to be
pantheists. Those who are concerned with logical consistency regard their
various deities as symbolic rather than real. Those who are not so concerned
combine
pantheism with literal polytheism and belief in magic, reincarnation and other
supernatural phenomena.Hegel, and in more
modern times by A. N. Whitehead and Teilhard de Chardin (see also: process metaphysics). Another variant is
the idea that humans are in some way the mind of the universe (see also: the global brain). Our evolution -
indeed our active help - is seen as helping the universe to attain its full
potential (cf. Creative Immortality).Atheism
Author: F. Heylighen,
Updated: Aug 8, 1994
Filename: ATHEISM.html Synopsys: Occam's Razor as justification of atheism)
alt.atheism FAQ Web
Basic Concepts of Science
Author: V. Turchin,
Updated: Sep 1991
Filename: SCICONC.html
[Node to be completed]State of the world
Author: V. Turchin,
Updated: Sep 1991
Filename: STATE.html
[Node to be completed]Space
Author: V. Turchin,
Updated: Sep 1991
Filename: SPACE.html
[Node to be completed]Time
Author: V. Turchin,
Updated: Sep 1991
Filename: TIME.html
[Node to be completed]Historic record
Author: V. Turchin,
Updated: Sep 1991
Filename: HISTOREC.html
[Node to be completed]Objectification
Author: V. Turchin,
Updated: Sep 1991
Filename: OBJFIC.html
[Node to be completed]Causality
Author: V. Turchin,
Updated: Sep 1991
Filename: CAUSE.html
[Node to be completed]
True True
---------------
^ ^
| |
S | | E
| |
| C |
----------------
The second prediction:
True False
---------------
^ ^
| |
S | | E
| |
| do nothing |
----------------
In words: if a situation recognized by abstraction S holds, and I do
action C, then a situation characterized by abstraction E takes place.
But if in the same situation I do nothing, then E does not occur.
This precisely matches our intuitive understanding of causality.
True True
---------------
^ ^
| |
S+obs(C) | | E
| |
| do nothing |
----------------
The second prediction:
True False
---------------
^ ^
| |
S | | E
| |
| do nothing |
----------------
However, this is not a correct expression of causality. This is only
an observation of time sequence, even though in two versions. It could
be that there exists a real cause C' which first causes action C,
and then situation E. For example, I can, on some days, have scrambled
eggs for breakfast. On such days I break two eggs and fry the content
in a frying-pan. An external observer will see that when I break eggs,
I always fry them; when I do not break eggs (say, because of having
a cheese sandwich for breakfast), I do not fry them. This is not to say
that the above two predictions cannot be part of our knowledge.
They can. They constitute a useful model of my uninterrupted
breakfest, which specifies the order of my actions. But it would
be an error to conclude that breaking eggs is the cause of frying them.
True True
---------------
^ ^
| |
S | | E
| |
| allow C |
----------------
The second prediction:
This is how sombody's else action is reduced to mine. Allowing an action
to happen is easy: just do nothing. But what about the feasibility of
prevention? When I say that rotation of the Earth is the cause of
alternation of day and night, the meaning of it is, according to our
scheme, that if I stop the rotation of the Earth, the effect
of alternation will disappear. But this clearly is impossible assumption.
And it would not help to qualify this assumption as occuring in my
imagination. Pictures in our imagination are constructed from pieces of
our real experience. Stopping the Earth was not in our experience; it is
unimaginable.Object
Author: V. Turchin,
Updated: Sep 29, 1997
Filename: OBJECT.html
An object is a representation of a relation between actions.
In the simplest case it is a subset of A1x A2, where A1
and A2 are some sets of actions. Such an object is a set
of ordered pairs a1, a2> with ai \in Ai.
Such a pair tells that if action a1 takes place, then
it is followed by a2.
A more precise definition of an object can be achieved through relations
including more variables, including those which stand for other
representations: we allow here metasystem transitions which,
in the last analysis take us back to actions.
The most important part here is the third; the first two can be subsumed
by it. We define an object b as a family of functions fa:Process
Author: V. Turchin,
Updated: Sep 1991
Filename: PROCESS.html
A process is a conceptual scheme (an abstraction of the second level). The concepts we call processes are characterized
by the following features:
Number
Author: V. Turchin,
Updated: Sep 1991
Filename: NUMBER.html
[Node to be completed]Infinity
Author: V. Turchin,
Updated: Sep 1991
Filename: INFINITY.html
[Node to be completed]Continuous vs. discrete
Author: V. Turchin,
Updated: Sep 1991
Filename: CONTIN.html
[Node to be completed]Observation
Author: V. Turchin,
Updated: Sep 1991
Filename: OBSERV.html
[Node to be completed]System
Author: C. Joslyn, V. Turchin,
Updated: Aug 1993
Filename: ^SYSTEM.html
[Node to be completed]Epistemology
Author: F. Heylighen, C. Joslyn, V. Turchin,
Updated: Jun 29, 1995
Filename: EPISTEM.html
What is knowledge? This is the basic question defining the domain of epistemology. Knowledge
Author: V. Turchin,
Updated: Sep 1991
Filename: KNOW.html
[Node to be completed] Model
Author: C. Joslyn, V. Turchin,
Updated: Aug 1993
Filename: MODEL.html
Metasystem Transition Theory understands knowledge as the existence in a cybernetic
system of a model of some part of reality. The most immediate
kind of a model is a metasystem which implements a homomorphic relation
between states of two subsystems, a modeled system and a modeling
system [ HeH94
RoR85a ].
_________________________________________|||
S|
| _|_ _ _ _ _ _ _ _ | |
| W |
|| || w2 = L(w1) || ||
| | w1 ______- w2 | |
|| _|_|_ _ _ _ _ _|_ | ||
| | | |
m1|= E(w1) || || m2 = E(w2) |
|| _|_|_ _ _ _ _ _|_ | ||
| |? |? |
| | m1 ______-m2 | |
|| || m2 = R(m1) || ||
|| _|_ _ _ _ _ _ _M_ | ||
|________________________________________|
Figure: The Modeling Relation
Homomorphism
Author: Turchin,
Updated: Sep 29, 1997
Filename: HOMOMORP.html
The mathematical definition of group homomorphism is as follows.
Let G1 and G2 be groups with the operations O1 and O2,
respectively. A mapping M from G1 to G2 is a homomorphism
if M(O1(x,y)) = O2(M(x),M(y)) for all x,y \in G1.Prediction
Author: V. Turchin,
Updated: Sep 1991
Filename: PREDICT.html
[Node to be completed]Problem-solving
Author: F. Heylighen
Updated: May 19, 1998
Filename: PROBSOLV.html Synopsys:
.
"Meta-Cognitive" Reasoning
Author: F. Heylighen, C. Joslyn,
Updated: Aug 1993
Filename: METACOGN.html
When we introduce concepts or models, their definition often requires more
than the simple description of the world in terms of these concepts. It
further requires an analysis of how we use a concept, how we happened to
introduce it, how it could possibly be modified in order be more adequate,
etc. Our reasoning in this process is metacognitive, a reasoning
not about "the world as it is", but about the relation of our own knowledge
to the world and to the goals we pursue. Principles of Reasoning with Uncertainty
Author: C. Joslyn,
Updated: Nov 27, 1995
Filename: MINIMAX.html
Cybernetics and Systems Science have produced some very important
principles of information and uncertainty cite{CHR80a,KLG90b}. It should
be emphasized that these principles were developed in the context of
specific theories which represent information and uncertainty using a
particular mathematical formalism of variety,
usually probability and thereby stochastic information theory. Instead, we
will here describe these principles using the general concept of variety.
Uncertainty Maximization
In inductive reasoning, use all, but no more than, the available
information.
Uncertainty Minimization
In deductive reasoning, lose as little information as
possible.
Uncertainty Invariance
When transforming a system, make the amount of information in the
resulting system as close as possible to that in the original. The Principle of Incomplete Knowledge
Author: F. Heylighen,
Updated: Aug 1993
Filename: ^INCOMKNO.html
The model embodied in a control system is necessarily incompleteEvolutionary Approach to Epistemology
Author: F. Heylighen,
Updated: Jul 14, 1995
Filename: EVOLEPIST.html
Evolutionary epistemology is an approach that sees knowledge in the first place as a product of the variation and selection processes characterizing evolution. It notes, first, that the original function of knowledge is to make survival and reproduction of the organism that uses it more likely. Thus, organisms with better knowledge of their environments would have been preferred to organisms with less adequate knowledge. In that way, the phylogenetical evolution of knowledge depends on the degree to which its carrier survives natural selection through its environment. Popper, who spoke about "conjectures" and "refutations", and who noted that a fundamental criterion for every scientific theory is that it must be "falsifiable", i.e. able to undergo selection. The whole spectrum of evolutionary knowledge processes, from genetic mutation to scientific model-building, was first analysed by Donald T. Campbell, who also introduced the term "Evolutionary Epistemology".
To this basic framework, we must add a more detailed analysis of the different mechanisms of variation that create new ideas, of the way in which retained knowledge is stored and organized (knowledge representation), and of the different criteria that determine which knowledge will be selected and which one will be eliminated.
of Selection Theory and Evolutionary Epistemology
Vicarious Selectors
Author: F. Heylighen, & C. Joslyn,
Updated: Jul 14, 1995
Filename: VICARSEL.html
Knowledge is a mechanism that makes systems more efficient in surviving
different circumstances, by short cutting the purely blind variation and
selection they have to do. Knowledge Selection Criteria
Author: F. Heylighen,
Updated: Sep 10, 1997
Filename: KNOWSELC.html
Whereas traditional epistemologies try to distinguish "true" knowledge from "false" knowledge by postulating one or a few unambiguous "justication" criteria (e.g. correspondence, coherence, consensus), in an evolutionary context we must admit that many different influences impinge on the evolution of knowledge. It is well-recognized from observations of concrete ecosystems and from computer simulations of complex evolutionary systems, that evolution is basically co-evolution of many different systems with complicated interactions, where system A tries to adapt to B, while B tries to adapt to A. This makes it very difficult to formulate fixed and objective criteria distinguishing "fit" systems from "unfit" ones.
However, the definition of knowledge as a vicarious selector helping an organism to survive by anticipating perturbations, to some degree focuses the selection processes on the capacity of knowledge for prediction. Still, there are many different ways in which knowledge can support survival, and the predictive value can generally only be determined indirectly. This brings us to distinguish a number of different, mostly independent categories or dimensions, which each may contribute to the "fitness" of a piece of knowledge for its task, but which are not necessarily mutually consistent. The more a piece of knowledge fulfills each criterion separately, and the more criteria it fulfills in total, the better it is.
Thus, the criteria embody our "holistic" understanding of knowledge, which avoids reduction to either objective, subjective or social requirements, but acknowledges the roles that each of these realms plays in the spread of a successful piece of knowledge.
.
Selection Criteria for the Evolution of Knowledge", in: Proc. 13th Int. Congress on Cybernetics (Association Internat. de Cybernetique, Namur), p. 529.
Distinctiveness
Author: F. Heylighen,
Updated: Sep 5, 1995
Filename: DISTINCTV.html
Knowledge consists of distinctions. A distinction is useful only insofar that it can be used to predict some
deviation or variation from equilibrium. This entails that some change must follow or precede the appearance of the distinguished
phenomenon; phenomena that do not make any difference, are not informative,
and, hence, are not considered to be real in any practical sense. In other words, we need a "difference that makes a difference". For example, a sudden perturbation of the image on your retina because of dust in your eye will not be perceived as a distinct phenomenon. This requirement
corresponds to Kelley's (1967) distinctiveness criterion for
distinguishing "real" from "illusory" perceptions. Invariance
Author: F. Heylighen,
Updated: Sep 5, 1995
Filename: INVARIAN.html
The change following or preceding a distinguished phenomenon must not be unique, but
share some properties with changes associated with similar phenomena. A minimal
regularity or invariance of effect is needed in order to make
predictions (Heylighen, 1989). The invariance criterion can be subdivided in a
number of more specific criteria, specifying under which transformations of
initial phenomena (causes) the characteristics of the effect will be invariant.
The simplest type of invariance is probably that over time
("consistency" according to Kelley, 1967): subsequent appearances of the
distinguished phenomenon should lead to similar effects. An effect can also be
invariant over settings or circumstances, or over different points of
view or modalities of perception. The more invariant the causal
relationship, the more generally reliable and applicable it is, the more
predictions can be made with it, and the more useful the corresponding piece of
knowledge is.
If the same phenomenon is perceived in different ways, or through different
senses (e.g. sight and touch), it is more likely to objectively exist, rather
than to be the effect of a malfunctioning perceptual system. Coherence
Author: F. Heylighen
Updated: Mar 18, 1998
Filename: COHERENC.html New ideas cannot just be assimilated as such: they must make sense with respect to what the subject already knows. Existing beliefs provide a "scaffolding" needed to support new ideas. This requirement for ideas to "fit in" the pre-existing cognitive system may be called coherence. Coherence as a criterion of truth is emphasized by the epistemology of constructivism, which is espoused by most cyberneticists, and emphasized in "second-order" cybernetics (von Foerster, 1996) and the theory of autopoiesis (Maturana & Varela, 1992). According to this philosophy, knowledge is not a passive mapping of outside objects (the reflection-correspondence view), but an active construction by the subject. That construction is not supposed to reflect an objective reality, but to help the subject adapt or "fit in" to the world which it subjectively experiences.
Thagard, P. (1989) Explanatory Coherence. Behavioral and Brain Sciences 12: 435-467.
Utility
Author: F. Heylighen,
Updated: Sep 5, 1995
Filename: INDUTIL.html
A piece of knowledge will not only be selected for its objective reliability but for the degree to which it helps to solve personal problems. From two equally reliable models, one about the movement of stars in the Andromeda galaxy, and one about the movement of stocks at a stock exchange, the second one will obviously be much more successful, since it can be directly used to further one's own well-being by making money. Utility can be defined as the degree to which a piece of knowledge increases the competence of the user of that knowledge to reach his or her goals or solve his or her problems. Specific goals or values can be ultimately derived from the fundamental value of increased fitness for the actor. So, utility in an evolutionary context can be translated as "contribution to individual fitness".
Conformity
Author: F. Heylighen,
Updated: Oct 3, 1997
Filename: CONFORM.html Synopsys:
Evolution, Selfishness and Cooperation; Selfish Memes and the Evolution of Cooperation,Journal of Ideas, Vol 2, # 4, pp 70-84.
Selection Criteria for the Evolution of Knowledge", in: Proc. 13th Int. Congress on Cybernetics (Association Internat. de Cybernetique, Namur), p. 529. Collective Utility
Author: F. Heylighen,
Updated: Oct 3, 1997
Filename: COLLUTIL.html
The group equivalent of individual usefulness may be called collective utility. Some forms of knowledge benefit the collective, while being useless for an isolated individual. Languages, traffic regulations, technical standards and moral codes are examples of cognitive entities that have value only for intersubjective purposes. Such collective ideas will be selected at the group level: groups having such beliefs will be more fit than groups lacking them. This is how the supernatural cosmologies characterizing archaic civilisations discussed by Campbell (1997) have been selected.
Authority
Author: F. Heylighen,
Updated: Oct 3, 1997
Filename: AUTHORIT.html
Complementary to the homogenizing influence of conformity, we find the diversifying effect of the division of labor. Because of their limited cognitive capacity, individuals within a complex society tend to specialize in a particular domain. As illustrated by (1994) computer simulation, this process of cognitive differentiation is driven by a positive feedback mechanism: individuals who were successful in solving a particular type of problem will get more of these problems delegated to them, and thus develop a growing expertise or authority in that domain. The backing of a recognized expert will contribute to the acceptance of a particular idea. This is the criterion of authority. Epistemological Constructivism
Author: F. Heylighen,
Updated: Nov 12, 1997
Filename: CONSTRUC.html
The epistemology of (second order) cybernetics and of the Principia Cybernetica Project is constructivist. Ernst von Glasersfeld defines radical constructivism by the following two basic principles:
The importance of constructivism is best understood by comparing it with the opposite, more traditional, approach in epistemology or cognitive science, which sees knowledge as a passive reflection of the external, objective reality. This implies a process of "instruction": in order to get such an image of reality, the subject must somehow receive the information from the environment, i.e. it must be "instructed". The naive view is that our senses work like a camera that just projects an image of how the world "really" is onto our brain, and use that image as a kind of map, an encoding in a slightly different format of the objective structure "out there". Such a view runs quickly into a host of conceptual problems, mainly because it ignores the infinite complexity of the world. Moreover, detailed observation reveals that in all practical cases, cognition does not work like that. It rather turns out that the subject is actively generating plenty of potential models, and that the role of the outside world is merely limited to reinforcing some of these models while eliminating others (selection).
Background
Constructivism has its roots in Kant's synthesis of rationalism and empiricism (see Epistemology: introduction), where it is noted that the subject has no direct access to external reality, and can only develop knowledge by using fundamental in-built cognitive principles ("categories") to organize experience. One of the first psychologists to develop constructivism was Jean Piaget, who developed a theory ("genetic epistemology") of the different cognitive stages through which a child passes while building up a model of the world. In cybernetics, constructivism has been elaborated by Heinz Von Foerster, who noted that the nervous system cannot absolutely distinguish between a perception and a hallucination, since both are merely patterns of neural excitation. The implications of this neurophysiological view were further developed by Maturana and Varela, who see knowledge as a necessary component of the processes of autopoiesis ("self-production") characterizing living organisms.Without Miracles:
Universal Selection Theory and the Second Darwinian Revolution.social constructivism", which sees knowledge solely as the product of social processes of communication and negotiation (the "social construction of reality"). We reject these positions are unduly restrictive, and take a much more pragmatic stance, where we note that the adequacy of knowledge depends on many different criteria, none of which has an absolute priority over the others. People can very well use incoherent models, over which there is no agreement with others, but which still are valuable for adaptation to a complex world. These criteria will include at least subjective coherence, intersubjective consensus, and (indirect) comparison with "objective" environment.
Constructivism links on the web
(Radical) Constructivism page
Constructivism: from philosophy to practice
Reflection-correspondence theory
Author: V. Turchin,
Updated: Sep 1991
Filename: REFCORR.html
[Node to be completed]Subject of knowledge: "I"
Author: V. Turchin,
Updated: Sep 1991
Filename: SUBJ.html
[Node to be completed]Intuition
Author: V. Turchin,
Updated: Sep 1991
Filename: INTUIT.html
[Node to be completed]Doubt
Author: V. Turchin,
Updated: Sep 1991
Filename: DOUBT.html
[Node to be completed]Language
Author: V. Turchin,
Updated: Oct 6, 1997
Filename: LANG.html Synopsys: Concrete language Abstract language Unformalized language Art Philosophy Formalized language Descriptive sciences Theoretical sciences, mathematics Message
Author: V. Turchin,
Updated: Sep 1991
Filename: MESSAGE.html
[Node to be completed]Symbol
Author: V. Turchin,
Updated: Sep 1991
Filename: SYMBOL.html
[Node to be completed]Sentence
Author: V. Turchin,
Updated: Sep 1991
Filename: SENTENCE.html
[Node to be completed]Parsing
Author: V. Turchin,
Updated: Sep 1991
Filename: PARSING.html
[Node to be completed]Syntax
Author: Turchin,
Filename: SYNTAX.html
[node to be completed]
Semantics
Author: V. Turchin,
Updated: Sep 1991
Filename: SEMANT.html
[Node to be completed]Meaning
Author: V. Turchin,
Updated: Sep 1991
Filename: MEANING.html
[Node to be completed]Command
Author: V. Turchin,
Updated: Sep 1991
Filename: COMMAND.html
[Node to be completed]Statement
Author: V. Turchin,
Updated: Oct 6, 1997
Filename: STATEM.html
For primitive cybernetic systems which have no model of the world,
the command language is the only language that can be received.
If a system has a model of the world, as in the case of a human being
or a robot, the message received may not restrict the actions of the system
directly, but change the model of the wrld used by it. This will, obviously,
influence its actions in an indirect way, and, possibly, not immediately.
We call such messages statements. The content and the meaning
of a statement is in the knowledge it passes to the receiver.
It must be noted that when we simply say 'knowledge' we mean only
its impact on the genration of predictions and do not distinguish
between true knowledge and false (erroneous) knowledge.Instrumental meaning
Author: V. Turchin,
Updated: Sep 1991
Filename: INSTMEAN.html
[Node to be completed]Concept
Author: V. Turchin,
Updated: Sep 1991
Filename: CONCEPT.html
[Node to be completed]Abstraction
Author: V. Turchin,
Updated: Sep 29, 1997
Filename: ABSTRACT.html
There are two aspects of the concept of abstraction, as it is used:
in the context of the modelling scheme *, and in the context
of metasystem transition in the language.Human language
Author: V. Turchin,
Updated: Sep 1991
Filename: HUMLANG.html
[Node to be completed]Neuronal vs. logical concepts
Author: V. Turchin,
Updated: Sep 1991
Filename: NEURLOG.html
[Node to be completed]Formalization
Author: V. Turchin,
Updated: Sep 1991
Filename: FORMALIZ.html
[Node to be completed]Four types of linguistic activities
Author: V. Turchin
Updated: Sep 1991
Filename: LINGACT.html [Node to be completed]
~ Concrete language Abstract language
~
~
Unformalized Art Philosophy
language
~
~
Formalized Descriptive Theoretical
language sciences sciences,
~ mathematics
Truth
Author: V. Turchin,
Updated: Oct 6, 1997
Filename: TRUTH.html
Since a statement is a generator of predictions,
it is true if it generates only true predictions. A statement that
does not produce any predictions is, by this definition,
true -- vacuously.
Most important statements can produce infinitely many predictions;
we call such statements theories. We cannot directly verify such
a statement -- we have to believe that it is true. Karl Popper
stressed that we can never prove a theory, we only can reject it
when it gives us false predictions. Creation of theories is, essentially,
an evolutionary process. They arise as products of the creative
human mind and compete for survival. Those producing more important
predictions (and promising to give even more) are selected for usage;
the others perish. (See Evolutionary approach to Epistemology
and Epistemological Constructivism.)
There is no criterion of truth other than its power to give
predictions. Since powers, like multidimensional vectors, are hard to
compare, there is no universal and absolute criterion of truth.Statement of infiniteness
Author: V. Turchin
Updated: Sep 1991
Filename: STATINF.html [Node to be completed]The law of the excluded middle
Author: V. Turchin
Updated: Sep 1991
Filename: EXMID.html [Node to be completed]Predicate
Author: V. Turchin
Updated: Sep 1991
Filename: PREDICAT.html [Node to be completed]Proof
Author: V. Turchin
Updated: Sep 1991
Filename: PROOF.html [Node to be completed]Verification
Author: V. Turchin
Updated: Sep 1991
Filename: VERIFIC.html [Node to be completed]
Testing process Prediction is
-------------------- ------------------
1. ends in success verifyably true
2. ends in failure verifyably false
3. never ends false, but this is not directly verifyable
Foundation of logic and mathematics
Author: V. Turchin
Updated: Sep 1991
Filename: LOGMATH.html [Node to be completed]Probability
Author: C. Joslyn, V. Turchin
Updated: Aug 1993
Filename: PROBAB.html [Node to be completed]Theories versus facts
Author: V. Turchin
Updated: Sep 1991
Filename: THEORIES.html [Node to be completed]Objectivity
Author: Turchin,
Updated: Sep 29, 1997
Filename: OBJECTIV.html
By objective description of the world we mean, first, a description
in terms of some objects, and second, a description which is,
as much as possible, ``objective'' in the usual sense, i.e.
impersonal, not depending on the cognitive actions, or other
features, of the subject of knowledge. The use of the same
word in these two meanings is not accidental: a description can be
``objective'' because it is a description in terms of objects.
Looking for objectivity is nothing else but
factoring out certain cognitive actions.
Function fa (see *Object*) factors out the action a by predicting
what should be observed when the only change in the world is
the subject's taking of the action a. If the prediction comes true,
we interpret this as the same kind of stability as when nothing changes
at all. The concept of object btings in a certain invariance, or stability,
in the perception of a cybernetic system that actively explores
its environment.Systems Concepts
Author: C. Joslyn, F. Heylighen, J. Bollen,
Updated: Jan 7, 1997
Filename: SYSCONC.html
Metasystem Transition Theory is founded on a thoroughly analyzed systems theoretic vocabulary of
concepts and terms. This conceptual basis is intended to be
both foundational and evolving, one aspect of a meta-foundational system.
Foundation of Mathematics
Author: Turchin,
Updated: Jun 24, 1997
Filename: FOUNDMAT.html
The philosophy developed in MST theory leads to a certain view
on the nature and workings of mathematics and gives certain answers
to the long-standing questions about the foundations of mathematics.
At present we have two documents on the foundation of logic
and mathematics in the light of our epistemology and ontology:
We plan to represent the contents of these documents in the format
of Principia Cybernetica. We hope that the work along these
lines will be discussed and continued.
R. Glueck & A. Klimov (1995): Metasystem Transitions in Computer Science and Mathematics (rtf format),"World Futures: the journal of general evolution 45, p. 213.What is complexity?
Author: F. Heylighen,
Updated: Dec 9, 1996
Filename: COMPLEXI.html
Complexity has turned out to be very difficult to define. The dozens of definitions that have been offered all fall short in one respect or another, classifying something as complex which we intuitively would see as simple, or denying an obviously complex phenomenon the label of complexity. Moreover, these definitions are either only applicable to a very restricted domain, such as computer algorithms or genomes, or so vague as to be almost meaningless. (1996) gives a good review of the different definitions and their shortcomings, concluding that complexity necessarily depends on the language that is used to model the system.
Still, I believe there is a common, "objective" core in the different concepts of complexity. Let us go back to the original Latin word complexus, which signifies "entwined", "twisted together". This may be interpreted in the following way: in order to have a complex you need two or more components, which are joined in such a way that it is difficult to separate them. Similarly, the Oxford Dictionary defines something as "complex" if it is "made of (usually several) closely connected parts". Here we find the basic duality between parts which are at the same time distinct and connected. Intuitively then, a system would be more complex if more parts could be distinguished, and if more connections between them existed.
More parts to be represented means more extensive models, which require more time to be searched or computed. Since the components of a complex cannot be separated without destroying it, the method of analysis or decomposition into independent modules cannot be used to develop or simplify such models. This implies that complex entities will be difficult to model, that eventual models will be difficult to use for prediction or control, and that problems will be difficult to solve. This accounts for the connotation of difficult, which the word "complex" has received in later periods. (1996) notes that the definition of complexity as midpoint between order and disorder depends on the level of representation: what seems complex in one representation, may seem ordered or disordered in a representation at a different scale. For example, a pattern of cracks in dried mud may seem very complex. When we zoom out, and look at the mud plain as a whole, though, we may see just a flat, homogeneous surface. When we zoom in and look at the different clay particles forming the mud, we see a completely disordered array. The paradox can be elucidated by noting that scale is just another dimension characterizing space or time (Havel, 1995), and that invariance under geometrical transformations, like rotations or translations, can be similarly extended to scale transformations (homotheties). References:
is Complexity?", in: F. Heylighen & D. Aerts (eds.), The Evolution of Complexity (Kluwer, Dordrecht).
See also:
Foundational Concepts
Author: C. Joslyn,
Updated: Jan 1992
Filename: FOUNDCONC.html
[Node to be completed]Actions
Distinctions
Subject
Evolutionary Theory
Author: F. Heylighen,
Updated: Jan 27, 1997
Filename: EVOLUT.html
We see evolution as based on the trial-and-error process of variation and natural selection of systems at all levels of complexity. The name of 'natural selection' comes from the Darwinian theory of biological evolution, which distinguishes "natural" selection from "artificial" selection, where specific features are retained or eliminated depending on a goal or intention (e.g. the objective of a cattle breeder who would like to have cows that produce more milk). The "implicit goal" of natural selection is maintenance or reproduction of a configuration at some level of abstraction. The selection is natural in the sense that there is no actor or purposive system making the selection. The selection we are discussing is purely automatic or spontaneous, without plan or design involved. Selection or self-organization?
Many criticisms have been and are being raised against the Darwinian view of evolution. We will here not discuss the criticisms stating that there are designs or plans guiding evolution, but focus on a more recent upsurge of people, many of whom are associated with the systems movement, who state that natural selection must be complemented by self-organization in order to explain evolution. (see e.g. Jantsch, 1979; Kauffman, 1993; Swenson, 19). However, we must not confuse the specific theory of Darwinian evolution with the general principle of natural selection.
Like Swenson (19) notes, it cannot explain the evolution of a "population of one". In our present, more general interpretation, there is no need for competition between simultaneously present configurations. A configuration can be selected or eliminated independently of the presence of other configurations: a single system can pass through a sequence of configurations, some of which are retained while others are eliminated (see the Principle of Selective Retention). The only "competition" involved is one between subsequent states of the same system. Such selection can still be "natural". Self-organization
Author: F. Heylighen
Updated: Jan 27, 1997
Filename: SELFORG.html Synopsys: F. Heylighen: "Self-Organization, Emergence and the Architecture of Complexity".
Entropy and the Laws of Thermodynamics
Author: J. de Rosnay
Updated: Jul 3, 1998
Filename: ENTRTHER.html The principal energy laws that govern every organization are derived
from two famous laws of thermodynamics. The second law, known as Carnot's
principle, is controlled by the concept of entropy.
Today the word entropy is as much a part of the language of the physical sciences as it is of the human sciences. Unfortunately, physicists, engineers, and sociologists use indiscriminately a number of terms that they take to be synonymous with entropy, such as disorder, probability, noise, random mixture, heat; or they use terms they consider synonymous with antientropy, such as information, neguentropy, complexity, organization, order, improbability.
There are at least three ways of defining entropy:
The first law of thermodynamics says that the total quantity of energy in the universe remains constant. This is the principle of the conservation of energy. The second law of thermodynamics states that the quality of this energy is degraded irreversibly. This is the principle of the degradation of energy.
The first principle establishes the equivalence of the different forms of energy (radiant, chemical, physical, electrical, and thermal), the possibility of transformation from one form to another, and the laws that govern these transformations. This first principle considers heat and energy as two magnitudes of the same physical nature
About 1850 the studies of Lord Kelvin, Carnot, and Clausius of the exchanges of energy in thermal machines revealed that there is a hierarchy among the various forms of energy and an imbalance in their transformations. This hierarchy and this imbalance are the basis of the formulation of the second principle.
In fact physical, chemical, and electrical energy can be completely changed into heat. But the reverse (heat into physical energy, for example) cannot be fully accomplished without outside help or without an inevitable loss of energy in the form of irretrievable heat. This does not mean that the energy is destroyed; it means that it becomes unavailable for producing work. The irreversible increase of this nondisposable energy in the universe is measured by the abstract dimension that Clausius in 1865 called entropy (from the Greek entrope, change).
The concept of entropy is particularly abstract and by the same token difficult to present. Yet some scientists consider it intuitively; they need only refer mentally to actual states such as disorder, waste, and the loss of time or information. But how can degraded energy, or its hierarchy, or the process of degradation be truly represented?
There seems to be a contradiction between the first and second principles. One says that heat and energy are two dimensions of the same nature; the other says they are not, since potential energy is degraded irreversibly to an inferior, less noble, lower-quality form--heat. Statistical theory provides the answer. Heat is energy; it is kinetic energy that results from the movement of molecules in a gas or the vibration of atoms in a solid. In the form of heat this energy is reduced to a state of maximum disorder in which each individual movement is neutralized by statistical laws.
Potential energy, then, is organized energy; heat is disorganized energy. And maximum disorder is entropy. The mass movement of molecules (in a gas, for example) will produce work (drive a piston). But where motion is ineffective on the spot and headed in all directions at the same time, energy will be present but ineffective. One might say that the sum of all the quantities of heat lost in the course of all the activities that have taken place in the universe measures the accumulation of entropy.
One can generalise further. Thanks to the mathematical relation between disorder and probability, it is possible to speak of evolution toward an increase in entropy by using one or the other of two statements: "left to itself, an isolated system tends toward a state of maximum disorder" or "left to itself, an isolated system tends toward a state of higher probability." These equivalent expressions can be summarized:
The concepts of entropy and irreversibility, derived from the second principle, have had a tremendous impact on our view of the universe. In breaking the vicious circle of repetitiveness in which the ancients were trapped, and in being confronted with biological evolution generating order and organization, the concept of entropy indirectly opens the way to a philosophy of progress and development. At the same time it introduces the complementarity between the "two great drifts of the universe" described in the works of Bergson and Teilhard de Chardin.
The image of the inexorable death of the universe, as suggested by the second principle, has profoundly influenced our philosophy, our ethics, our vision of the world, and even our art. The thought that by the very nature of entropy the ultimate and only possible future for man is annihilation has infiltrated our culture like a paralysis. This consideration led Leon Brillouin to ask, "How is it possible to understand life when the entire world is ordered by a law such as the second principle of thermodynamics, which points to death and annihilation?"
See also:
Entropy and Information Theory on the Web
| Synopsys: |
According to the neo-Darwinist view, evolution takes place through the creation of random combinations of matter, with the subsequent struggle for existence, as a result of which some combinations survive and proliferate, while other perish. Popper describes this as the work of the general method of trial and error-elimination. Campbell uses the term blind variation and selective retention. Newell and Simon in their theory of problem solving called this mechanism "generate and test". Here we will speak simply of the trial and error method.
We do not need to use the term `blind', because in cultural evolution or in problem solving we often have informed and guided choices. But even with regard to biological evolution we cannot be sure, much less prove, that the variation is blind. It is true that we build our theory and check it against facts in the assumption that variations are blind. But we do not really use the fact that the variation is, indeed, blind or random, i.e. all choices physically and logically possible are equiprobable. The success of the theory proves that blindness, at the present state of the theory, is sufficient, but does not prove it is necessary. The main requirement is that a large number of possible states or solutions is explored through a process of variation.
The principle is so powerful that any type of variation or trial, whether guided by foreknowledge or not, followed by the elimination of the "bad", or "unfit" trials, and the retention or propagation of the "fit" trials, will result in evolution. The fact that succesful steps are retained leads to an irreversible accumulation, a "ratchet effect" which only allows movement in a particular general direction, without going back (see the principle of asymmetric transitions).
Variety has always been a fundamental idea in Cybernetics and Systems Science, and is so in Metasystem Transition Theory. Variety is defined as a multiplicity of distinctions. The existence of variety is necessary for all change, choice, and information.
Frequently the quantity of variety and the change in the quantity of variety (positive increase or negative decrease) is critical to understand system evolution. Where variety is manifest in a process, then we sometimes want to say that there is uncertainty about the outcome of the process; when that uncertainty is relieved but the occurrence of one of the possibilities, then we gain information. The are many possible ways to measure the quantity of variety, uncertainty, or information \cite{KLGFOT87}. The simplest is the count of the number of distinctions. More useful can be the logarithm of that number as a quantity of information, which is called the Hartley entropy. When sets and subsets of distinctions are considered, possibilistic nonspecificities result \cite{KLG84a}. The most celebrated are the stochastic entropies of classical information theory, which result from applying probabilistic distributions to the various distinctions. A reduction in the quantity of variety is the process of selection.
Selection processes are endemic in systems theories. The most significant is the natural selection of Darwinian evolution, but in this context we can recognize natural selection outside of the context of biological evolution as any selection process which eliminates distinctions. Also included in the concept of selection are all forms of stability and equilibrium.
Variation on its own, without further constraints, produces entropy or disorder, by diffusion of existing constraints or dependencies. The equivalent for DNA is called "genetic drift".
However, variation is generally held in check by selection. Selection is the elimination or reduction of part of the variety of configurations produced by variation. Selection decreases disorder or entropy, by reducing the number of possibilities (Heylighen, 1992). A system that undergoes selection is constrained: it is restricted in the number of variations it can maintain. The existence of selection follows from the fact that in general not all variants are equivalently stable or capable of (re)production: those that are more easy to maintain or generate will become more numerous relative to the others (Heylighen, 1992). If all possible configurations are equally likely to be produced or conserved, there is no selection, and the only possible outcome of the process is maximization of statistical entropy, as in the cloud of gas molecules that diffuses to homogeneously fill its container. Selection can be internal, as when an unstable system (e.g. a radio-active atom) spontaneously annihilates, or external, as when a system is eliminated because it is not adapted to its environment (Heylighen, 1991a). Fitness is a measure of the likeliness that a configuration will be selected.
Although this technical interpretation may seem rather far removed from the intuitive notion, the English word "fit" is eminently suited for expressing the underlying dynamic. Its spectrum of meanings ranges between two poles: 1) "fit" as "strong", "robust", "in good condition"; 2) "fit" as "adapted to", "suited for", "fitting". The first sense, which may be called "absolute fitness", points to the capability to survive internal selection, i.e. intrinsic stability and capacity for (re)production. The second sense, which may be called "relative fitness", refers to the capability to survive external selection, i.e. to cope with specific environmental perturbations or make use of external resources.
It must be noted that "internal" and "external" merely refer to complementary views of the same phenomenon. What is internal for a whole system, may be external for its subsystems or components. For example, the concentration of oxygen in the air is an external selective factor for animals, since in order to survive they need a respiratory system fit to extract oxygen. Similarly, the concentration of carbon dioxide is an external selective factor for plants. However, when we consider the global ecosystem consisting of plants and animals together, we see that the concentrations of both oxygen and carbon dioxide are internally determined, since oxygen is produced out of carbon dioxide by plants, and carbon dioxide out of oxygen by animals. Survival of the global system requires an internal "fit" of the two halves of the carbon dioxide - oxygen cycle: if more oxygen or carbon dioxide would be consumed than produced, the whole system would break down.
Similarly, when we look at a crystal as whole system, we see it as a stable structure that is unlikely to disintegrate, i.e. it is absolutely fit and survives internal selection. However, when we look at the molecules as the parts that make up the crystal, we see that they must have the right connections or bonds, i.e. fit relations, to form a stable whole. The exact configuration of each molecule is externally selected by the other molecules to which it must fit. In this way, every absolute or intrinsic fitness characterizing a whole can be analysed as the result of a network of interlocking relational fitnesses connecting the parts .
In summary, a system will be selected if: 1) its parts "fit together", i.e. form an intrinsically stable whole, 2) the whole "fits" its environment, i.e. it can resist external perturbations and profit from external resources to (re)produce.
Biological evolution is a very complex process. Using mathematical modeling, one can try to clarify its features. But to what extent can that be done? For the case of evolution, it seems unrealistic to develop a detailed and fundamental description of phenomena as it is done in theoretical physics. Nevertheless, what can we do? Can mathematical models help us to systemize our knowledge about evolution? Can they provide us with more a profound understanding of the particularities of evolution? Can we imagine (using mathematical representation) some hypothetical stages of evolution? Can we use mathematical models to simulate some kind of artificial "evolution"?
In order to clarify such questions, it is natural to review the already developed models in a systematic manner. In evolutionary modeling one can distinguish the following branches:
Quasispeciesis a model of a Darwinian evolution of a population of the polynucleotide strings (analogous to RNA), which are supposed to have certain replication abilities. Polynucleotide strings are modeled by informational sequences. The model implies that there is a master sequence, having a maximal selective value (a selective value is a sequence fitness). The selective values of other sequences are defined as follows: the more similar is the particular sequence to the master sequence, the greater is its selective value. The evolution process includes the selection (according to the selective values) and the mutations of informational sequences. The final result of an evolution is a quasispecie, that is the distribution of sequences in the neighborhood of the master sequence.
The model of quasispecies was analyzed mathematically by a number of authors [1-6], and the particularities, concerning a final sequence distribution, a restriction on the sequence length, and a rate of evolution were quantitatively estimated. A short review of these mathematical results as well as a formal description of the model are given in the child node quasispecies.
M.Eigen et al interpreted quasispecies as a model of a primitive RNA-sequences origin. Taking into account the nucleotide coupling abilities, they deduced that the length of these primitive RNA-sequences could not be greater than 100 nucleotides. As the further stage of macromolecular evolution, M.Eigen and P.Schuster proposed a model of hypercycles, which include the polynucleotide RNA-sequences as well as polypeptide enzymes [2].
Hypercycle is a self-reproducing macromolecular system, in which RNAs and enzymes cooperate in the following manner: there are n RNAs; i-th RNA codes i-th enzyme (i = 1,2,...,n); the enzymes cyclically increase RNA's replication rates, namely, 1-st enzyme increases replication rate of 2-nd RNA, 2-nd enzyme increases replication rate of 3-rd RNA, ..., n-th enzyme increases replication rate of 1-st RNA; in addition, the described system possesses primitive translation abilities, so the information stored in RNA-sequences is translated into enzymes, analogously to the usual translation processes in biological objects. For effective competition (i.e. for surviving the hypercycle with greatest reaction rate and accuracy), the different hypercycles should be placed in separate compartments, for example into A.I.Oparin's coacervates [7]. M.Eigen and P.Schuster consider hypercycles as predecessors of protocells (primitive unicellular biological organisms) [2]. As quasispecies, hypercycles were also analyzed mathematically in details. The child node hypercycles describes formally this model.
The models of quasispecies and hypercycles were rather well developed and provide certain consequent description of hypothetical process of first molecular-genetic system origin. But they are not unique. The life origin problem is very intriguing, and there is diversity of this problem investigations. We mention here only some of them.
F.H.C.Crick discussed in details the possible steps of genetic code origin [8].
F.J.Dyson proposed the model of "phase transition from chaos to order" to interpret the stages of cooperative RNA-enzyme systems origin [9].
P.W.Anderson et al used the physical spin-glass concept in order to model a simple polynucleotide sequence evolution [10]. This model is similar to the quasispecies.
H.Kuhn considered the creation of the aggregates of RNAs as a stage for an origin of a simple ribosome-like translation device [11].
So, the approaches to the molecular-genetic system origin modeling are different in many relations. However, some convergence points do exist. In the early 1980s, V.A.Ratner and V.V.Shamin (Novosibirsk, Russia), D.H.White (California), and R.Feistel (Berlin) independently proposed the same model [12-14]. V.A.Ratner called it "syser" (the abbreviation from SYstem of SElf-Reproduction).
Syser is a system of catalytically interacting macromolecules, it includes the polynucleotide matrix and several proteins; there are two obligatory proteins: the replication enzyme and the translation enzyme; syser can also include some structural proteins and additional enzymes. The polynucleotide matrix codes proteins, the replication enzyme provides the matrix replication process, the translation enzyme provides the protein synthesis according to an information coded in the matrix; structural proteins and additional enzymes can provide optional functions. Analogously to hypercycles, different sysers should be inserted into different compartments for effective competition. Mathematical description of sysers (see Sysers for details) is similar to that of hypercycles.
As compared with hypercycles, sysers are more similar to simple biological organisms. The concept of sysers provides the ability to analyze evolutionary stages from a mini-syser, which contains only matrix and replication and translation enzymes, to protocells, having rather real biological features. For example, "Adaptive syser" [15] includes a simple molecular control system, which "turns on" and "turns off" synthesis of some enzyme in response to the external medium change; the scheme of this molecular regulation is similar to the classical model by F.Jacob and J.Monod [16]. The control system of the adaptive syser could be the first control system, which was "invented" by biological evolution.
Additionally, it should be noted, that the scheme of sysers is similar to that of the Self-Reproducing Automata, which were proposed and investigated at the sunrise of modern computer era by J.von Neumann [17].
Conclusion. The considered models of course can't explain the real life origin process, because these models are based on various plausible assumptions rather than on a strong experimental evidences. Nevertheless, quasispecies, hypercycles, and sysers provide a well defined mathematical background for understanding of the first molecular-genetic systems evolution. These models can be used to develop the scenarios of the first cybernetic systems origin, they can be juxtaposed with biochemical data to interpret qualitatively the corresponding experiments, and can be considered as a step for developments of more powerful models.
References:
1. M.Eigen. Naturwissenshaften. 1971. Vol.58. P. 465.
2. M.Eigen, P.Schuster. "The hypercycle: A principle of natural self-organization". Springer Verlag: Berlin etc. 1979.
3. C.J.Tompson, J.L.McBride. Math. Biosci. 1974. Vol.21. P.127.
4. B.L.Jones, R.H.Enns, S.S. Kangnekar. Bull. Math. Biol. 1976. Vol.38. N.1. P.15.
5. Von H.D.Fosterling, H.Kuhn, K.H.Tews. Ang. Chem. 1972. Jg.84. Nr.18. S. 862.
6. V.G.Red'ko. Biofizika. 1986. Vol. 31. N.3. P. 511 (In Russian).
7. A.I.Oparin. "The origin of life". New York, 1938. A.I.Oparin. "Genesis and evolutionary development of life". New York, 1968.
8. F.H.C.Crick. J. Mol. Biol. 1968. Vol. 38. N.3. P.367.
9. F.J.Dyson. J. Mol. Evol. 1982. Vol.18. N.5. P.344.
10. P.W.Anderson. Proc. Natl. Acad. Sci. USA. 1983. V.80. N.11. P.3386. Rokhsar D.S., Anderson P.W., Stein D.L. J.Mol. Evol. 1986. V.23. N.2. P.119.
11. H.Kuhn. Angew. Chem. 1972. Jg.84. Nr.18. S.838.
12. V.A.Ratner and V.V.Shamin. In: Mathematical models of evolutionary genetics. Novosibirsk: ICG, 1980. P.66. V.A.Ratner and V.V.Shamin. Zhurnal Obshchei Biologii. 1983. Vol.44. N.1. PP. 51. (In Russian).
13. D.H.White. J. Mol. Evol. 1980. Vol.16. N.2. P.121.
14. R.Feistel. Studia biophysica.1983. Vol.93. N.2. P.113.
15. V.G.Red'ko. Biofizika. 1990. Vol. 35. N.6. P. 1007 (In Russian).
16. F.Jacob and J.Monod. J. Mol. Biol. 1961. Vol. 3. P. 318.
17. J.von Neumann, A. W. Burks. "Theory of self-reproducing automata". Univ. of Illinois Press, Urbana IL, 1966.
Sequences are the model "organisms", they have certain (nonnegative) selective values fk = f(Sk). We assume here, that there is the master sequence Sm , having the maximal selective value. The selective value of any sequence depends only on Hamming distance (the number of different symbols at corresponding places in sequences) between given S and master sequence Sm : f(S) = f(r(S,Sm)) - the smaller is the distance r , the greater is the selective value f . For simplicity we assume here, that values f are not greater than 1.
The evolution process consists of consequent generations. New generation {Sk (t+1)} is obtained from the old one {Sk(t)} by selection and mutations of sequences Sk (t) ; here t is the generation number. The model evolution process can be described formally in the following computer-program-like manner.
| Step 0. (Formation of an initial population {Sk (0)} ) For every k = 1 , ..., n, for every i = 1 , ..., N , choose randomly a symbol Ski by setting it to an arbitrary symbol from given alphabet. | |
| Step 1. (Selection) |
| Substep 1.1. (Selection of a particular sequence). Choose randomly a sequence number k*, and select the sequence Sk*(t) (without canceling it from the old population) into the new population {Sk(t+1)} with the probability fk* = f (Sk* (t)). | |
| Substep 1.2. (Iteration of the sequences selection, control of the population size). Repeat the substep 1.1 until the number of sequences in the new population reaches the value n . |
| Step 2. (Mutations) For every k = 1 , ..., n, for every i = 1 , ..., N , change with the probability P the symbol Ski(t+1) to an arbitrary other symbol of the alphabet. | |
| Step 3. (Organization of the iterative evolution). Repeat the steps 1, 2 for t = 0, 1, 2, ... |
The evolution character depends strongly on the population size n. If n is very large (n >> lN ), the numbers of all sequences in a population are large and the evolution can be considered as deterministic process. In this case the population dynamics can be described in terms of the ordinary differential equations and analyzed by well known methods. The main result of such an analysis [1-4] are the following conclusions: 1) the evolution process always converges, and 2) the final population is a quasispecie, that is the distribution of the sequences in the neighborhood of the master sequence Sm.
In the opposite case (lN >> n), the evolution process is essentially stochastic, and computer simulations as well as reasonable quantitative estimations can be used to characterize the main evolution features [1,2,5]. At large sequence length N (N > 50) we have just this case for any real population size.
The main evolution features and the estimations in the stochastic case for two-letter alphabet ( l = 2; Ski = 1, -1 ) are described in the child node Estimation of the evolution rate . It is shown that the total number of generations T , needed to converge to a quasispecie at sufficiently large selection intensity, can be estimated by the value
| T ~ (N/2)x(PN)-1, | (1) |
where P is a mutation intensity. This estimation implies a sufficiently large population size
| n > T, | (2) |
at which the effect of the neutral selection [6] can be neglected (see Estimation of the evolution rate, Neutral evolution game for details).
It is interesting to estimate, how effective can be an evolution algorithm of searching. Namely, what is a minimal value of the total number of participants ntotal = nT , which are needed to find a master sequence in evolution process? According to (1) , (2) , to minimize ntotal , we should maximize the mutation intensity P . But at large P , the already found "good" sequences could be lost. "Optimal" mutation intensity P ~ N -1 corresponds approximately to one mutation in any sequence per generation. Consequently, we can conclude that an "optimal" evolution process should involve of the order of
| ntotal = nT ~ N 2 | (3) |
participants, to find the master sequence.
This value can be compared with the participant number in deterministic and pure random methods of search. The simple deterministic (sequential) method of search (for the considered Hamming-distance-type selective value and two-letter alphabet, Si = 1, -1 ) can be constructed as follows: 1) start with arbitrary sequence S , 2) try to change consequently its symbols: S1 --> - S1 , S2 --> - S2 , ... , by fixing only such symbol changes, those increase the sequence selective value. The total number of sequences, which should be tested in order to find the master sequence Sm in such a manner, is equal to N : ntotal = N . In a pure random search, to find Sm , we need to inspect of the order of 2N sequences : ntotal ~ 2N .
So, we have the following estimations:
Deterministic search
ntotal = N
Evolutionary search
ntotal ~ N 2
Random search
ntotal ~ 2N
Thus, for simple assumptions (Hamming-distance-type selective value and two-letter alphabet), the evolution method of search is essentially more effective than the random one, but it is something worse as compared with the deterministic search.
The Hamming-distance-type model implies that there is unique maximum of the selective value. This is a strong restriction. Using the spin-glass concept (see Spin-glass model of evolution), it is possible to construct a similar model of informational sequences evolution for the case of very large number of the local maxima of a selective value. The evolution rate, restriction on population size, and total number of evolution participants in that model can be also roughly estimated by formulas (1) - (3). But unlike the Hamming-distance model, the spin-glass-type evolution converges to one of the local selective value maxima, which depends on a particular evolution realization.
Conclusion. Quasispecies describes quantitatively a simple information sequence evolution in terms of sequence length, population size, and mutation and selection intensities. This model can be used to characterize roughly the hypothetical prebiotic polynucleotide sequence evolution and to illustrate mathematically general features of biological evolution.
References:
1. M.Eigen. Naturwissenshaften. 1971. Vol.58. P. 465.
2. M.Eigen, P.Schuster. "The hypercycle: A principle of natural self-organization". Springer Verlag: Berlin etc. 1979.
3. C.J.Tompson, J.L.McBride. Math. Biosci. 1974. Vol.21. P.127.
4. B.L.Jones, R.H.Enns, S.S. Kangnekar. Bull. Math. Biol. 1976. Vol.38. N.1. P.15.
5. V.G.Red'ko. Biofizika. 1986. Vol. 31. N.3. P. 511. V.G.Red'ko. Biofizika. 1990. Vol. 35. N.5. P. 831 (In Russian).
6. M. Kimura. "The neutral theory of molecular evolution". Cambridge Un-ty Press. 1983.
We consider the stochastic case (lN >> n) under the following simplifying assumptions:
| 1) the alphabet consists of two letters (l = 2), namely, sequence symbols take the values: Ski = 1, -1; k = 1,..., n ; i = 1,..., N ; | |
| 2) the selective value of any sequence S is defined as: |
| f(S) = exp[-b r(S,Sm)], | (1) |
| where b is a selection intensity parameter, r(S,Sm) is the Hamming distance between the given sequence S and the master sequence Sm ; | |
| 3) the mutation intensity P , that is the probability to reverse a sign of any symbol (Ski --> - Ski) during mutations, is sufficiently small: |
PN  b,
1. |
(2) |
Note, that for large P , the already found "good" sequences could be lost, so the inequality (2) is a condition for the successful evolutionary search of the sequences with large selective values (see [1,2] for details). The inequality (2) implies also a rather large selection intensity.
In addition, we assume that the population size n is sufficiently large, so a neutral selection effect [3] can be neglected (see below for the more detailed consideration).
Fig. 1 illustrates schematically the sequence distribution dynamics during the evolution process. Here n(r) is the number of sequences S , such that r(S,Sm) = r in a considered population; t is the generation number.
Fig. 1. The sequence distribution n(r) at different generations t ; t3 > t2 > t1 (schematically, according to the computer simulations [2]).
The initial sequence distribution (t = 0) is a random one, it spreads in the vicinity of the value r0 = N/2 (r0 is the mean distance between an arbitrary sequence S and the master one Sm). The sequences with small r , having large selective values, are absent in the initial population. At the first several generations, the sequences, having maximal available in initial population selective value (corresponding to the left edge of the distribution at t = 0), are quickly selected, and the distribution becomes more narrow than the initial one. Such a distribution is shown in Fig.1 by the curve at t1 .
At further generations the distribution is shifted to the left (the curves at t2 , t3) until the final distribution (placed near r = 0) is reached. Because the selection intensity b is rather large (see (2)), the "shift" process is limited mainly by mutations. Typically of the order of dt = (PN)-1 generations (dt is typical time for one mutation per sequence) are needed to shift the distribution to the left on the value dr = 1. So, we can estimate the total number of evolution generations by the value
| T ~ dt x (N/2)/dr ~ (N/2)x(PN)-1. | (3) |
Eq. (3) characterizes roughly the evolution rate.
So far we have neglected the neutral selection effect, which is essential at a small population size [3]. The neutral selection is the random fixation in a population an arbitrary "species", regardless of a selective value. It could suppress the search of the "good" sequences. Typical time Tn of neutral selection is of the order of a population size n (see Neutral evolution game for details). We can neglect the neutral selection, if the total generation number T is smaller than Tn :
| T < Tn ~ n . | (4) |
The inequality (4) is a condition, at which the estimation of the evolution rate (3) is valid.
In addition, we can construct the "optimal" evolution process, which involves the minimal total number of participants ntotal = nT under condition that master sequence is found. The "optimal" evolution corresponds to the maximal permissible mutation intensity P ~ N -1 (see (2)). At this P , according to (3), we have T ~ (N/2) . Taking into account (4), we can set n ~ 2N and obtain finally:
| ntotal = nT ~ N 2 | (5) |
The estimation (5) characterizes the effectiveness of the evolution process as an algorithm for search of the optimal (master) sequence.
The estimations (3), (5) were confirmed by computer simulations [2].
References:
1. M.Eigen, P.Schuster. "The hypercycle: A principle of natural self-organization". Springer Verlag: Berlin etc. 1979.
2. V.G.Red'ko. Biofizika. 1986. Vol. 31. N.3. P. 511. V.G.Red'ko. Biofizika. 1990. Vol. 35. N.5. P. 831 (In Russian).
3. M. Kimura. "The neutral theory of molecular evolution". Cambridge Un-ty Press. 1983.
Neutral selection plays an important role in the evolution of populations, having a finite population size n [1] . To demonstrate the neutral selection features explicitly, let's consider the pure neutral evolution game, which is defined as follows:
| 1. There is a population of black and white balls, the total number of the balls in a population is equal to n . | |
| 2. The evolution consists of consequent generations. Each generation consists of two steps. At the first step we duplicate each ball, conserving its color: a black ball has two black offsprings, a white ball has two white ones. At the second step we randomly remove from a population exactly half of the balls with equal probability for black and white "species", independently of their color. |
We say that the population is in l -state, if the numbers of black and white balls at a considered generation are equal to l and n-l, respectively. We can characterize the evolution by the probability Plm of a transition from l -state to m -state during one generation. Using a straightforward combinatorial consideration, we can calculate the values of Plm :
The matrix Plm determines the random Markovian process, which can be considered as an example of a simple stochastic genetic process [2]. Using the general methods of analysis of such processes [2], we can deduce that:
1) the considered process always converges to one of two absorbing states, namely, to 0-state (all balls are white), either to n-state (all balls are black);
2) at large n the characteristic number of generations Tn , needed to converge to the either absorbing state, is equal to 2n :
| Tn = 2n . | (2) |
Thus, although this evolution is purely neutral (black and white balls have equal chances to survive), nevertheless only one species is selected. The value Tn characterizes the neutral selection rate, it is used in our estimations (Quasispecies , Estimation of the evolution rate).
References:
1. M. Kimura. "The neutral theory of molecular evolution". Cambridge Un-ty Press. 1983.
2. S. Karlin. "A first course in stochastic processes". Academic Press. New York, London, 1968.
The model of evolution, discussed in Quasispecies, implies a strong assumption: the selective value is determined by the Hamming distance between the particular and unique master sequences. Only one maximum of the selective value exists. Using the physical spin-glass concept, we can construct a similar model for a very large number of the local maxima of a selective value.
D. Sherrington and S. Kirkpatrick proposed a simple spin-glass model to interpret the physical properties of the systems, consisting of randomly interacting spins [1]. This well-known model can be described shortly as follows:
| 1) There is a system S of spins Si , i = 1,..., N (the number of spins N is supposed to be large, N >> 1). Spins take the values: Si = 1, -1 . | |
| 2) The exchange interactions between spins are random. The energy of the spin system is defined as: |
| E (S) = - Si<j Jij Si Sj , | (1) |
| where Jij are the exchange interactions matrix elements. Jij are normally distributed random values: |
| Probability_density{Jij } = (2p)-1/2 (N-1)1/2 exp [- Jij2 (N-1)2-1] . | (2) |
From (1), (2) one can obtain, that the mean spin-glass energy is zero (<E > = 0) , and the mean square root value of the energy variation at one-spin reversal is equal to 2:
| MSQR {dE (Si --> - Si) } = 2 . | (3) |
The model (1), (2) was intensively investigated. For further consideration the following spin-glass features are essential :
- the number of local energy minima M is very large: M ~ exp(aN) , a = 0,2 ; (a local energy minimum is defined as a state SL , at which any one-spin reversal increases the energy E );
- the global energy minimum E0 equals approximately: E0 = - 0,8 N .
Let's construct the spin-glass model of evolution [2]. We suppose, that an informational sequence (a genome of a model "organism") can be represented by a spin-glass system vector S . The evolved population is a set {Sk} of n sequences, k = 1,..., n. The selective values of model "organisms" Sk are defined as:
| f(Sk) = exp[- b E(Sk)] , | (4) |
where b is the selection intensity parameter.
The definition (4) implies that the model genome Sk consists of different elements Ski , which pairwise interact in accordance with the random interaction matrix Jij . In order to maximize the "organism" selective value (that is to minimize the energy E(S)), it is necessary to find a such combination of elements Si , that provides maximally cooperative interactions for given matrix Jij .
As in Quasispecies , we suppose, that 1) the evolution process consists of consequent generations, 2) new generations are obtained by selection (in accordance with selective values (4)) and mutations (sign reversals of sequence symbols, Ski --> - Ski , with the probability P for any symbol) of sequences Sk . The initial population is supposed to be random.
The described spin-glass model of evolution was analyzed by means of computer simulations and rough estimations [2]. The main evolution features are illustrated by Fig.1. Here n(E) is the number of sequences S , such that E(S) = E in a considered population; t is the generation number.
Fig. 1. The sequence distribution n(E) at different generations t ; t3 > t2 > t1 ; E0 and EL are global and local energy minima, respectively; the global energy minimum E0 equals approximately: E0 = - 0,8 N. Schematically, according to the computer simulations [2].
The spin-glass-type evolution is analogous to the Hamming distance case (see Quasispecies, Estimation of the evolution rate). But unlike the Hamming-distance model, the evolution converges to one of the local energy minima EL , which can be different for different evolution realizations.
Because one mutation gives the energy change dE ~ 2 (see (3)), and the typical time for one mutation per sequence dt is of the order (PN)-1, the total number of evolution generations T (at sufficiently large selection intensity b) can be estimated by the value T ~ (|E0|/dE)xdt ~ (0.8N /2)x(PN)-1. This value is close to the estimation of value T in the Hamming-distance case. So, the estimations of the evolution rate are roughly the same for both models, and we can use formulas (1)-(3) in Quasispecies to characterize the spin-glass-type evolution as well.
Analogously to the Hamming-distance case, we can consider the sequential method of energy minimization, that is the consequent changes of symbols (Si --> - Si) of one sequence and fixation only successful reversals. The sequential search needs smaller participant number than the evolution search. Nevertheless, the evolution search provides in average a more deep local energy minimum EL [2], because different valleys in energy landscape are looked through in evolution process simultaneously with descending to energy minima.
Thus, in the spin-glass case, the evolutionary search has a certain advantage with respect to the sequential search: it provides in average the greater selective value.
Conclusion. The spin-glass model of evolution refers to the "organisms", which have many randomly interacting genome elements. Evolution can be considered as a search of such genome elements, which are able to cooperate in the most successful manner.
References:
1. D.Sherrington , S.Kirkpatrick. // Physical Review Letters. 1975. V.35. N.26. P.1792. S.Kirkpatrick, D.Sherrington. // Physical Review B. 1978. V.17. N.11. P.4384.
2.V.G.Red'ko. Biofizika. 1990. Vol. 35. N.5. P. 831 (In Russian).
The hypercycle is a self-reproducing macromolecular system, in which RNAs and enzymes cooperate in the following manner (Fig.1): there are RNA matrices ( Ii ); i-th RNA codes i-th enzyme Ei (i = 1,2,...,n); the enzymes cyclically increase RNA's replication rates, namely, E1 increases replication rate of I2 , E2 increases replication rate of I3 , ..., En increases replication rate of I1 . In addition, the mentioned macromolecules cooperate to provide primitive translation abilities, so the information, coded in RNA-sequences, is translated into enzymes, analogously to the usual translation processes in biological objects. The cyclic organization of the hypercycle ensures its structure stability. For effective competition, the different hypercycles should be placed in separate compartments.
Fig. 1. Hypercycle structure. Ii are RNA matrices, Ei are replication enzymes (i = 1,2,...,n).
The replication enzymes ensure the more accurate RNAs' replication as compared with quasispecies, providing opportunities for further macromolecular structure improvements. M. Eigen and P. Schuster consider hypercycles as predecessors of protocells (primitive unicellular biological organisms) [1].
Let's review shortly the mathematical description of hypercycles, taking into account the original model [1] as well as the analysis by R.Feistel, Yu. M. Romanovskii, and V.A.Vasil'ev [2], who modeled a hypercycles competition in coacervate-type compartments.
We suppose, that 1) the hypercycles are placed into coacervates [3]; 2) each coacervate includes only one type of the hypercycles; 3) any coacervate volume is proportional to the number of macromolecules inside it; 4) a translation process is much quicker than a replication one (the latter means that it is sufficient to consider the RNAs dynamics only [1]). Using these assumptions, we obtain the following equations:
| dNi /dt = Vfi , | V = c-1 Si Ni , | xi = Ni /V , | i = 1,2,..., n, | (1) |
where Ni and xi are a number of molecules of i-th RNA and its concentration in a coacervate, respectively; V is a coacervate volume; c is a constant, characterizing a total concentration of macromolecules in a given coacervate; fi is a synthesis rate of i-th RNA. Values fi are defined as:
| fi = a xi xj , | i = 1,2,..., n, | j = i -1 + ndi1, | (2) |
where a is a synthesis rate parameter (for the sake of simplicity we assume the value a to be the same for all RNAs in a given hypercycle), dij is the Kronecker symbol (dij = 1, if j = i; dij = 0, otherwise). Eq. (2) takes into account the cyclic structure of hypercycles (see Fig.1). From (1) we obtain:
| dxi /dt = fi - xi c-1 Sj fj , | (3) |
| dV/dt = V c-1 Sj fj . | (4) |
According to (2),(3), the concentration dynamics in a particular hypercycle is described by the nonlinear ordinary differential equations, which were analyzed [1] by qualitative methods. The analysis showed, that if the number of hypercycle member n is less than or equal to 4, the macromolecules concentrations xi converge to the following equilibrium values:
| x0i = c /n, | (5a) |
and if n > 4 the concentrations xi converge to a stable limit cycle, that is a periodic orbit in the concentration hyperspace. For the limit cycles, the mean values of the macromolecules concentrations xi are determined by the same formula [1] :
| <xi > = c /n. | (5b) |
If several hypercycles have different replication abilities, their volumes increase with different rates. Averaging on periodic concentration oscillations (if needed), we can deduce, that according to (4), the hypercycle, having the greatest value
| Wk = < ck-1 Sj fkj > | (6) |
(k is the hypercycle type index), possesses the greatest selective ability.
In order to consider the hypercycles competition explicitly, let's suppose, that any coacervate splits into two parts, when its volume exceeds a certain critical value, and that the total volume of all types of hypercycles is restricted by some constant: Sk Vk = VT = const (Vk is the total volume of k-th type of hypercycles). Then instead of Eq. (4), we have:
| dVk/dt = Wk Vk - Vk [VT-1SkWkVk] . | (7) |
The selective values Wk can be calculated from (2), (3), (5), (6) [2]:
| Wk = ak ck /nk | (8) |
Eq. (7) is well known [1]; according to its solution, only the hypercycle, having the maximal selective value Wm = maxk {Wk}, survives during competition.
Conclusion. Developing the hypercycle model, M.Eigen and P.Schuster discussed the very profound and difficult problem: how could the real very complex translation mechanism and unique genetic code be created during macromolecular self-organizing process? The problem was not solved, but the plausible evolution steps were outlined and the corresponding well-defined mathematical model was developed.
References:
1. M.Eigen, P.Schuster. "The hypercycle: A principle of natural self-organization". Springer Verlag: Berlin etc. 1979.
2. R.Feistel, Yu. M. Romanovskii, and V.A.Vasil'ev. Biofizika. 1980. Vol. 25. N.5. P. 882. (In Russian).
3. A.I.Oparin. "The origin of life". New York, 1938. A.I.Oparin. "Genesis and evolutionary development of life". New York, 1968.
A syser includes a polynucleotide matrix I, a replication enzyme E1, a translation enzyme E2 , and optional proteins E3 , E4, ..., En (Fig. 1).
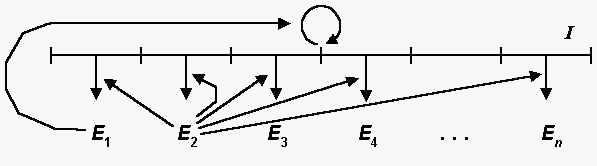
Fig 1. The general scheme of a syser. I is the polynucleotide matrix, E1 and E2 are the replication and the translation enzymes, respectively, E3 , E4, ..., En are optional proteins.
The polynucleotide matrix I codes proteins, the replication enzyme E1 provides the matrix replication process, the translation enzyme E2 provides the protein synthesis according to an information, stored in the matrix I . We can imply that there is the translation enzyme system (consisting of several enzymes) rather than the single translation enzyme - such a substitution does not change the mathematical description of sysers. The same is valid for the replication enzyme.
Whereas hypercycles [4] can be treated as a plausible model of the origin of translation mechanisms, sysers are more similar to real biological organisms than hypercycles. Nevertheless, possible scenarios of an origin of simple sysers from small molecules were also discussed [1,2]. Contrary to the hypercycle, the syser has a universal RNA replication enzyme. The mathematical analysis of sysers [3,5,6] is similar to that of hypercycles.
Analogously to hypercycles, different sysers should be placed into different compartments for effective competition. For example, we can model the sysers' competition, using the following assumptions [7]: 1) the different sysers are placed into separate coacervates [8], 2) any coacervate volume grows proportionally to the total macromolecules synthesis rate, 3) any coacervate splits into two parts when its volume exceeds a certain critical value. During a competition, a syser, having a maximal total macromolecules synthesis rate, is selected [3,5].
The model of sysers provides the ability to analyze evolutionary stages from a mini-syser, which contains only matrix I and replication E1 and translation E2 enzymes, to protocell, having rather real biological features. Some features can be modeled by assigning certain functions to optional proteins (Fig.1). For example, "Adaptive syser" [6] includes a simple molecular control system, which "turns on" and "turns off" synthesis of some enzyme in response to the external medium change; the scheme of this molecular regulation is similar to the classical model by F. Jacob and J. Monod [9]. The mathematical models of the adaptive syser as well as that of the mini-syser are described in the child node Adaptive syser: the model of hypothetical prebiological control system .
The scheme of sysers is similar to that of the self-reproducing automata by J. von Neumann [10]. The self-reproducing automata components and their syser's counterparts can be represented as follows:
|
|
|
|
|
|
|
|
|
|
Conclusion. Sysers is a rather universal model of self-reproducing system. It provides the ability to analyze evolutionary stages from a very simple macromolecular systems to protocells, having real biological features.
References:
1. V.A. Ratner and V.V. Shamin. In: Mathematical models of evolutionary genetics. Novosibirsk: ICG, 1980. P.66. V.A. Ratner and V.V. Shamin. Zhurnal Obshchei Biologii. 1983. Vol.44. N.1. PP. 51. (In Russian).
2. D.H. White. J. Mol. Evol. 1980. Vol.16. N.2. P.121.
3. R. Feistel. Studia biophysica.1983. Vol.93. N.2. P.113.
4. M. Eigen, P. Schuster. "The hypercycle: A principle of natural self-organization". Springer Verlag: Berlin etc. 1979.
5. V.G. Red'ko. Biofizika. 1986. Vol. 31. N.4. P. 701 (In Russian).
6. V.G. Red'ko. Biofizika. 1990. Vol. 35. N.6. P. 1007 (In Russian).
7. R. Feistel, Yu. M. Romanovskii, and V.A.Vasil'ev. Biofizika. 1980. Vol. 25. N.5. P. 882. (In Russian).
8. A.I. Oparin. "The origin of life". New York, 1938. A.I.Oparin. "Genesis and evolutionary development of life". New York, 1968.
9. F. Jacob and J. Monod. J. Mol. Biol. 1961. Vol. 3. P. 318.
10. J. von Neumann, A. W. Burks. "Theory of self-reproducing automata". Univ. of Illinois Press, Urbana IL, 1966.
| Synopsys: |
We describe here the model of an adaptive syser [1], which can modify its behavior in accordance with external environmental change. We consider also the mini-syser and compare selective abilities of both sysers.
The mini-syser (Fig. 1a) is a very simple syser, it includes only such macromolecules, which are necessary and sufficient for self-reproduction, namely, the matrix I , the replication enzyme E1 , and the translation enzyme E2 .
The adaptive syser (Fig. 1b) includes two additional enzymes: the regulatory enzyme E3 and the adapting enzyme (adapter) E4 . The regulatory enzyme E3 recognizes the environment state and "turns on" or "turns off" the synthesis of the adapter in accordance with the environment changes.
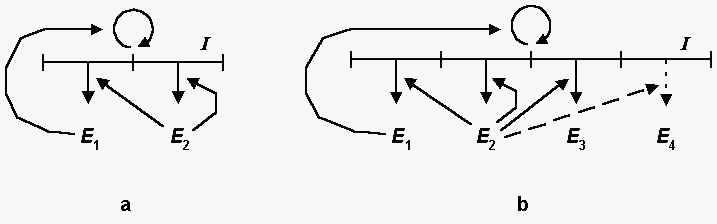
Fig 1. The schemes of mini-syser (a) and adaptive syser (b). I is the polynucleotide matrix, E1 , E2 , E3 , and E4 are replication, translation, regulatory, and adapting enzymes, respectively.
We suppose that there are two types of external environment, A and B. The environment A is a usual one, in which both sysers are able to reproduce themselves. The environment B is unusual, in which the macromolecular synthesis takes place only in the adaptive syser. The regulatory enzyme E3 in the adaptive syser is synthesized with a small rate in both A and B environments, it recognizes the environment state and "turns on" the synthesis of the adapter E4 in the environment B and "turns off" this synthesis in the environment A. The adapter E4 provides the macromolecular synthesis in the adaptive syser in the environment B.
For example, we may imply that the environment A corresponds to the usual syser's "food", usual powerful chemical substrate SA , and the environment B corresponds to the usually "uneatable" chemical substrate SB , which can be transformed into "eatable food" SA by means of the adapter E4. "For the sake of economy", it is natural to synthesize the adapter only then, when it is really needed, i.e. only in the environment B. To recognize the environment state, the regulatory enzyme E3, which is synthesized always, but "economically" (with a small rate), is included in the syser structure. The scheme of this molecular control is similar to the classical model by F. Jacob and J. Monod [2].
To describe quantitatively the syser's features, we use the following assumptions: 1) the different sysers are placed into separate coacervates; 2) any coacervate volume is proportional to the number of macromolecules inside it. From these assumptions we obtain the following equations:
| dNi /dt = Vfi , | V= c-1Si Ni , | xi = Ni /V , | (1) |
where Ni and xi are the number of molecules and the concentration of i-th macromolecules in a given coacervate, respectively; V is coacervate volume; fi is the synthesis rate i-th macromolecules; c is the constant total concentration of macromolecules in a coacervate (c = Si xi = const); here the index i = 0 refers to matrix I, and other i (= 1,2,3,4) refer i-th enzymes (E1 , E2 , E3 , E4), respectively. We define the synthesis rates as follows.
For the mini-syser we set:
| f0 = a0 x0 x1 , | fi = ai x0 x2 , | i = 1,2, | in environment A , | (2a) |
| f0 = f1= f2 = 0 , | in environment B . | (2b) |
For the adaptive syser we set:
| f0 = a0 x0 x1 , | fi = ai x0 x2 , | i = 1,2,3, | in environment A , | (3a) |
| f0 = b0 x0 x1 , | fi = bi x0 x2 , | i = 1,2,3,4, | in environment B . | (3b) |
Here ai and bi are synthesis rate parameters. Eqs. (2), (3) state that the matrix/enzyme synthesis rate is proportional to the matrix and replication/translation enzyme concentrations.
From (1) we obtain:
| dxi /dt = fi - xi c-1 Sj fj , | (4) |
| dV/dt = V c-1 Sj fj . | (5) |
According to (2) - (4), the concentration dynamics in a particular syser is described by nonlinear ordinary differential equations, which were analyzed [1] by usual qualitative methods. The analysis showed that the macromolecules concentrations xi converge to the equilibrium stable state x0 = {x0i }. In the environment A the values x0i are expressed as (for both sysers):
| x00 = c a0 a1 D , | x0i = c ai a2 D , | D = [a0a1 + a2 (a1+ ... + an)]-1, | i = 1, ..., n, | (6) |
where n is a number of enzymes in a considered syser (here we set a4 = 0) . For the adaptive syser in the environment B, the equilibrium concentrations x0i are also determined by Eq. (6) after substitution bi instead ai .
According to equation (5), the coacervate volume rates are proportional to selective values:
| W = c-1 Sj fj . | (7) |
Analogously to hypercycles, we can consider the competition of mini-syser and adaptive syser explicitly, supposing that the total coacervates volume for both types of sysers should be constant. During competition, a syser, having the maximal selective value W , is selected. Assuming small convergence time to the equilibrium state x0 and substituting values x0i , determined by formulas (6), into (7) , we obtain the selective values of the considered sysers. For the mini-syser we have
| WMini_A = c a0 a1 a2 [a0a1 + a2 (a1+ a2 )]-1 , | WMini_B = 0, | (8) |
in the environments A and B, respectively. For the adaptive syser the corresponding selective values are expressed as follows:
| WAdaptive_A
= c a0 a1 a2
[a0 a1+
a2 (a1+ a2
+ a3)]-1 , WAdaptive_B = c b0 b1 b2 [b0 b1 + b2 (b1+ b2 + b3 + b4)]-1 . |
(9) |
These expressions show, that in the environment A , the mini-syser has a selective advantage with respect to the adaptive one, because WMini_A is always greater, than WAdaptive_A . Such a disadvantage of the adaptive syser is due to the necessity to synthesize always the additional regulatory enzyme E3 . The disadvantage is small, if regulatory enzyme synthesis rate is small (a3 << a1, a2). Obviously, the adaptive syser is preferable in the environment B.
If the environment states (A and B) are intermittent, we can introduce the effective selective values of the considered sysers:
| WMini = (1 - PB) WMini_A , | (10) |
| WAdaptive = (1 - PB) WAdaptive_A + PB WAdaptive_B , | (11) |
where PB is the probability of the environment B . The adaptive syser has a selective advantage with respect to the mini-syser, if WAdaptive > WMini . From expressions (8)-(11) we can see that the adaptive syser is significantly preferable, if the regulatory enzyme synthesis rate is small (a3 << a1, a2) and the macromolecular synthesis rate in the environment B as well as the probability of this environment are sufficiently large (bi ~ ai and PB ~ 1).
Thus, the adaptive syser does have a selective advantage with respect to the mini-syser, however not always, but only if the "expenses", needed to support the molecular control system operation, are sufficiently small.
Conclusion. The control system of the adaptive syser could be the first control system, which was "invented" by biological evolution. The adaptive syser model demonstrates quantitatively, that the new evolutionary invention has selective advantages, if "invention profits" are greater than "invention expenses".
References:
1. V.G.Red'ko. Biofizika. 1990. Vol. 35. N.6. P. 1007 (In Russian).
2. F.Jacob and J.Monod. J. Mol. Biol. 1961. Vol. 3. P. 318.
The mathematical theory of population genetics describes quantitatively the gene distribution dynamics in evolving populations. The theory includes two main types of models: deterministic models (implying an infinitely large population size) and stochastic ones (finite population size). See Mathematical methods of population genetics for details.
Population genetics was intensively developed until the 1960s, when the difficulties of genetics became clear from molecular investigations.
As to the evolution aspects, the evolutionary rate of amino-acids substitutions as well as the protein polymorphism were estimated. In order to explain these experimental results, Motoo Kimura proposed the neutral theory of molecular evolution [1,2]. The main assumption of Kimura's theory is: the mutations at the molecular level (amino- and nuclear-acid substitutions) are mostly neutral or slightly disadvantageous (essentially disadvantageous mutations are also possible, but they are eliminated effectively from populations by selection). This assumption agrees with the mutational molecular substitution rate observed experimentally and with the fact that the rate of the substitutions for the less biologically important part of macromolecules is greater than for the active macromolecule centers.
Using mathematical methods of population genetics, M. Kimura deduced a lot of the neutral theory consequences, which are in rather good agreement with molecular genetics data [2].
The mathematical models of the neutral theory are essentially stochastic, that is, a relatively small population size plays an important role in the fixation of the neutral mutations.
If molecular substitutions are neutral, then why is progressive evolution possible? To answer this question, M.Kimura uses the concept of gene duplication developed by S.Ohno [3]. According to M.Kimura, gene duplications create unnecessary, surplus DNA sequences, which in turn drift further because of random mutations, providing the raw material for a creation of new, biologically significant genes.
The evolutionary concepts of the neutral theory came from interpretations of biological experiments; this theory was strongly empirically inspired. The other type of theory, a more abstract one, was proposed by Stuart A. Kauffman: NK automata or Boolean networks.
Theoretical population genetics and the neutral theory of molecular evolution describe the general features of genetic evolution. Nevertheless, these theories don’t consider the cybernetic properties of biological organisms. The theory of NK automata by S.A.Kauffman is a very interesting step towards understanding the evolution of the "program-like, computational" abilities of biological systems. This theory is mainly illustrative, however, it provides "a challenging scenario" (well developed mathematically) of the cybernetic evolution of the living cells.
References:
1. M. Kimura. Nature. London, 1968.V.217. PP.624.
2. M. Kimura. "The neutral theory of molecular evolution". Cambridge Un-ty Press. 1983.
3. S. Ohno. "Evolution by gene duplication". Berlin, Springer-Verlag, 1970.
| Pij = nij /n , | Pi = S j Pij , | Wi =Pi-1 S j Wij Pij , | (1) |
where n is the population size, index i refers to the class of organisms {Ai Aj}j=1,2,..., K , which contain the gene Ai. The population is supposed to be a panmictic4) one: during reproduction the new gene combinations are chosen randomly throughout in the whole population. For panmictic populations the Hardy-Weinberg principle can be approximately applied [1]:
| Pij =Pi Pj , | i, j = 1,...,K . | (2) |
Eqs. (2) implies, that during mating the genotypes are formed proportionally to the corresponding gene frequencies.
The evolutionary dynamics of the population in terms of the gene frequencies Pi can be described by the following differential equations [1,2,4]:
| dPi /dt = Wi Pi - <W> Pi - S j uji Pi + S j uij Pj , | i = 1,...,K , | (3) |
where t is time, <W> = S ij Wij Pij is the mean fitness in a population; uij is the mutation rate of the transition Aj --> Ai, uii =0 (i, j = 1,..., K). The first term in the right side of Eqs. (3) characterizes the selection of the organisms in accordance with their fitnesses, the second term takes into account the condition S i Pi = 1, the third and fourth terms describe the mutation transitions.
Note that similar equations are used in the quasispecies model (for the deterministic case) [5].
Neglecting the mutations, we can analyze the dynamics of genes in the population by means of the equations:
| dPi /dt = Wi Pi - <W> Pi , | i = 1,...,K . | (4) |
Using (1), (2), (4), one can deduce (under the condition that the values Wij are constant), that the rate of increase for the mean fitness is proportional to the fitness variance V = S i Pi ( Wi - <W>)2 [1,3]:
| d<W>/dt = 2 S i Pi ( Wi - <W>)2 . | (5) |
In accordance with (4), (5), the mean fitness <W> always increases, until an equilibrium state (dPi /dt = 0) is reached.
The equation (5) characterizes quantitatively The Fundamental Theorem of Natural Selection (R.A.Fisher, 1930), which in our case can be formulated as follows [3]:
In a sufficiently large panmictic population, where the organisms' fitness is determined by one locus and the selection pressure parameters are defined by the constant values Wij, the mean fitness in a population increases, reaching a stationary value in some genetic equilibrium state. The increase rate of the mean fitness is proportional to the fitness variance; it becomes zero in an equilibrium state.
The described model is a simple example of the deterministic approach. The wide spectrum of analogous models, which describe the different particularities, concerning several gene loci, age and female/male distributions in a population, inbreeding, migrations, subdivisions of populations, were developed and investigated, especially in connection with concrete genetic data interpretations [1,3,4].
Stochastic models
Deterministic models provide
effective methods for evolving population description. However,
they use the approximation of an infinitely large population size,
which is too strong for many real cases. To overcome this
limitation, the probabilistic methods of population genetics
were developed [1,3,4,6]. These methods include the analysis by
means of Markov chains (especially, by using the generating
functions) [4,7], and the diffuse approximation [1,3,4,6].
Below we sketch the main equations and some examples of the diffuse approximation. This approximation provides a non-trivial and effective method of population genetics.
We consider a population of diploid organisms with two alleles A1 and A2 in a certain locus. The population size n is supposed to be finite, but sufficiently large, so that the gene frequencies can be described by continuous values. We also suppose that the population size n is constant.
Let's introduce the function j = j (X,t|P,0) , which characterizes the probability density of the frequency X of the gene A1 at the time moment t under condition that the initial frequency (at t = 0) of this gene is equal to P. Under the assumption that the changes of the gene frequencies at one generation are small, the populations dynamics can be described approximately by the following partial differential equations [1,3,4]:
| ¶j/¶t = - ¶ (Md X j )/¶X + (1/2) ¶ 2(Vd X j )/¶X2 , | (6) |
| ¶j/¶t = Md P ¶j/¶P + (1/2)Vd P ¶ 2j/¶P2 , | (7) |
where Md X , Md P and Vd X , Vd P are the mean values and the variances of the changes of the frequencies X, P during one generation; time unit is equal to one generation. Eq. (6) is the forward Kolmogorov differential equation (in physics it is called the Fokker-Planck equation); Eq. (7) is the backward Kolmogorov differential equation.
The first terms in the right sides of Eqs. (6), (7) describe a systematic selection pressure, which is due to the fitness difference of the genes A1 and A2. The second terms characterize the random drift of the frequencies, which is due to the fluctuations in the finite size population.
Using Eq. (6), one can determine the time evolution of the gene frequency distribution, Eq. (7) provides the means to estimate the probabilities of gene fixation.
Assuming that 1) the fitnesses of gene A1 and A2 are equal to 1 and 1-s, respectively and 2) the gene contributions to the fitnesses of the gene pairs A1 A1, A1 A2, and A2 A2 are additive, one can obtain, that the values Md X , Md P and Vd X , Vd P are determined by the following expressions [1,3,4]:
| Md X = sX(1-X) , | Md P = sP(1-P) , | Vd X = X(1-X)/2n , | Vd P = P(1-P)/2n . | (8) |
If the evolution is purely neutral (s = 0), Eq. (6) takes the form:
| ¶j/¶t = (1/4n) ¶ 2[X(1-X)j]/¶X2 . | (9) |
This equation was solved analytically by M.Kimura [1,6]. The solution is rather complex. The main results can be summarized as follows: 1) only one gene (A1 or A2) is fixed in the final population, 2) the typical transition time from the initial gene frequency distribution to the final one is of the order of 2n generations. Note that these results agree with the results of a simple neutral evolution game.
Using Eq. (7), we can estimate the probability of the fixation of the gene A1 in the final population u(P). Considering the infinite time asymptotic, for the final population we can set ¶j/¶t = 0. The probability to be found can be approximated by the value [1]: u(P) = j/2n (here u(P) = j dX, where dX = 1/2n is the minimal frequency change step in population, see also [3] for more rigorous consideration). Using this approximation and combining (7), (8), we obtain:
| s du /dP + (1/4n) d2u /dP2 = 0 . | (10) |
Solving this simple equation for the natural boundary conditions: u (1) = 1, u (0) = 0, we obtain the probability of gene A1 fixation in a final population [1,3,6]:
| u(P) = [1 - exp (- 4nsP)] [1 - exp (- 4ns)]-1 . | (11) |
This expression shows, that if 4ns << 1, the neutral gene fixation takes place: u(P) » P, if 4ns >> 1, the advantageous gene A1 is selected: u(P) » 1; the population size nc ~ (4s)-1 is the boundary value, demarcating "neutral" and "selective" regions.
Conclusion
The mathematical models of population
genetics describe the gene frequency distributions in evolving
populations. The deterministic methods are used to analyze the
mean frequency dynamics; the stochastic methods take into account
the fluctuations, which are due to the finite population size.
Glossary:
1) Diploid organism: An individual having two chromosome sets in each of its cells.
2) Allele: One of the different forms of a gene that can exist at a single locus.
3) Gene locus: The specific place on a chromosome where a gene is located.
4) Panmictic population: Random-mating population.
References:
1. J.F. Crow, M. Kimura. "An introduction to population genetics theory". New York etc, Harper & Row. 1970.
2. T. Nagylaki. "Introduction to theoretical population genetics ". Berlin etc, Springer Verlag. 1992.
3. Yu.M. Svirezhev, V.P. Pasekov. "Fundamentals of mathematical evolutionary genetics". Moscow, Nauka. 1982 (In Russian), Dordrecht, Kluwer Academic Publishers, 1990.
4. P.A.P. Moran. "The statistical processes of evolutionary theory", Oxford, Clarendon Press, 1962.
5. M. Eigen. Naturwissenshaften. 1971. Vol.58. P. 465. M. Eigen, P. Schuster. "The hypercycle: A principle of natural self-organization". Berlin etc, Springer Verlag. 1979.
6. M. Kimura. "The neutral theory of molecular evolution". Cambridge Un-ty Press. 1983.
7. S. Karlin. "A first course in stochastic processes". New York, London, Academic Press. 1968.
An automaton operates in discrete time. The set of the output signals of the Boolean elements at a given moment of time characterizes a current state of an automaton. During an automaton operation, the sequence of states converges to a cyclic attractor. The states of an attractor can be considered as a "program" of an automaton operation. The number of attractors M and the typical attractor length L are important characteristics of NK automata.
The automaton behavior depends essentially on the connection degree K.
If K is large (K = N), the behavior is essentially stochastic. The successive states are random with respect to the preceding ones. The "programs" are very sensitive to minimal disturbances (a minimal disturbance is a change of an output of a particular element during an automaton operation) and to mutations (changes in Boolean element types and in network connections). The attractor lengths L are very large: L ~ 2N/2 . The number of attractors M is of the order of N. If the connection degree K is decreased, this stochastic type of behavior is still observed, until K ~ 2.
At K ~ 2 the network behavior changes drastically. The sensitivity to minimal disturbances is small. The mutations create typically only slight variations an automaton dynamics. Only some rare mutations evoke the radical, cascading changes in the automata "programs". The attractor length L and the number of attractors M are of the order of N1/2. This is the behavior at the edge of chaos, at the borderland between chaos and order.
The NK automata can be considered as a model of regulatory genetic systems of living cells. Indeed, if we consider any protein synthesis (gene expression) as regulated by other proteins, we can approximate a regulatory scheme of a particular gene expression by a Boolean element, so that a complete network of molecular-genetic regulations of a cell can be represented as a network of a NK automaton.
S.A.Kauffman argues that the case K ~ 2 is just appropriate to model the regulatory genetic systems of biological cellular organisms, especially in evolutionary context. The main points of this argumentation are as follows:
Because the regulatory structures at the edge of chaos (K ~ 2) ensure both stability and evolutionary improvements, they could provide the background conditions for an evolution of genetic cybernetic systems. That is, such systems have "the ability to evolve". So, it seems quite plausible, that such kind of regulatory genetic structures was selected at early stages of life, and this in turn made possible the further progressive evolution.
References
S. A. Kauffman. Scientific American. 1991. August. P. 64.
S. A. Kauffman. The Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, New York, 1993.S. A. Kauffman.At Home in the Universe: The Search for Laws of Self-Organization and Complexity, Oxford University Press, Oxford, 1995.
[Node to be completed]
| Synopsys: |
This principle is tautological in the sense that stability can be defined as that what does not (easily) change or disappear. Instability then is, by negation, that what tends to vanish or to be replaced by some other configuration, stable or unstable. The word "configuration" denotes any phenomenon that can be distinguished. It includes everything that is called feature, property, state, pattern, structure or system.
The principle can be interpreted as stating a basic distinction between stable configurations and configurations undergoing variation. This distinction has a role in evolution which is as fundamental as that between A and not A in logic. Without negation, we cannot have a system of logic. Without (in)stability we cannot describe evolution. The tautology plays a role similar to the principle of contradiction: "A and not A cannot both be true". The distinction between stable and changing is not as absolute as that between A and not A, though. We do not require a principle of the excluded middle, since it is clear that most configurations are neither absolutely stable nor absolutely unstable, but more or less stable. In this more general formulation, the principle would read:
More stable configurations are less easily eliminated than less stable ones
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
| Synopsys: |
This principle implies a fundamental asymmetry in evolution: one direction of change (from unstable to stable) is more likely than the opposite direction. The generalized, "continuous" version of the principle is the following:
The probability of transition from a less stable configuration A to a more stable one B is larger than the probability for the inverse transition: P (A -> B) > P (B -> A) (under the condition P (A -> B) =/ 0)
A similar principle was proposed by Ashby in his Principles of the Self-Organizing System (1962):"We start with the fact that systems in general go to equilibrium. Now most of a system's states are non-equilibrial [...] So in going from any state to one of the equilibria, the system is going from a larger number of states to a smaller. In this way, it is performing a selection, in the purely objective sense that it rejects some states, by leaving them, and retains some other state, by sticking to it. "
This reduction in the number of reachable states signifies that the variety, and hence the statistical entropy, of the system diminishes. It is because of this increase in neguentropy or organization that Ashby calls the process self-organization. But how does this fit in with the 2nd law of thermodynamics, which states that entropy in closed systems cannot decrease? The easy way out is to conclude that such a self-organizing system cannot be closed, and must lose entropy to its environment (von Foerster, 1960).
A deeper understanding can be reached by going back from the statistical definition of entropy to the thermodynamic one, in terms of energy or heat. Energy is defined as the capacity to do work, and working means making changes, that is to say exerting variation. Hence energy can ve viewed as potential variation. A stable configuration does not undergo variation. In order to destroy a stable equilibrium, you need to add energy, and the more stable the configuration, the more energy you will need. Therefore stability is traditionally equated with minimal energy.
The 1st law of thermodynamics states that energy is conserved. A naive interpretation of that law would conclude that the principle of asymmetric transitions cannot be valid, since it postulates a transition from an unstable (high energy) to a stable (low energy) configuration. If energy is absolutely conserved, then an unstable configuration can only be followed by another unstable configuration. This is the picture used in classical mechanics, where evolution is reversible, that is to say symmetric. Incidentally, this shows that the principle of asymmetric transitions is not tautological - though it may appear self-evident - , since a perfectly consistent theory (classical mechanics) can be built on its negation.
Thermodynamics has enlarged that picture by allowing energy dissipation. But what happens with the "dissipated" energy? A simple model is provided by a quantum system (e.g. an electron bound in an atom) with its set of - usually discrete - energy levels. A configuration at a higher level will spontaneously fall down to a lower level, emitting a photon which carries the surplus energy away. In order to bring back the electron to its higher level, energy must be added by having a photon of the right energy and direction hit the electron, a rather improbable event. Hence, the low level can be viewed as a stable configuration, with a small probability of transition.
The conjunction of energy conservation and asymmetric transitions implies that configurations will tend to dissipate energy (or heat) in order to move to a more stable state. For a closed system, this is equivalent to the thermodynamical interpretation of the 2nd law, but not to the statistical one, as the statistical entropy can decrease when transition probabilities are asymmetric. In an open system, on the other hand, where new energy is continuously added, the configuration will not be able to reach the minimum energy level. In that case we might assume that it will merely tend to maximally dissipate incoming energy, since transitions where energy is emitted are (much) more probable than transitions where energy is absorbed. That hypothesis seems equivalent to the Law of maximum entropy production (Swenson, 19), which describes dissipative structures and other far-from-equilibrium configurations. In such configurations the stability is dynamic, in the sense that what is maintained is not a static state but an invariant process.
Such an application of the principle of asymmetric transitions is opposite to the most common interpretation of the 2nd law, namely that disorder and with it homogeneity tend to increase. In the present view, configurations tend to become more and more stable, emitting energy in the process. This might be seen as a growing differentiation between the negative energy of stable bonds, and the positive energy of photons and movement. Recent cosmological theories hypothesize a similar spontaneous separation of negative and positive energies to account for the creation of the universe out of a zero-energy vacuum (Hawking, 1988).
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
One might object that this is not a good illustration of the process of evolution since there is an external force, gravity, which pulls the system in a determined direction, unlike most other evolutionary systems which undergo blind variation without any sense of direction. However, it is easy to devise systems that move in a specific direction because of asymmetric transitions, independently of, or even in spite of, forces pushing them in a different direction.
Imagine the following set-up (see fig.), where a ball is positioned on a surface that looks like a slightly skewed horizontal staircase. The vertical wall of the stair makes it impossible for the ball to move to the left. However, the ball needs just a small impulse to move over the gently inclining slope on the right and reach the next stair (B). In that next state, again moving back to the left is precluded, while continuing movement to the right (C) is relatively easy. Thus we have a system where P(A->B) >> P(B->A). We can imagine that if the whole set-up is gently shaken (in random directions, i.e. blind variation), the ball will move more and more to the right and never come back.
We could even imagine that the set-up as a whole is not horizontal but slightly inclined so that position B is elevated with respect to A, and C with respect to B, etc. In that case, the random moves would make the marble effectively move upwards, against the force of gravity. We could also imagine a "staircase" forming a loop so that position Z is identical to position A (as in a famous Escher drawing where figures are climbing up a staircase that turns back into itself). In that case, the marble will just continuously cycle along the staircase, like in a 1 dimensional attractor. With a two dimensional design, much more complex figures are possible, including fractal attractors.
An alternative set-up is one where it is not the environment (the staircase) that has an asymmetrical effect, but the system (marble) itself. For example, some seeds are shaped such that they can easily enter a tissue (or animal fur), but it is almost impossible to pull them back (see Fig.). The only way to get rid of them is by pulling them forward in the direction they originally entered.
"Fitness", the hypothesized quality distinguishing systems or states that are selected from those that are eliminated, can be reformulated as a general measure F for the likeliness that a particular configuration x will be reached in a stochastic process:
F (xi) = Sumj P(xj -> xi)
(i,j 
{1,...,n}, )
where P(xj -> xi) is the probability of the transition xj -> xi
High fitness (F > 1) of a state x means that on average more transitions enter x than leave x (the sum of all transition probabilities leaving x can never be >1). Thus, while the process runs, high fitness states will become more probable, and low fitness states less probable, as would be expected from a process undergoing natural selection.
A doubly stochastic process is defined by the requirement that F (xi) = 1 for all states xi. It can be shown that double stochasticity is a necessary and sufficient condition for a Markov process to be characterized by a non-decreasing statistical entropy function, i.e. a function of the probabilities which can only increase (or remain the same) over time, whatever the initial distribution of probabilities. Such processes correspond to the irreversible processes implied by the second law of thermodynamics. In a more general process, fitness can be larger or smaller for different states, and thus probability would tend to concentrate in the high fitness states, decreasing overall entropy. So, a necessary and sufficient condition for a Markov process to allow self-organization (i.e. decrease of statistical entropy) is that it have a non-trivial fitness function, i.e. there are x's such that F(x) =/ 1. Assuming classical probabilities, the sum of all P's must be 1 and thus we have the condition: Sumi F(xi) = n. Therefore, for every F(x) > 1, there must be at least one F(y) <1. This condition is equivalent to saying that selection is possible, because there are different fitness configurations from which to choose.
Having symmetric transition probabilities is a sufficient condition for a Markov process to be doubly stochastic. Indeed, symmetry means that P(xj -> xi) = P(xi -> xj) for all i,j and thus: 1 = Sumj P(xi -> xj) = Sumj P(xj -> xi) = F(xi).
Therefore, having asymmetric transition probabilities is a necessary condition for a Markov process to have non-trivial fitness, and thus, to allow self-organization.
We can also interpret the P's not as probabilities but as effective numbers or frequencies N (e.g. size of a population) which can be different from 1. In that case, the total number N = Sumi N(xi) can increase or decrease during the process, and we get a model that resembles population dynamics, where fitness gets its traditional meaning from biological evolution theory: F (x) = N(x(t)) / N(x(t-1)).
| Synopsys: |
This principle is not self-evident, but can be motivated by Ockham's razor. If it were not valid, we would have to introduce some explanation (e.g. design by God) to account for the "foreknowledge" of variation, and that would make the model more complicated than it needs to be. The blindness of variation is obvious in biological evolution, based on random mutations and recombinations. Yet even perfectly deterministic dynamical systems can be called blind, in the sense that if the system is complex enough it is impossible to predict whether the system will reach a particular attractor (select a stable configuration of states) without explicitly tracing its sequence of state transitions (variation) (Heylighen, 1991).
Of course many interactions are not blind. If I tackle a practical problem, I normally do not try out things at random, but rather have some expectations of what will work and what will not. Yet this knowledge itself was the result of previous trial-and-error processes, where the experience of success and failure was selectively retained in my memory, available for guiding later activities. Similarly, all knowledge can be reduced to inductive achievements based on blind-variation-and-selective-retention (BVSR) at an earlier stage. Together with Campbell (1974), I postulate that it must be possible to explain all cases of "non-blindness" (that is to say variation constrained in such a way as to make it more likely to satisfy selection) as the result of previous BVSR processes.
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
| Synopsys: |
Although this principle is again self-evident or tautologous, it leads to a number of useful and far from trivial conclusions. For example, the less numerous or the farther apart potential stable configurations are, the more variation (passing through a variety of configurations) the system will have to undergo in order to maintain its chances to find a stable configuration. In cases where selection criteria, determining which configurations are stable and which are not, can change, it is better to dispose of a large variety of possible configurations. If under a new selective regime configurations lose their stability, a large initial variety will make it probable that at least some configurations will retain their stability. A classic example is the danger of monoculture with genetically similar or identical plants: a single disease or parasite invasion can be sufficient to destroy all crops. If there is variety, on the other hand, there will always be some crops that survive the invasion.
Another special case is the "order from noise" principle (von Foerster, 1960), related to "order out of chaos". Noise or chaos can here be interpreted as rapid and blind variation. The principle states that addition of such noise makes it more likely for a system to evolve to an ordered (stable) configuration. A practical application is the technique of (simulated) annealing, where noise or variation is applied in stepwise decreasing amounts, in order to reach a maximally stable configuration.
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
| Synopsys: |
The stable configurations resulting from BVSR processes can be seen as primitive elements: their stability distinguishes them from their variable background, and this distinction, defining a "boundary", is itself stable. The relations between these elements, extending outside the boundaries, will initially still undergo variation. A change of these relations can be interpreted as a recombination of the elements. Of all the different combinations of elements, some will be more stable, and hence will be selectively retained.
Such a higher-order configuration might now be called a system. The lower-level elements in this process play the role of building blocks: their stability provides the firmness needed to support the construction, while their variable connections allow several configurations to be tried out. The principle of "the whole is more than the sum of its parts" is implied by this systemic construction principle, since the system in the present conception is more than a mere configuration of parts, it is a stable configuration, and this entails a number of emergent constraints and properties (Heylighen, 1991). A stable system can now again function as a building block, and combine with other building blocks to a form an assembly of an even higher order, in a recursive way.
Simon (1962) has argued in his famous "The Architecture of Complexity" that such stable assemblies will tend to contain a relatively small number of building blocks, since the larger a specific assembly, the less probable that it would arise through blind variation. This leads to a hierarchical architecture, that can be represented by a tree.
Two extensions must be made to the Simon argument (cf. Heylighen, 1989). 1) If one takes into account autocatalytic growth, as when a small stable assembly makes it easier for other building blocks to join the assembly, the number of building blocks at a given level can become unlimited. 2) It is possible, though less probable, that a given building block would participate in several, overlapping stable assemblies; it suffices that its configuration would satisfy two (or more) selection criteria, determining stable systems. It is clear, however, that the more selection criteria a configuration would have to satisfy, the less likely that such a configuration would be discovered by blind variation. These two points lead us to generalize the tree structure of Simon's "nearly-decomposable" architecture to a loose or quasi-hierarchy (Joslyn, 1991), which in parts can be very flat, and where some nodes might have more than one mother node.
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
| Synopsys: |
This principle was proposed by the evolutionary biologist L. van Valen (1973), and is based on the observation to Alice by the Red Queen in Lewis Carroll's "Through the Looking Glass" that "in this place it takes all the running you can do, to keep in the same place."
Since every improvement in one species will lead to a selective advantage for that species, variation will normally continuously lead to increases in fitness in one species or another. However, since in general different species are coevolving, improvement in one species implies that it will get a competitive advantage on the other species, and thus be able to capture a larger share of the resources available to all. This means that fitness increase in one evolutionary system will tend to lead to fitness decrease in another system. The only way that a species involved in a competition can maintain its fitness relative to the others is by in turn improving its design.
The most obvious example of this effect are the "arms races" between predators and prey, where the only way predators can compensate for a better defense by the prey (e.g. rabbits running faster) is by developing a better offense (e.g. foxes running faster). In this case we might consider the relative improvements (running faster) to be also absolute improvements in fitness.
However, the example of trees shows that in some cases the net effect of an "arms race" may also be an absolute decrease in fitness. Trees in a forest are normally competing for access to sunlight. If one tree grows a little bit taller than its neighbours it can capture part of their sunlight. This forces the other trees in turn to grow taller, in order not to be overshadowed. The net effect is that all trees tend to become taller and taller, yet still gather on average just the same amount of sunlight, while spending much more resources in order to sustain their increased height. This is an example of the problem of suboptimization: optimizing access to sunlight for each individual tree does not lead to optimal performance for the forest as a whole.
In sum, in a competitive world, relative progress ("running") is necessary just for maintenance ("staying put").
In its emphasis on the stress that necessarily accompanies evolutionary development, the Red Queen Principle is related to the generalized "Peter Principle".
| Synopsys: |
The Peter Principle was first introduced by L. Peter in a humoristic book (of the same title) describing the pitfalls of bureaucratic organization. The original principle states that in a hierarchically structured administration, people tend to be promoted up to their "level of incompetence". The principle is based on the observation that in such an organization new employees typically start in the lower ranks, but when they prove to be competent in the task to which they are assigned, they get promoted to a higher rank. This process of climbing up the hierarchical ladder can go on indefinitely, until the employee reaches a position where he or she is no longer competent. At that moment the process typically stops, since the established rules of bureacracies make that it is very difficult to "demote" someone to a lower rank, even if that person would be much better fitted and more happy in that lower position. The net result is that most of the higher levels of a bureaucracy will be filled by incompetent people, who got there because they were quite good at doing a different (and usually, but not always, easier) task than the one they are expected to do.
The evolutionary generalization of the principle is less pessimistic in its implications, since evolution lacks the bureaucratic inertia that pushes and maintains people in an unfit position. But what will certainly remain is that systems confronted by evolutionary problems will quickly tackle the easy ones, but tend to get stuck in the difficult ones. The better (more fit, smarter, more competent, more adaptive) a system is, the more quickly it will solve all the easy problems, but the more difficult the problem will be it finally gets stuck in. Getting stuck here does not mean "being unfit", it just means having reached the limit of one's competence, and thus having great difficulty advancing further. This explains why even the most complex and adaptive species (such as ourselves, humans) are always still "struggling for survival" in their niches as energetically as are the most primitive organisms such as bacteria. If ever a species would get control over all its evolutionary problems, then the "Red Queen Principle" would make sure that new, more complex problems would arise, so that the species would continue to balance on the border of its domain of incompetence. In conclusion, the generalized Peter principle states that in evolution systems tend to develop up to the limit of their adaptive competence.
| Synopsys: |
At least since the days of Darwin, evolution has been associated with the increase of complexity: if we go back in time we see originally only simple systems (elementary particles, atoms, molecules, unicellular organisms) while more and more complex systems appear in later stages. However, from the point of view of classical evolutionary theory there is no a priori reason why more complicated systems would be preferred by natural selection. Evolution tends to increase fitness, but fitness can be achieved as well by very complex as by very simple systems. For example, according to some theories, viruses, the simplest of living systems, are degenerated forms of what were initially much more complex organisms. Since viruses live as parasites, using the host organisms as an environment that provides all the resources they need to reproduce themselves, maintaining a metabolism and reproductory systems of their own is just a waste of resources. Eventually, natural selection will eliminate all superfluous structures, and thus partially decrease complexity.
Ashby's Law of Requisite Variety states that in order to achieve complete control, the variety of actions a control system should be able to execute must be at least as great as the variety of environmental perturbations that need to be compensated. Evolutionary systems (organisms, societies, self-organizing processes, ...) obviously would be fitter if they would have greater control over their environments, because that would make it easier for them to survive and reproduce. Thus, evolution through natural selection would tend to increase control, and therefore internal variety. Since we may assume that the environment as a whole has always more variety than the system itself, the evolving system would never be able to achieve complete control, but it would at least be able to gather sufficient variety to more or less control its most direct neighbourhood. We might imagine a continuing process where the variety of an evolving system A slowly increases towards but never actually matches the infinite variety of the environment.
However, according to the complementary principles of selective variety and of requisite constraint, Ashby's law should be restricted in its scope: at a certain point further increases in variety diminish rather than increase the control that system A has over its environment. A will asymptotically reach a trade-off point, depending on the variety of perturbations in its environment, where requisite variety is in balance with requisite constraint. For viruses, the balance point will be characterised by a very low variety, for human beings by a very high one.
This analysis assumes that the environment is stable and a priori given. However, the environment of A itself consists of evolutionary systems (say B, C, D...), which are in general undergoing the same asymptotic increase of variety towards their trade-off points. Since B is in the environment of A, and A in the environment of B, the increase in variety in the one will create a higher need (trade-off point) in variety for the other, since it will now need to control a more complex environment. Thus, instead of an increase in complexity characterised by an asymptotic slowing down, we get a positive feedback process, where the increase in variety in one system creates a stronger need for variety increase in the other. The net result is that many evolutionary systems that are in direct interaction with each other will tend to grow more complex, and this with an ever increasing speed.
As an example, in our present society, individuals and organizations tend to gather more knowledge and more resources, increasing the range of actions they can take, since this will allow them to cope better with the possible problems appearing in their environment. However, if the people you cooperate or compete with (e.g. colleagues) become more knowledgeable and resourceful, you too will have to become more knowledgeable and resourceful in order to respond to the challenges they pose to you. The result is an ever faster race towards more knowledge and better tools, creating the "information explosion" we all know so well.
The present argument does not imply that all evolutionary systems will increase in complexity: those (like viruses, snails or mosses) that have reached a good trade-off point and are not confronted by an environment putting more complex demands on them will maintain their present level of complexity. But it suffices that some systems in the larger ecosystem are involved in the complexity race to see an overall increase of available complexity.
Now, it is well-documented by ecologists and evolutionary biologists that ecosystems tend to become more complex: the number of different species increases, and the number of dependencies and other linkages between species increases. This has been observed as well over the geological history of the earth, as in specific cases such as island ecologies which initially contained very few species, but where more and more species arose by immigration or by differentiation of a single species specializing on different niches (like the famous Darwin's finches on the Galapagos islands).
As is well explained by E.O. Wilson in his "The Diversity of Life", not only do ecosystems contain typically lots of niches that will eventually be filled by new species, there is a self-reinforcing tendency to create new niches. Indeed, a hypothetical new species (let's call them "bovers") occupying a hitherto empty niche, by its mere presence creates a set of new niches. Different other species can now specialize in somehow using the resources produced by that new species, e.g. as parasites that suck the bover's blood or live in its intestines, as predators that catch and eat bovers, as plants that grow on the bovers excrements, as furrowers that use abandoned bover holes, etc. etc. Each of those new species again creates new niches, that can give rise to even further species, and so on, ad infinitum. These species all depend on each other: take the bovers away and dozens of other species may go extinct.
This principle is not limited to ecosystems or biological species: if in a global system (e.g. the inside of a star, the primordial soup containing different interacting chemicals, ...) a stable system of a new type appears through evolution (e.g. a new element in a star, or new chemical compound), this will in general create a new environment or selector. This means that different variations will either be adapted to the new system (and thus be selected) or not (and thus be eliminated). Elimination of unfit systems may decrease complexity, selection of fit systems is an opportunity for increasing complexity, since it makes it possible for systems to appear which were not able to survive before. For example, the appearance of a new species creates an opportunity for the appearance of species-specific parasites or predators, but it may also cause the extinction of less fit competitors or prey.
However, in general the power for elimination of other systems will be limited in space, since the new system cannot immediately occupy all possible places where other systems exist. E.g. the appearance of a particular molecule in a pool of "primordial soup" will not affect the survival of molecules in other pools. So, though some systems in the neighbourhood of the new system may be eliminated, in general not all systems of that kind will disappear. The power for facilitating the appearance of new systems will similarly be limited to a neighbourhood, but that does not change the fact that it increases the overall variety of systems existing in the global system. The net effect is the creation of a number of new local environments or neighbourhoods containing different types of systems, while other parts of the environment stay unchanged. The environment as a whole becomes more differentiated and, hence, increases its complexity.
See also:
Heylighen F. (1996): "The Growth of Structural and Functional Complexity during Evolution", in: F. Heylighen & D. Aerts (eds.) (1996): "The Evolution of Complexity" (Kluwer, Dordrecht). (in press)
T.S. Ray: An evolutionary approach to synthetic biology
Dam McShea and the great chain of Being: does evolution lead to complexity?
W. Brian Arthur: "Why Do Things Become More Complex?", Scientific American, May 1993
PRNCYB-L discussion on Requisite Variety, Complexity & the edge of Chaos
| Synopsys: |
A fundamental criticism of the idea of increasing complexity, formulated among others by Stephen Jay Gould (1994), is that such an increase implies a preferred direction for evolution, a continuing "progress" or advance towards more sophisticated forms. Recent advances in evolutionary theory (such as the theory of punctuated equilibrium) and observation of evolutionary phenomena seem to indicate that evolution is a largely unpredictable, chaotic and contingent series of events, where small fluctuations may lead to major catastrophes that change the future course of development. At first sight, this seems inconsistent with any constant "direction". Yet, an example will show that there is no necessary contradiction.
Consider a rock that rolls down from the top of a steep mountain. Given that the slightest irregularity in the terrain may be sufficient to make the rock fall either into the one or the other of a host of downward slopes or valleys, the exact path of the rock will be virtually impossible to predict. Repeated experiments are likely to produce final resting positions that are miles apart. Yet, one thing will be certain: the final position will be lower than the initial position at the top. Although we cannot know the direction of movement in the horizontal dimensions, we do know that there is only one possible sense in which it can move along the vertical dimension: downward.
To apply this metaphor to evolution, we need to discover the equivalent of the "vertical" dimension, in other words we need to define a variable that can only increase during evolution (like vertical distance from the top). Entropy plays the role of such a variable for thermodynamic systems, but this seems hardly useful to describe complexification. Fisher's (1958) fundamental theorem of natural selection has shown that another such variable exists for populations of living systems: average fitness. This follows straightforwardly from the fact that fit individuals by definition will become more numerous, while the proportion of less fit individuals will decrease. This reasoning can be generalized to cover non-biological systems too (cf. the principle of asymmetric transitions).
It might be objected that fitness is a relative notion: what is fit in one type of environment may no longer be fit in another environment. Thus, the inexorable increase of fitness only holds in invariant environments (which seem wholly atypical if one takes into account co-evolution). Gould proposes the following example: the evolution from hairless elephant to woolly mammoth is due merely to a cooling down of the climate. If the climate becomes warmer again the woolly variant will lose its fitness relative to the hairless one, and the trend will be reversed.
Yet, there are ways to increase "absolute" fitness. First, the system may increase its internal or intrinsic fitness, by adding or strenghtening bonds or linkages between its components. This is typically accompanied by the increase of structural complexity. Second, the system may increase its fitness relative to its environment by increasing the variety of environmental perturbations that it can cope with, and thus its functional complexity.
This may be illustrated through the climate change example: though the warm-blooded, woolly mammoth is only relatively fitter than its hairless cousin, it is absolutely fitter than a cold-blooded reptile, which would never have been able to adapt to a cold climate, with or without hair. Warm-bloodedness means temperature control, i.e. the capacity to internally compensate a variety of fluctuations in outside temperature. The appearance of control is the essence of a metasystem transition, which can be seen as a discrete unit of evolutionary progress towards higher functional complexity.
All other things being equal, a system that can survive situations A, B and C, is absolutely fitter than a system that can only survive A and B. Such an increase in absolute fitness is necessarily accompanied by an increase in functional complexity. Thus, evolution will tend to irreversibly produce increases of functional complexity.
This preferred direction must not be mistaken for a preordained course that evolution has to follow. Though systems can be absolutely ordered by their functional complexity, the resulting relation is not a linear order but a partial order: in general, it is not possible to determine which of two arbitrarily chosen systems is most functionally complex. For example, there is no absolute way in which one can decide whether a system that can survive situations A, B and C is more or less complex or fit than a system that can survive C, D and E. Yet, one can state that both systems are absolutely less fit than a system that can survive all A, B, C, D and E. Mathematically, such a partial order can be defined by the inclusion relation operating on the set of all sets of situations or perturbations that the system can survive. This also implies that there are many, mutually incomparable ways in which a system can increase its absolute fitness. For example, the first mentioned system might add either D or E to the set of situations it can cope with. The number of possibilities is infinite. This leaves evolution wholly unpredictable and open-ended.
For example, though humans are in all likeliness absolutely more functionally complex than snails or frogs, evolution might well have produced a species that is very different from humans, yet is similarly at a much higher functional complexity level compared to the other species. In perhaps slightly different circumstances, the Earth might have seen the emergence of a civilisation of intelligent dogs, dolphins or octopuses. It is likely that analogous evolutions are taking place or have taken place on other planets. Though humanity seems to have reached the highest level of functional complexity in the part of evolution that we know, more intelligent and complex species may well exist elsewhere in the universe, or may appear after us on Earth. The conclusion is that a preferred direction for evolution in the present, generalized sense does not in any way support the ideology of anthropocentrism.
References:
| Synopsys: |
In the important characterizing sources (Laszlo, l987; Csanyi, l989 see also Goonatilake, l99l) these have been restricted to living and linguistic systems (focusing on genetic information and its consequences) but the work of, e.g., Prigogine's school on dissipative structures, opens up the high probability that minimally some abiotic systems are also "evolutionary". Unless this is so the origin of life will remain an unapproachable puzzle.
Mainstream synthetic evolutionary theory from biology (neodarwinan population biology) has had little impact here , although it could be said that most workers involved accept natural selection as being involved in greater or lesser degree, at one or more scalar levels; the field, however, does not appear in most hands to be driven by this concept. This is especially so because most studies focus on the regularities of change (what darwinians might term ' evolutionary trends', which for them are extremely problematic and always require careful qualification so as to avoid "teleology").
Here we uncover an important difference between standard darwinian thought and that in evolutionary systems. The former is resolutely mechanistic, while most versions of the latter, more or less explicitly, tentatively at least, reject mechanistic materialism as their basic philosophy. On this score we find interest in ideas like self-organization, autopoiesis, autogenesis, autocatakinesis, autognosis, semiosis and other ideas linked to change being generated from within a changing system rather than from outside in newtonian/darwinian style, and to the necessity for bringing the subjective observer explicitly into representations.
(2) agreeing on working definitions of basic terms: e.g., evolution, self-organization, development, emergence
(3) comparisons of currently competing concepts - autopoiesis, autogenesis, autocatakinesis, etc.
(4) how to formalize non-mechanistic systems
(5) the role of semiosis in natural science
(6) seeking the appropriate role of natural selection in evolutionary systems
(7) The problems of self-referential systems
(8) the problem of subjectivity in science
(9) reviewing again the ever present confusions about thermodynamics, as well as its role in evolutionary systems
References:
Csanyi, V., l989. Evolutionary Systems and Society: a General Theory. Duke University Press.
Goonatilake, S., l99l. The Evolution of Information: Lineages in Gene, Culture and Artefact. Pinter Publishers.
Laszlo, E., l987. Evolution: the Grand Synthesis. Shambala.
| Synopsys: |
Cybernetics, deriving from the Greek word for steersman (kybernetes), was first introduced by the mathematician Wiener, as the science of communication and control in the animal and the machine (to which we now might add: in society and in individual human beings). It grew out of Shannon's information theory, which was designed to optimize the transmission of information through communication channels, and the feedback concept used in engineering control systems. In its present incarnation of "second-order cybernetics", its emphasis is on how observers construct models of the systems with which they interact (see constructivism).
The main emphasis of cybernetics is on the circular mechanisms that allow complex systems to maintain, adapt, and self-organize. Such circularity or self-reference makes it possible to make precise, scientific models of purposeful activity, that is, behavior that is oriented towards a goal or preferred condition. In that sense, cybernetics proposes a revolution with respect to the linear, mechanistic models of traditional Newtonian science. In classical science, every process is determined solely by its cause, that is, a factor residing in the past. However, the behavior of living organisms is typically teleonomic, that is, oriented towards a future state, which does not exist as yet.
Cybernetics has discovered that teleonomy (or finality) and causality can be reconciled by using non-linear, circular mechanisms, where the cause equals the effect. The simplest example of such a circular mechanism is feedback. The simplest application of negative feedback for self-maintenance is homeostasis. The non-linear interaction between the homeostatic or goal-directed system and its environment results in a relation of control of the system over the perturbations coming from the environment.
See also: What are Cybernetics and Systems Science?
de Rosnay | Synopsys: |
A person threatened by the environment (or informed of an approaching pleasure or danger) prepares for action. The body mobilizes reserves of energy and produces certain hormones such as adrenalin, which prepare it for conflict or flight. This mobilisation can be seen in familiar physiological reactions. In the presence of emotion, danger, or physical effort the heart beats faster and respiration quickens. The face turns red or pales and the body perspires. The individual may experience shortness of breath, cold sweats, shivering, trembling legs. These physiological manifestations reflect the efforts of the body to maintain its internal equilibrium. Action can be voluntary--to drink when one is thirsty, to eat when hungry, to put on clothing when cold, to open a window when one is too warm--or involuntary--shivering, sweating.
The internal equilibrium of the body, the ultimate gauge of its proper functioning, involves the maintenance of a constant rate of concentration in the blood of certain molecules and ions that are essential to life and the maintenance at specified levels of other physical parameters such as temperature. This is accomplished in spite of modifications of the environment.
This extraordinary property of the body has intrigued many physiologists. In 1865 Claude Bernard noticed, in his Introduction to Experimental Medicine. that the "constancy of the internal milieu was the essential condition to a free life." But it was necessary to find a concept that would make it possible to link together the mechanisms that effected the regulation of the body. The credit for this concept goes to the American physiologist Walter Cannon. In 1932, impressed by "the wisdom of the body" capable of guaranteeing with such efficiency the control of the physiological equilibrium, Cannon coined the word homeostasis from two Greek words meaning to remain the same. Since then the concept of homeostasy has had a central position in the field of cybernetics.
Homeostasis is one of the most remarkable and most typical properties of highly complex open systems. A homeostatic system (an industrial firm, a large organization, a cell) is an open system that maintains its structure and functions by means of a multiplicity of dynamic equilibriums rigorously controlled by interdependent regulation mechanisms. Such a system reacts to every change in the environment, or to every random disturbance, through a series of modifications of equal size and opposite direction to those that created the disturbance. The goal of these modifications is to maintain the internal balances.
Ecological, biological, and social systems are homeostatic. They oppose change with every means at their disposal. If the system does not succeed in reestablishing its equilibriums, it enters into another mode of behavior, one with constraints often more severe than the previous ones. This mode can lead to the destruction of the system if the disturbances persist.
Complex systems must have homeostasis to maintain stability and to survive. At the same time it bestows on the systems very special properties. Homeostatic systems are ultrastable; everything in their internal, structural, and functional organization contributes to the maintenance of the same organization. Their behavior is unpredictable; "counterintuitive" according to Jay Forrester, or contravariant: when one expects a determined reaction as the result of a precise action, a completely unexpected and often contrary action occurs instead. These are the gambles of interdependence and homeostasis; statesmen, business leaders, and sociologists know the effects only too well.
For a complex system, to endure is not enough; it must adapt itself to modifications of the environment and it must evolve. Otherwise outside forces will soon disorganize and destroy it. The paradoxical situation that confronts all those responsible for the maintenance and evolution of a complex system, whether the system be a state, a large organization, or an industry, can be expressed in the simple question, How can a stable organization whose goal is to maintain itself and endure be able to change and evolve?
The heart of the Principia Cybernetica Project lies therefore in the establishment of a set of clear and coherent Principles of Cybernetics. As Principles, they should have the following properties:
The preliminary set of principles we propose are based on and expressed in terms of a set of primitive concepts of systems and cybernetics. Some of the principles have a long and venerable tradition in Cybernetics and Systems Science, while others are novel to Metasystem Transition Theory. Our analysis will on the one hand critically assess existing principles, clarifying their meaning, on the other hand try to formulate new principles which may generalize or interconnect known laws.
The ultimate goal is to arrive at a network of concepts and principles similar to a formal system, with "axioms" implicitly defining primitive concepts, definitions of higher order concepts, and "theorems", derived from the more primitive axioms and definitions. The fundamental principles, like all good axioms, are supposed to be self-evident. Their implications, like most theorems, on the other hand, may be far from trivial, and sometimes even counter-intuitive.
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
| Synopsys: |
Occam's razor is a logical principle attributed to the mediaeval philosopher (William of Occam (or Ockham). The principle states that one should not make more assumptions than the minimum needed. This principle is often called the principle of parsimony. It underlies all scientific modelling and theory building. It admonishes us to choose from a set of otherwise equivalent models of a given phenomenon the simplest one. In any given model, Occam's razor helps us to "cut away" those concepts, variables or constructs that are not really needed to explain the phenomenon. By doing that, developing the model will become much easier, and there is less chance of introducing inconsistencies, ambiguities and redundancies.
Though the principle may seem rather trivial, it is essential for model building because of what is known as the "underdetermination of theories by data". For a given set of observations or data, there is always an infinite number of possible models explaining those same data. This is because a model normally represents an infinite number of possible cases, of which the observed cases are only a finite subset. The non-observed cases are inferred by postulating general rules covering both actual and potential observations.
For example, through two data points in a diagram you can always draw a straight line, and induce that all further observations will lie on that line. However, you could also draw an infinite variety of the most complicated curves passing through those same two points, and these curves would fit the empirical data just as well. Only Occam's razor would in this case guide you in choosing the "straight" (i.e. linear) relation as best candidate model. A similar reasoning can be made for n data points lying in any kind of distribution.
Occam's razor is especially important for universal models such as the ones developed in General Systems Theory, mathematics or philosophy, because there the subject domain is of an unlimited complexity. If one starts with too complicated foundations for a theory that potentially encompasses the universe, the chances of getting any manageable model are very slim indeed. Moreover, the principle is sometimes the only remaining guideline when entering domains of such a high level of abstraction that no concrete tests or observations can decide between rival models. In mathematical modelling of systems, the principle can be made more concrete in the form of the principle of uncertainty maximization: from your data, induce that model which minimizes the number of additional assumptions.
This principle is part of epistemology, and can be motivated by the requirement of maximal simplicity of cognitive models. However, its significance might be extended to metaphysics if it is interpreted as saying that simpler models are more likely to be correct than complex ones, in other words, that "nature" prefers simplicity.
See also Occam's Razor:
as part of the scientific method in the sci.skeptic FAQ.
in the Encyclopedia Britannica
in the Physics FAQ
| Synopsys: |
This principle was probably first formulated by the philosopher and mathematician Gottfried Wilhelm Leibniz (a precursor of cybernetics and artificial intelligence, with his "calculus of thought") in the Monadology. It can be derived from the principle of Occam's razor, which implies that if there is no reason why two things should be distinguished then it is better to just identify them, so that one entity is left rather than two.
A similar idea underlies the Pauli Exclusion Principle in quantum physics, which states that no two particles ("fermions") can be in the same state at the same moment (otherwise, they would be indistinguishable and therefore there would be only a single particle). A more modern, cybernetic formulation, used by Gregory Bateson, is that of "a difference that makes a difference": distinctions are only useful insofar that they lead to further distinctions. If the initial distinction does not allow you to make any further distinctions, you should better drop it. This "relational" interpretation where the value of a distinctions depends on the further distinctions it is connected with can be formalized as the "bootstrapping axiom". It also underlies the microscopic interpretation of the principle of causality (identic causes have identic results), and a generalized version of empiricism, which says that postulated entities in a theory should (directly or indirectly) lead to observable differences.
| Synopsys: |
This is how Donald T. Campbell (1974) originally formulated the principle of downward causation. Let us try to clarify what this means. Reductionism can be defined as the belief that the behavior of a whole or system is completely determined by the behavior of the parts, elements or subsystems. In other words, if you know the laws governing the behavior of the parts, you should be able to deduce the laws governing the behavior of the whole.
Systems theory has always taken an anti-reductionist stance, noting that the whole is more than the sum of the parts. In other words, the whole has "emergent properties" which cannot be reduced to properties of the parts. Since emergence is a rather slippery concept, which has been defined in many different ways, most of which are highly ambiguous or fuzzy, I prefer to express this idea with the more precise concept of downward causation.
Downward causation can be defined as a converse of the reductionist principle above: the behavior of the parts (down) is determined by the behavior of the whole (up), so determination moves downward instead of upward. The difference is that determination is not complete. This makes it possible to formulate a clear systemic stance, without lapsing into either the extremes of reductionism or of holism:
| the whole is to some degree constrained by the parts (upward causation), but at the same time the parts are to some degree constrained by the whole (downward causation). |
Let me illustrate this with an example. It is well-known that snow crystals have a strict 6-fold symmetry, but at the same time that each crystal has a unique symmetric shape. The symmetry of the crystal (whole) is clearly determined by the physico-chemical properties of the water molecules which constitute it. But on the other hand, the shape of the complete crystal is not determined by the molecules. Once a shape has been formed, though, the molecules in the crystal are constrained: they can only be present at particular places allowed in the symmetric crystalline shape. The whole (crystal) constrains or "causes" the positions of the parts (molecules).
The appearance of this "two way causation" can be explained in the following way. Imagine a complex dynamic system. The trajectories of the system through its state space are constrained by the "laws" of the dynamics. These dynamics in general determine a set of "attractors": regions in the state space the system can enter but not leave. However, the initial state of the system, and thus the attractor the system will eventually reach is not determined. The smallest fluctuations can push the system either in the one attractor regime or the other. However, once an attractor is reached, the system loses its freedom to go outside the attractor, and its state is strongly constrained.
Now equate the dynamics with the rules governing the molecules, and the attractor with the eventual crystal shape. The dynamics to some degree determines the possible attractors (e.g. you cannot have a crystal with a 7-fold symmetry), but which attractor will be eventually reached is totally unpredictable from the point of view of the molecules. It rather depends on uncontrollable outside influences. But once the attractor is reached, it strictly governs the further movement of the molecules.
The same principle applies to less rigid, mechanistic systems such as living organisms. You cannot have organisms whose internal functioning flouts the rules of physics and chemistry. However, the laws of physics are completely insufficient to determine which shapes or organizations will evolve in the living world. Once a particular biological organization has emerged, it will strongly constrain the behavior of its components.
For example, the coding of amino acids by specific triplets of bases in the DNA is not determined by any physical law. A given triplet might as well be translated into a multitude of other amino acids than the one chosen in the organisms we know. But evolution happens to have selected one specific "attractor" regime where the coding relation is unambiguously fixed, and transgressions of that coding will be treated as translation errors and therefore eliminated by the cell's repair mechanisms.
A final example from the cultural sphere. Although our basic measuring units (e.g. second or meter) are defined by physical means (e.g. through the invariant length of a particular wave lenght of a particular type of electromagnetic radiation), the specific choice of unit is wholly arbitrary. The laws of physics impose the constraint that the wave lenght of light emitted by a particular quantum transition as measured in the units we choose must always be the same. However, the choice of a particular unit is not determined by those laws of physics. It is the result of a complex socio-cultural evolution in which different units are proposed for the most diverse reasons, after which one unit is eventually selected, perhaps because it has been used a little bit more frequently by slightly more authoritative sources than the other ones. Once the standard gets established, it becomes a constraint which everybody is supposed to follow. The whole (the socio-cultural system with its standards) determines the behavior of the parts (the measurements made by individuals).
References:
| Synopsys: |
This proposition is to be understood in both directions: "equal effects have (are the results of) equal causes" applies as well.
The former expression denotes predictability: if we know the effect e1 of c1, and we know that another cause c2 is equal to c1, then we can predict that c2 will have an effect e2 equal to e1. The latter (converse) expression denotes reversibility: if we know two equal effects e2 and e1, and we know that e1 was caused by c1, then we can retrodict the cause c2 equal to c1 of e2, that is to say we can reverse the process (at least informationally). The whole expression can also be reformulated as :
| distinct causes have distinct effects (and vice-versa). (2) |
This expression can be summarized as distinction conservation: if two situations were initially distinct they will remain distinct in all further evolutions, and have been distinct during all previous evolutions.
An equivalent principle defining causality is that of covariation:
| when a cause is varied (replaced by a cause different in some respect), its associated effect will vary (3) |
The problem with these different definitions is that if they are considered at the most fundamental, microscopic level, they become trivial, unable to produce any practical predictions. In (1), if "equal" is taken to mean "identic" we get the tautologous result that if a cause is identic to itself (which it always is), then its effect must be identic to itself (which can be seen as a paraphrase of the principle of the identity of the indistinguishables). In (2) or (3) we get that if an initial state is replaced by a state that is not identically the same, then the resulting state will not be identically the same. If the state is a "state of the world", encompassing all that exists, then it is obvious that after a change of that state the resulting state will not be identically the same as the one resulting before the change. (Otherwise we would not be able to retrodictively distinguish the two initial states, since no difference whatsoever would be left).
We may call such a radical interpretation of (1) and (2) the "microscopic causality" principle. This principle does not allow us to make any predictions. In practice, "equal" is therefore interpreted as "similar": two causes or events may be different in some way, yet behave the same as far as the things we are interested in are concerned.
However, recent advances in non-linear dynamics have shown that in general dynamic systems are chaotic, in the sense that small differences in initial conditions can lead to enormous differences in later conditions, so that any "similarity" between two initial states is lost. In such cases the causality principle becomes practically meaningless.
For example, consider a coin vertically resting on its side in an unstable equilibrium. When it falls, we will not look for the cause of it falling down this side rather than that side, but rather consider it a chance event. The reason is that the coin in an unstable equilibrium is so sensitive that it will covary with the tiniest variation in its neighbourhood: a little bit of wind, a vibration of the table, an irregularity in the surface, or even a random distribution of air molecules so that a little bit more molecules bump against one side rather than against the other. The coin follows the microscopic causality principle: the slightest difference in initial conditions makes a difference in results.
In practice, the causality principles mentioned above only make sense when equality or distinction can be interpreted macroscopically, by means of boundaries between equivalence classes of causes and effects, so that microscopic differences between causes within one equivalence class can be ignored and only the macroscopic differences between the classes need to be taken into account. This is "macroscopic causality". However, macroscopic causality will only work in certain cases (e.g. when the dynamics is non-chaotic), and therefore cannot be seen as a universal principle.
The classical world view can be characterized by the assumption that macroscopic causality, or more generally distinction conservation, is always valid. The non-classical view, which appears in quantum mechanics and far-from-equilibrium thermodynamics, is then characterized by distinction non-conservation. That means that initially distinct states may lead to the same result (distinction destruction), or that the same state might lead to distinct outcomes (distinction creation). This requires more general principles of evolution and self-organization, based on variation and selection. The fact that macroscopic causality itself works in certain cases may be explained by these principles.
Reference: Heylighen F. (1989): "Causality as Distinction Conservation: a theory of predictability, reversibility and time order", Cybernetics and Systems 20, p. 361-384.
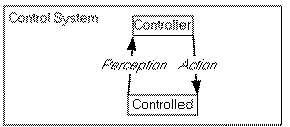
Control is the operation mode of a control system which includes two subsystems: controlling (a controller) C, and controlled, S. They interact, but there is a difference between the action of C on S, and the action of S on C. The controller C may change the state of the controlled system S in any way, including the destruction of S. The action of S on C is formation of a perception of system S in the controller C. This understanding of control is presented in Fig.1.
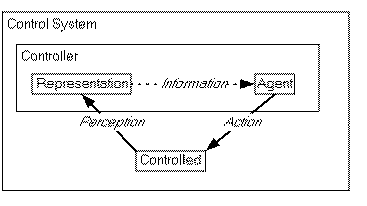
In Fig.2 we define the concept of perception. We see in the controller an agent which is responsible for its actions, and a representation of the controlled system, which is an object whose states we identify with perceptions. The relation between representation and agent is described as a flow of information: the actions of the agent depend on this flow. Thus the action of S on C is limited, in its effect, by changing only S's representation in C, not the rest of the system. Thus the asymmetry of the control relation: C controls S, but S does not control C. The action of S on C is "filtered" through the representation: its effect on C cannot be greater than allowed by the changing state of the representation.
Of course, two systems can be in a state of mutual control, but this will be a different, more complex, relation, which we will still describe as a combination of two asymmetric control relations.
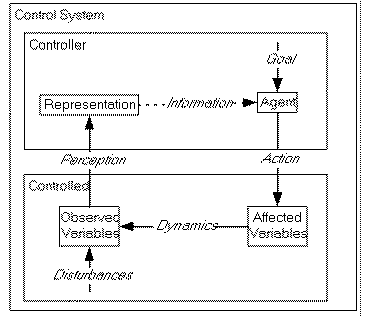
In many cases the controlled system can be also seen in greater detail, which is done in Fig.3. We describe the controlled system using some variables and distinguish between the variables directly affected by the controller, from the variables which are observed by the controller in perception. The causal dependence of the observed variables on the affected variables is determined by the intrinsic dynamics of the system. We also must not forget about the effect of uncontrollable disturbances on the observed variables.
In Fig.3 we also made an addition to the controller: it now includes one more object which influences the agent: goal. The agent compares the current representation with the goal and takes actions which tend to minimize the difference between them. This is known as purposeful behavior. It does not necessarily result from the existence of an objectified goal; the goal may be built into the system -- dissolved in it, so to say. But a typical control system would include a goal as a an identifiable subsystem.
Even though the relation of control is asymmetric, it includes a closed loop. Looked from the controller, the loop starts with its action and is followed by a perception, which is an action in the opposite direction: from the controlled to the controller. This aspect of control relation is known as feedback.
The concept of control is the cornerstone of cybernetics. The basic control scheme which we have defined in this node is the unit from which complicated cybernetic systems are created by nature and man. For this reason, our definition is pretty wide: we want our building unit to be as universal as possible. In particular, we see as special cases of control some systems which most present authors would, probably, not call control.
The different components (e.g. perception, action, ...) of the control loop we have enumerated can in the limit be absent. This leads to different "degenerate" or "limit" cases, which we would not usually see as control systems, but which still share many properties with the more elaborate control scheme. Specific instances of this control scheme can further differ in the presence or absence of different attributes or properties characterizing control systems: separability, contingency, evolvability, asymmetry, ... This leads to a very broad view of control in which many very important types of system can be classified, as shown by many examples of control systems. The abstract scheme can also be mapped on different other schemes for control by authors such as Ashby, Powers and Meystel, and on an older definition in terms of statements and commands.
A less tragic example is a programmable electric oven which executes its program without any feed-back from the cooked food.
A hydrogen molecule can be treated as a harmonic oscillator. Here the controlled system S consists of two protons at a distance x from each other. The agent which is embedded in S is the relative momentum of the protons in the center-of-mass coordinate system; it causes protons to move with respect to each other.
The controller C is the electron shell which holds the protons together at a certain equilibrium distance x0 by exerting on them a force which acts against the coulomb repulsion. (This force is quantum-mechanical in its origins, but this does not prevent us from considering oscillations classically). The distance x is a representation of the two-proton controlled system for the controller, the shell, but there is no part of the controller that would keep x: it is a feature of the proton pair, i.e. the controlled system. Also, there is no separate subsystem to keep the goal of the controller, but it functions as if the goal was to keep the distance x close to x0.
We shall now see that the control processes in a classical oscillator result from the interplay of the three fundamental factors in classical mechanics: coordinate, momentum, and force. The three arrows in our control scheme: action, perception and information will be described by the three familiar equations of the classical oscillator.
Nothing happens as long as the protons are at the equilibrium distance x0 and at rest with respect to each other. Suppose some uncontrollable disturbance pushes one of the protons passing to the controlled system some momentum p. The coordinate x starts changing according to the equation:
dx/dt = p/m (perception)
In terms of the control scheme this is perception, because the agent p of the controlled system determines the representation.
The change in the representation informs the agent F of the controller, the shell, which is assumed to be proportional to the change of x and opposite in direction:
F = -k(x-x0) (information)
This force acts on the proton pair, causing the change of the momentum according to the equation:
dp/dt = F (action)
This will start stopping the movement of the protons and finally will reverse it. In this manner, unstopping oscillations will follow, which will keep the distance x close to x0 (assuming that the initial push was in certain limits).
Properties of a Control System, Spatial separability of controller from controlled, Temporal separability of controller from controlled, Contingency of perception-action relation, Evolvability of the Controller, Filtering of the Controlled, Amplification of the Control Signal,
Control Theory, has proposed the following general scheme to represent negative feedback control mechanisms. This scheme is very similar to our scheme for control except that it tries to be quantitative, whereas ours is qualitative. By the fact that it is quantitative, there are no sharp distinctions between different cases of control, but only larger or smaller values of the relevant variables. This is in particular interesting for the asymmetry of control, which is automatically assumed in our scheme, while in Powers' scheme it derives from the fact that one variable is much larger than another one.
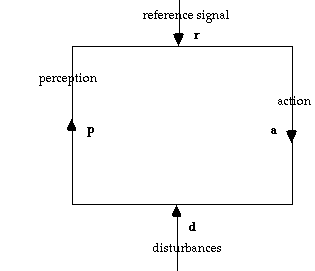
The scheme consist of a feedback loop with two inputs, the reference signal r (equivalent to our "goal") and the disturbance d. The arm of the loop going from r to d is called the action, a. The one going from d to r is called the perception, p. The relation between these elements should be such that the perception is brought as closely as possible to the reference, by the action compensating for the effect of the disturbance. In the simplest case, each component can be represented as a one dimensional variable, and the relation between them by two linear expressions:
| a = K (r - p) | (1) |
| p = E (d - a) | (2) |
The action is a function of the difference between the reference level and the perceived level. The larger the deviation between perception and goal ("error"), the larger the correcting action needed. Similarly, the perceived state is a function of the difference between the disturbance and the compensating action. K and E are two constants expressing characteristics of the control system. To better understand their meaning, the system of equations can be solved for a and p. This produces the following expressions:
| a = KE(r/E - d)/(KE + 1) | (3) |
| p = KE(r - d/K)/(KE - 1) | (4) |
Until now, the whole scheme is symmetric with respect to permutations of (r, a) with (d, p). In Fig 1, we can turn the loop upside down, and then the reference becomes the disturbance and the action becomes the perception. However, this does not accord with our intuitive understanding of control as an asymmetric relation, in which the controller (r and a) controls the perturbations (d and p), but not the other way around. The asymmetry can be introduced by assuming that K is very large, and much larger than E. In that case, through equation (4), p becomes almost equal to r:
K >> E => p ~= r
This means that control is achieved: the deviation between goal and perception is practically reduced to zero. Whatever the size of the disturbance d, the control system manages to keep the state very close to its preferred state r. K expresses the factor of "amplification": the smallest deviation (r - p) is immediately sensed and compensated by a large action a = K (r - p). Although the action is large relative to the deviation, as expressed by eq. (3), it does not need to be large in absolute terms. The reason is that because of the negative feedback relation the deviation is immediately compensated before it can grow larger. Thus, really large actions will never be needed, since deviations always remain small. The amplification factor measures both the "power" of the control system, in the sense of the amount of energy it has available to take action, and its "sensitivity", in the sense of the precision with which is responds to the tiniest deviations. Since the scheme is symmetric in E and K, we can make a similar interpretation of the implications of a large factor E. This would mean that the perception is very sensitive to disturbances, in other words that the tiniest perturbation would make the system deviate from the reference level. This describes a situation with poor or no control. In conclusion, the larger K with respect to E, the less the perception will deviate from the goal, and the better the control.
See also:
introduction to perceptual control theory
Java Demonstrations of Perceptual Control
PRNCYB-L discussion on: Definition of Control according to Powers and BoydExample: you drive a car. Here C is you, and S is your environment: the car, the road, etc. You receive visual and audio messages from the environment and vary the position of the car's wheels to keep it on the road. This is a direct change of the state of the controlled system. But you can consider your steering wheel as an information channel, through which you send commands to the wheels proper.
Another example: remote control of a missile. Here you receive information from the missile's sensors and send commands to it. But if you do not wish, for some reason (although this is not really reasonable) to separate the information channel from the missile and consider them together as the controlled system S, then you exercize a direct intervention.
The relation between a language and metalanguage, or theory and metatheory, is also a control relation. Here S is the system that uses the language, and C is the system that uses metalanguage. We create metalanguage and metatheory in order to examine the works of the language and the theory. The flow of descriptive information is from the language S to the metalanguage C. The result of our examination of the language and theory is classification and construction of more sentences of the language and more theories - this is alteration of the state of the language S.
de Rosnay
In every feedback loop, as the name suggests, information about the result of a transformation or an action is sent back to the input of the system in the form of input data. If these new data facilitate and accelerate the transformation in the same direction as the preceding results, they are positive feedback - their effects are cumulative. If the new data produce a result in the opposite direction to previous results, they are negative feedback - their effects stabilize the system. In the first case there is exponential growth or decline; in the second there is maintenance of the equilibrium.
Positive feedback leads to divergent behavior: indefinite expansion or explosion (a running away toward infinity) or total blocking of activities (a running away toward zero). Each plus involves another plus; there is a snowball effect. The examples are numerous: chain reaction, population explosion, industrial expansion, capital invested at compound interest, inflation, proliferation of cancer cells. However, when minus leads to another minus, events come to a standstill. Typical examples are bankruptcy and economic depression.
In either case a positive feedback loop left to itself can lead only to the destruction of the system, through explosion or through the blocking of all its functions. The wild behavior of positive loops - a veritable death wish - must be controlled by negative loops. This control is essential for a system to maintain itself in the course of time.
Negative feedback leads to adaptive, or goal-seeking behavior: sustaining the same level, temperature, concentration, speed, direction. In some
cases the goal is self-determined and is preserved in the face of evolution:
the system has produced its own purpose (to maintain, for example,
the composition of the air or the oceans in the ecosystem or the concentration of glucose in the blood). In other cases man has determined the
goals of the machines (automats and servomechanisms).
In a negative loop every variation toward a plus triggers a correction
toward the minus, and vice versa. There is tight control; the system
oscillates around an ideal equilibrium that it never attains. A thermostat
or a water tank equipped with a float are simple examples of regulation
by negative feedback.
(see the paper "Semantic
Control Systems").
"Semantic
Control Systems").
See also:
Semiotics on the web
Intelligent Systems: A Semiotic Perspective
General Information on Biosemiotics, with lots of interesting links
Algebraic Semiotics
Perhaps the most famous (and some would say the only successful) principle of cybernetics recognized by the whole Cybernetics and Systems Science community is Ashby's Law of Requisite Variety (LRV) \cite{ASR56}. The Law has many forms, but it is very simple and common sensical: a model system or controller can only model or control something to the extent that it has sufficient internal variety to represent it. For example, in order to make a choice between two alternatives, the controller must be able to represent at least two possibilities, and thus one distinction. From an alternative perspective, the quantity of variety that the model system or controller possesses provides an upper bound for the quantity of variety that can be controlled or modeled.
Requisite Variety has had a number of uses over the years \cite{DEJ87,POB76}, and there are a number of alternative formulations. As mentioned in section variety, variety can be quantified according to different distributions, for example probabilistic entropies and possibilistic nonspecificities. Under a stochastic formulation, there is a particularly interesting isomorphism between the LRV, the 2nd Law of Thermodynamics \cite{ZWM78c,STS87}, and Shannon's 10th Theorem \cite{SHCWEW64}.
Heylighen:
The larger the variety of actions available to a control system, the larger the variety of perturbations it is able to compensate.
This is another application of the principle of selective variety, formulated above. However, a stronger form of Ashby's Law (1958), "the variety in the control system must be equal to or larger than the variety of the perturbations in order to maintain stability", does not hold in general. Indeed the underlying "only variety can destroy variety" assumption is in contradiction with the principle of asymmetric transitions which implies that spontaneous decrease of variety is possible. For example, the bacterium described above disposes of a minimal variety of only two actions: increase or decrease the rate of random movements. Yet, it is capable to cope with a quite complex environment, with many different types of perturbations (Powers, 1989). Its blind "transitions" are normally sufficient to find a favourable ("stable") situation, thus escaping all dangers.
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
As is well known \cite{CORASR70}, in order for there to be a proper coordination of actions to perception the system must be able to select the correct choice. The ability of the system to avoid incorrect or unviable choices is a constraint on the behavior of the control system. If no such constraint existed, the system would have to try out actions blindly, and the larger the variety of perturbations, the smaller the probability that those actions would turn out to be adequate.
Thus all viable modeling and aniticipatory control requires an intermediate quantity of variety: enough to satisfy the LRV that it is possible to represent all necessary control systems; but not too much to violate the Law of Requisite Constraint and leave the system with insufficient "knowledge" about its environment.
This intermediary balance between freedom and constraint in viable systems has long been noted in information theory \cite{ZWM84a}. This can be measured in the intermediate entropy values that can be measured in symbol systems such as linguistic texts and chromosomes.
| Synopsys: |
This principle reminds us that a variety of actions is not sufficient for effective control, the system must be able to (vicariously) select an appropriate one. Without knowledge, the system would have to try out an action blindly, and the larger the variety of perturbations, the smaller the probability that this action would turn out to be adequate. Notice the tension between this law and the law of selective variety: the more variety, the more difficult the selection to be made, and the more complex the requisite knowledge.
"Knowing" signifies that the internal (vicarious) selector must be a model or representation of the external, potentially selecting perturbations. Ideally, to every class of perturbations there corresponds a class of adequate counteractions. This correspondence might be represented as a homomorphism from the set of perturbations to the set of (equivalence classes of) compensations. However, this does not imply that knowledge would consist of a homomorphic image of the objects in the environment. Only the (perturbing) processes of the environment need to be represented, not its static structure.
An equivalent principle was formulated by Conant and Ashby (1970) as "Every good regulator of a system must be a model of that system". Therefore the present principle can also be called the law of regulatory models.
Reference: Heylighen F. (1992): "Principles
of Systems and Cybernetics: an evolutionary perspective", in:
Cybernetics and Systems '92, R. Trappl (ed.), (World Science, Singapore),
p. 3-10.
| Synopsys: |
[Node to be completed]
The statement of the Law of Requisite Hierarchy by Arvid Aulin, is followed by:
". . . . [In other words], the lack of regulatory ability can be compensated to a certain extent by greater hierarchy in organization."(Cybernetic Laws of Social Progress, p. 115)
Eigenvalues
Fixed points
Invariant relations
Symmetries
Consider a system S of any kind. Suppose that there is a way to make some number of copies from it, possibly with variations. Suppose that these systems are united into a new system S' which has the systems of the S type as its subsystems, and includes also an additional mechanism which controls the behavior and production of the S-subsystems. Then we call S' a metasystem with respect to S, and the creation of S' a metasystem transition. As a result of consecutive metasystem transitions a multilevel structure of control arises, which allows complicated forms of behavior.
In Turchin's book "The Phenomenon of Science" (Columbia University Press, 1977) it is shown that the major steps in evolution, both biological, and cultural, are nothing else but metasystem transitions of a large scale. The concept of metasystem transition allows us to introduce a kind of objective quantitative measure of evolution and distinguish between evolution in the positive direction, progress, and what we consider an evolution in the negative direction, regress (cf. the direction of evolution). In the present node we outline the main ideas of this book.
When we speak of cybernetic systems, we can describe them either in terms of their structures, or phenomenologically, in terms of their functioning. We cannot claim at the present time that we know the structure of the human brain well enough to explain thinking as the functioning of that structure. However we can observe evolutionizing systems and make conclusions about their internal structure from a phenomenological description of how they function.
From the functional point of view the metasystem transition is the case where some activity A, which is characteristic of the top control system of a system S, becomes itself controlled as a metasystem transition from S to S' takes place. Thus the functional aspect of metasystem transitions can be represented by formulas of this kind:
control of A = A'
When a phenomenological description of activities of some systems fits this formula we have all reasons to believe that this is a result of a metasystem transition in the physical structure of the systems. Here is the sequence of metasystem transitions which led, starting from the appearance of organs of motion, to the appearance of human thought and human society:
A metasystem transition is fundamentally a process of systems formation. A metasystem transition results in the creation of a new system, and thus new entities which are stable at a higher level of analysis.
Following the metasystem transition the entities (now subsystems) are under the control of the new system. The behavior of the whole is constrained by the parts (a "reductionistic" view), but the behavior of the parts is at the same time constrained by the whole (a "holistic" view). The control of the metasystem decreases the freedom of the subsystems: they are constrained, perhaps not entirely, by the metasystem into certain pathways of activity (see cite{CAD90}).
The new systemic level has its own attributes, and its own variability. Thus the total freedom of the overall metasystem now becomes split into two: that of the parts and that of the whole. How that freedom is distributed is a crucial question, and has some extremes. While the freedom of the subsystems is decreased, the overall freedom and adaptivity of the overall system may increases.
We can identify one limit as an isolated system, in particular an isolated thermodynamic system. As is well known cite{ROW82}, under these conditions the thermodynamic system goes to equilibrium, and the macroscopic properties of the metasystem (pressure, temperature) become completely stable, and show no variation. Simultaneously, according to the second law, the statistical entropy, and thus the variation, of the subsystems (the molecular components) is maximized. Thus under these conditions the entire freedom of the system is "pushed down" to the components: maximal stability of the whole is traded for maximal instability of the parts.
The converse case where the parts become completely constrained occurs in the case of a machine. The structure of a machine constrains its parts along deterministic pathways cite{ASR56}.
The "law of the branching growth of the penultimate level" might be seen as the beginning of a more detailed dynamics of MST's. It states that after the formation, through variation and selection, of a control system C, controlling a number of subsystems Si, the Si will tend to multiply and differentiate. The reason is that only after the formation of a mechanism controlling the Si it becomes useful to increase the variety of the Si. Complementarily, the larger the variety of Si to be controlled, the more important it is to develop and refine the control mechanism C. The development of C and the multiplication of the Si are thus mutually reinforcing processes. The result is that an MST is characterized by a positive feedback where a small evolutionary change is strongly accelerated, after which it slows down again by the time a new level of equilibrium is reached.
Initially, the integration of replicated subsystems Si can take place only on a small scale. This is the law of combinatorics. The trial and error method can work only on combinations of relatively few elements; otherwise the number of possible combination becomes so huge that there is no chance to find the needle of a stable configuration in this bundle of hay.
However, when the needed combination is found, and a new controlling agent C has emerged, it becomes, typically, possible to control almost any number of integrated subsystems, and this is advantageous for stability because of the geometric and combinatorial factors mentioned above. There starts an integration on a grand scale. The emergent agent is on the ultimate control level of the emergent system; the integrated subsystem make up the penultimate level. A metasystem transition leads to multiplication of these subsystems. When nature discovered the principle of coding protein forms with sequences of four nucleotides, the growth of the number of nucleotides began, resulting in huge molecules with many thousands of nucleotides. When the concept of a cell that can cooperate with other cells emerged, multicellular organisms started being formed with growing numbers of integrated cells, until they reached the sizes of present day animals. The same with human society. A well organized society starts growing exponentially.
Although the growth of complexity during evolution is not universal (many systems evolve towards higher simplicity), it appears as the most striking factor from a long-term perspective. Most of the time this complexity increase, and evolution in general, occurs rather slowly or continuously, but during certain periods evolution accelerates spectacularly. This results in changes which from a long term perspective may be viewed as momentous events, separating discrete types of organization. Each time a higher level of control or organization has developed we say that a Metasystem Transition (MST) has taken place.
The MST concept makes it possible to reconstruct the sequence of evolutionary events from the beginnning of time to the present as a partially ordered series of metasystem transitions. These transitions can be roughly classified in four categories or "tracks":
For a chronology of some of these transitions, see the Cosmological and Evolutionary/Geological Timelines.
The history of biological evolution is marked by a number of metasystem transitions, including: the origin of life itself, the development of the modern cell from the aggregation of pre-cellular organelles (the transition from prokaryotes to eukaryotes); the coordination of single cell organisms into multi-cellular organisms; and the origin of sexual reproduction.
A detailed treatment of these different developments can be found in:
Maynard Smith J. & Szathmàry E. (1995): Major Transitions in Evolution, (W.H. Freeman, Oxford).
From the book cover:
(...). This is the first book on all these major transitions. In discussing such a wide range of topics in one volume, the authors are able to highlight the similarities between different transitions- for example, between the union of replicating molecules to form chromosones and of cells to form multicellular organisms. The authors also show how an understanding of one transition sheds light on others.A common theme in the book is that entities that could replicate independently before the transition can replicate afterwards only as as part of a larger whole. Why, then, does selection between entities at the lower level not disrupt selection at a higher level? In answering this question, the authors offer an explanation for the evolution of cooperation at all levels of complexity.
It is rather apparent that the level of the living organism, and in particular the biochemistry of macromolecules like DNA, is the first in evolutionary history to manifest the properties of the semantic coding relationships necessary for anticipatory control. Thus the problem of the origin of the first organism is essentially that of the first metasystem transition leading to an anticipatory control system.
See also: Christian de Duve "The Beginnings of Life on Earth"
For a control-theoretic scenario for the origin of life, see Powers's paper "The Origins of Purpose"
"The path from a unicellular condition to a multicellular one has been well-traveled. Of the same 23 monophyletic protist groups, fully 17 have multicellular representatives. The path from multicellularity to cellular differentiation, however, proved a far less porous filter. Of the 17 multicellular taxa, only 3 groups-the plants, the fungi, and the animals-have developed cellular differentiation in more than a handful of species. With the evolution of cellular differentiation, kingdoms were made of some protist groups; yet we know virtually nothing as to why this transition was closed to all but a few taxa." (Buss, 1987, p. 70In agreement with Turchin's definition of Metasystem Transition, Buss portrays the first stage of multicellularity without differentiation of function, except for accidents of location in the adhering mass. With differentiation comes the distinction between germ cells and somatic cells. Somehow the germ cells exchange proliferation by fission within the organism for reproduction by seed across generations, and the specialized somatic cells gain in reproductive opportunities by fission within the organism. It helps in achieving differentiated multicellularity that all of the cells are identical twins in terms of chromosomal genes (implying a shared control). This has not removed the competition among cells for reproduction by fission. Adaptive distribution of such specialized cell proliferation requires additional controls. These are not under any centralized coordination, but are achieved through a widely distributed variety of inducing and inhibiting adjacencies. Keeping these controls tuned so that the integrated division of labor which produces a multicellular-organismic functionality is preserved requires a node of selection at the whole organism level. Such a node was also a prerequisite for its development. This node is implemented by differential propagation of the seeds produced by the germ cells.
Reference:
Selection
of Organization at the Social Level: obstacles and facilitators of metasystem
transitions ", World Futures: the Journal of General Evolution
45, p. 181-212.
Variation of DNA can be found in different mechanisms of genetic change: mutations, recombinations, copying errors, ... In order to find a metasystem transition, we need a mechanism that controls or constrains such changes in a non-random way. Although geneticists are still learning a lot about the underlying molecular processes, there is one mechanism which is clearly not the effect of random noise, sexuality. It can be defined as the constrained variation of DNA sequences by recombination with a second sequence from another organism of the same type.
Sexuality makes it possible to increase genetic variety without the dangers of random mutation: since both sequences have proven their viability, is it not very likely that their recombination would be unviable. Mutations, on the other hand, are most likely deleterious. Higher variety (or "diversity" in biological terminology) of offspring implies a lower probability that all of them would be eliminated by natural selection, and a high probability that at least one of them would be more fit thna the parents. The effectiveness of recombination mechanisms for exploring large fitness spaces has been demonstrated in computer applications by genetic algorithms.
The metasystem that emerges from this metasystem transition is the species, which is defined as the set of all organisms that are capable to recombine their genes in the way mentioned. In sexual organisms, no individual organism really reproduces, since the offspring is always genetically different from the parent. The only system that can really be said to maintain and reproduce is the species as a whole, characterized by a more or less stable "gene pool", i.e. the collection of genes available for recombination.
Reference: Heylighen F. (1995): "(Meta)systems
as Constraints on Variation: a classification and natural history of metasystem
transitions", World Futures: the Journal of General Evolution
45, p. 59-85.
The origin of the nerve cell marks another major step in biological evolution. As a communicative device, the function of a nerve cell is to vary so that it can communicate information. Nerve cells can affect a variety of semantic coding relationships, allowing multicellular organisms to rapidly develop many levels of hierarchical anticipatory control. In particular, we recognize in the following schema the major steps of neural evolution:
Culture is control of thought; which is control of associating; which is control of complex reflexes; which is control of simple reflexes; which is control of movement; which is control of position.
| Synopsys: |
We still know so little about the process of thinking and the structure of the thinking brain that any theory claiming to explain this phenomenon as a whole is hypothetical. Thus, our conception of thinking must also be treated as a hypothesis. However, this conception indicates the place of thinking in the series of natural phenomena and, as we shall see, puts a vast multitude of facts together in a system. The complete absence of particular, arbitrary assumptions, which ordinarily must be made when a theory includes a structural description of a little-studied object, is another positive feature. The core of our conception is not some hypothesis regarding the concrete structure and working mechanism of the brain, but rather a selection of those functional concepts through which a consistent and sufficiently convincing explanation of the facts we know about thinking becomes possible.
Thus, we assert that the appearance of thinking beings, which marks the beginning of a new stage--perhaps a new era--in evolution (the era of reason) is nothing short of the next metasystem transition, which occurs according to the formula
To prove this assertion we shall analyze the consequences that follow from control of associating and equate them with the forms of behavior we observe in thinking beings.
First of all, what is control of associating? Representations X and Y are associated in an animal only when they appear together in its experience. If they do not appear together (as a rule, on many occasions), the association will not arise. The animal is not free to control its associations; it has only those which the environment imposes on it. To control associating a mechanism must be present in the brain which makes it possible to associate any two or several representations that have no tendency at all to be encountered together in experience--in other words, an arbitrary association not imposed by the environment.
This action would appear to be completely meaningless. An elder tree in the garden and an uncle in Kiev--why connect these two totally unrelated facts? Nonetheless, arbitrary associating has profound meaning. It really would be meaningless if brain activity amounted to nothing more than passively receiving impressions, sorting them, grouping them, and so on. But the brain also has another function--its basic one: to control the organism, carrying out active behavior which changes the environment and creates new experience. You can bet that the alarm clock and the holder for the teapot are in no way associated in your consciousness. Nor in the consciousness of your three-year-old son. However, this is only for a certain time. One fine day, for some reason an association between these two objects occurs in the head of the young citizen and he is overcome by an insurmountable desire to rap the alarm clock with the holder. As a result, the objects enter a state of real, physical interaction.
In the metasystem transition, some thing that was once fixed and uniquely determined by external conditions becomes variable and subject to the action of the trial and error method. Control of associating, like every metasystem transition, is a revolutionary step of the highest order directed against slavish obedience by the organism to environmental dictatorship. As is always true in the trial and error method , only a small proportion of the arbitrary associations prove useful and are reinforced, but these are associations which could not have arisen directly under the influence of the environment. And they are what permits a reasoning being those forms of behavior which are inaccessible to the animal that was frozen in the preceding stage.
Reference:
Turchin V. (1977): The Phenomenon of Science. A cybernetic approach to human evolution, (Columbia University Press, New York).
We have loosely used the informal concept of the "organism" as a distinct kind of living entity. We must recognize that this distinction is largely arbitrary, and only useful in limited domains. A number of examples, such as viruses, beehives, slime molds, and other symbiotic and parasitic relationships threaten to blur the distinction between the living organism and the community as the elemental living system.
Yet if we assume the existence of distinct organisms, then the hierarchy of neural evolution is marked by a series of metasystem transitions within organisms. But at the same time, metasystem transitions also occur which bring organisms together in groups. Some simple examples include breeding populations and the dynamics of fish schools and bird flocks. When these group controls are very strong, some of the more marked transitions (e.g. the development of multicellular organisms) result.
But when the group controls are considerably weaker, we have the existence of societies of organisms. The most integrated form of such societies can be found in the social insects: ants, bees and termites. Human society is much less strongly integrated but much more complex. Higher-level societies are usually marked by culture, which can be defined simply as models which are inherited between organisms in a non-genetic manner. We can define such non-genetic information, when carried between people, as memes. Memes, similar to genes, undergo a variation and selection type of evolution, characterized by mutations and recombinations of ideas, and by their spreading and selective reproduction or retention.
As outlined in our discussion of cognitive evolution, thought can be understood as the ability to control the production, reproduction and association of memes in the minds of humans. What follows is the possibility of evolution at the memetic level. The emergence of human thought marks the appearance of a new mechanism of evolution: conscious human effort instead of natural selection. The variation and selection necessary for the increase of complexity of the organization of matter now takes place in the human brain; it becomes inseparable from the willed act of the human being.
Thus the emergence of human intelligence and memetic evolution precipitated a further, currently ongoing, Metasystem Transition, which is the integration of people into human societies. Human societies are qualitatively different from societies of animals because of the ability of the human being to create (not just use) language. Language serves two functions: communication between individuals and modeling of reality. These two functions are, on the level of social integration, analogous to those of the nervous system on the level of integration of cells into a multicellular organism. The body of a society is the bodies of all people plus the things made by them. Its "physiology" is the culture of society.
Using the material of language, people make new --- symbolic --- models of reality (scientific theories, in particular) such as never existed as neural models given us by nature. Language is, as it were, an extension of the human brain. Moreover, it is a unitary common extension of the brains of all members of society. It is a collective model of reality that all members of society labor to improve, and one that preserves the experience of preceding generations.
Initially there was no division of labor or caste specialization. Mother and infertile daughters were all capable of all tasks of food-gathering and brood-care. While it was in the inclusive-fitness interests of each of the sterile workers to become fertile, it was also in the inclusive-fitness interests of each to keep her sisters sterile, as by distributing the queen's fertility-inhibiting pheromone to her sisters (including those in larval stages) and by eating the haploid drone eggs that some of her supposedly sterile sisters might produce. Once worker sterility was dependably achieved, then selection by colony could dominate because the individual-vs.-individual genetic competition had been almost completely eliminated. From this point on, the elaborate division of labor into the several worker and soldier castes could develop (Wilson, 1971; Campbell, 1983).
Note that in none of the social insects are the sterile workers and/or soldiers genetically identical, nor do the castes differ systematically in their genetic composition. The differentiation into worker, soldier, and queen is achieved by differential feeding and pheromone exposure in early development. Note, too, that in the social insects the genetic competition among the cooperators has not been entirely suppressed, and shows itself in many minor ways such as kin-favoritism of workers in caring for larvae, and among the bees, at least, when the queen is removed, disruptive genetic competition among the disinhibited formerly-sterile workers (Seeley, 1985, 1989; Winston and Slessor, 1992).
The anatomical differentiation among the castes is controlled by distributed (rather than centralized) inhibitions. So, too, the communication and coordination among the castes. Some dozen different pheromones are involved, all released and distributed in automatic reflex ways. Quasi-entropic effects of mutations produce discoordination. Again, it is selection by whole nest survival that keeps these dozens of adjustments tuned for whole-nest functionality. Unique nest odors prevent individuals from transferring membership from nest to nest, further ensuring whole-nest selection.
Reference: Heylighen F. & Campbell D.T. (1995): "Selection
of Organization at the Social Level: obstacles and facilitators of metasystem
transitions ", World Futures: the Journal of General Evolution
45, p. 181-212.
Our previous position accepted the following:
This simple point of view we are now ready to substantially modify for social control mechanisms within primary groups, retaining its relevance for secondary groups. One influence is the increased plausibility of biological group selection as seen by evolutionary biologists (cf. Wilson and Sober, 1994). All along, biological evolution has been credited for the human capacity for culture, including competent communication of useful information between individuals. But even in much less social animals, social communication creates a niche for self-serving deception, and biological group selection may be needed to keep the rate of such parasitism low enough so that there is a net collective communicative advantage. The resulting proximal mechanisms would include mutual monitoring and retaliation for "immoral" behavior (an analogue for the mutual enforcement of sterility among the social insect castes). We humans probably have an innate fear of ostracism, and a tendency to find painful the signs of hostility on the part of those we work or live with on a regular face-to-face basis. Innate tendencies to enforce group solidarity on others would be supported by both individual and group selection and may be identified as prerequisite for group selection.
The route to a cultural-evolutionary group selection that had been proposed contained several stages that built upon biologically evolved bases (Boyd and Richerson, 1985; Campbell, 1983, 1991). While these are presented as advantageous at the individual selection level, they are both plausible routes to biological group selection and might require group selection to avoid free rider parasitism and elimination by the negative costs of the self-sacrificial altruism they produce:
Even if biological group selection has occurred in human evolution, the persistence of genetic competition among the cooperators has produced a profoundly ambivalent social animal, in sharp contrast with the sterile castes of the social insects. For humans in social organizations, organizational optimizing is in continuous conflict with optimizing individual well-being and inclusive fitness. In parallel, primary group social solidarity competes with secondary group optimization in industrial and governmental bureaucracies.
Reference: Heylighen F. & Campbell D.T. (1995): "Selection
of Organization at the Social Level: obstacles and facilitators of metasystem
transitions ", World Futures: the Journal of General Evolution
45, p. 181-212.
| Synopsys: |
|
Cultural evolution, including the evolution of knowledge, can be modelled through the same basic principles of variation and selection that underly biological evolution. This implies a shift from genes as units of biological information to a new type of units of cultural information: memes.
A meme is a cognitive or behavioral pattern that can be transmitted from one individual to another one. Since the individual who transmitted the meme will continue to carry it, the transmission can be interpreted as a replication: a copy of the meme is made in the memory of another individual, making him or her into a carrier of the meme. This process of self-reproduction, leading to spreading over a growing group of individuals, defines the meme as a replicator, similar in that respect to the gene (Dawkins, 1976; Moritz, 1991).
Dawkins listed the following three characteristics for any successful replicator:
In these general characteristics, memes are similar to genes and to other replicators, such as computer viruses or crystals. The genetic metaphor for cultural transmission is limited, though. Genes can only be transmitted from parent to child ("vertical transmission"). Memes can be transmitted between any two individuals ("horizontal transmission" or "multiple parenting"). In that sense they are more similar to parasites or infections (cf. Cullen, 1998).
For genes to be transmitted, you need a generation. Memes only take minutes to replicate, and thus have potentially much higher fecundity (see Competition between Memes and Genes). On the other hand, the copying-fidelity of memes is in general much lower. If a story is spread by being told from person to person, the final version will be very different from the original one. It is this variability or fuzziness that perhaps distinguishes cultural patterns most strikingly from DNA structures: every individual's version of an idea or belief will be in some respect different from the others'. That makes it difficult to analyse or delimit memes. This does not imply that meme evolution cannot be accurately modeled, though. After all, genetics was a well-established science long before the precise DNA structure of genes was discovered.
Examples of memes in the animal world are most bird songs, and certain techniques for hunting or using tools that are passed from parents or the social group to the youngsters (Bonner, 1980). In human society, almost any cultural entity can be seen as a meme: religions, language, fashions, songs, techniques, scientific theories and concepts, conventions, traditions, etc. The defining characteristic of memes as informational patterns, is that they can be replicated in unlimited amounts by communication between individuals, independently of any replication at the level of the genes.
Of course, the capacity of the nervous system for learning is the result of evolutionary processes at the genetic level. Yet I will here not go into detail about why that capacity has been selected. The increased fitness resulting from a nervous system that is flexible enough to adapt its behavior to many new situations, seems obvious enough. If a useful type of behavior can be learned directly from another individual by communication or imitation, that seems like a most welcome shortcut for having to discover it by personal trial-and-error. More arguments for why the capacity for meme replication has evolved genetically can be found in most texts about the recently founded domain of memetics (Moritz, 1991).
Memetics can be defined as an approach trying to model the evolution of memes (see e.g. Boyd & Richerson, 1985; Cavalli-Sforza & Feldman, 1981; Lumsden & Wilson, 1981; Csanyi, 1991; Lynch, 1998). Memes undergo processes of variation (mutation, recombination) of their internal structure. Different variants will compete for the limited memory space available in different individuals. The most fit variants will win this competition, and spread most extensively. Different criteria for the fitness of a meme, relative to other memes, can be formulated.
Variation, replication and selection on the basis of meme fitness determine a complex dynamics. This dynamics will be influenced by the medium through which memes are communicated, and the copying-fidelity, fecundity and longevity it allows. Perhaps the most powerful medium for meme transmission is the computer network, and this implies some specific characteristics for memes on the net.
As is the case with genes, it is not necessary to know the exact coding or even the exact size or boundaries of a meme in order to discuss its fitness, and thus to make predictions about its further spreading, survival or extinction within the population of competing memes. Such predictions can be empirically tested. For example, a memetic hypothesis might state that simpler memes will spread more quickly. This can be tested by observing the spread (perhaps in a controlled environment) of two memes that are similar in all respects, except that the one is simpler. Theories can also be induced from empirical observation of meme behavior "in the wild" (see e.g. Best, 1998). Given the differences in variation and selection mechanisms, it is also possible to make predictions about the competition between memes and genes.
Models for Interacting Populations of Memes: Competition and Niche Behavior. Journal of Memetics - Evolutionary Models of Information Transmission, 1.
Selfish
Memes and the Evolution of Cooperation", Journal of Ideas , Vol.
2, #4, pp 77-84.
Units, Events, and Dynamics in Memetic Evolution", Journal of Memetics (submitted)
"Memetic Science: I - General Introduction", Journal of Ideas 1, p. 1-23
Metasystems, Memes and Cybernetic Immortality, in: Heylighen F., Joslyn C. & Turchin V. (eds.), The Quantum of Evolution. Toward a theory of metasystem transitions, (Gordon and Breach Science Publishers, New York) (special issue of "World Futures: the journal of general evolution, vol. 45, p. 155-171).
Journal of Memetics - Evolutionary Models of Information Transmission.
In order to model meme structure, we may use some concepts from cognitive science. Perhaps the most popular unit used to represent knowledge in artificial intelligence is the production rule. It has the form "if condition, then action". In symbols:
If A, then B or A -> B
A represents a condition that is distinguished, B represents an action that is executed or another condition that is activated. The action leads in general to the activation of another condition. In fact a production rule can be analysed as a combination of even more primitive elements: two distinctions (which discriminate between presence and absence of the condition and the action respectively) and a connection (the "then" part, which makes the first distinction entail the second one) (Heylighen, 1991d; see also Heylighen, 1990). For example, a meme like "God is omnipotent" can be modelled as "if a phenomenon is God (distinction of God from non-God), then that phenomenon is omnipotent".
Production rules are connected when the output condition (action) of the one matches the input condition of the other. E.g. A -> B, B -> C. This makes it possible to construct complex cognitive systems on the basis of elementary rules. Even remembered melodies might be modelled in such a way, as concatenations of production rules of the type "if C (musical note distinguished), then E (note produced and subsequently distinguished)", "if E, then A", and so on.
A similar model applies to genes. A gene corresponds to a string of DNA codons, which respond to the presence of certain activating proteins, or the absence of certain inhibiting proteins (condition) by manufacturing new proteins (action). This may in turn activate further genes, depending on the present of specific chemicals in the cell, and so on. This leads to complex networks of "if... then" productions ( Kauffmann, 1992).
Distinctions can be represented as combinations (strings) of elementary yes-no (1-0) observables. Mutation or recombination of distinctions can then be modelled by either randomly changing certain binary digits in a string, or by concatenating the first part of one string (A) with the second part of another string (B), like in the following example:
Congratulations. The following URL at your site has been selected to be
included in the PC Webopaedia:
http://cleamc11.vub.ac.be/CYBSYSTH.html
A = 1001|001 mutation: A' = 1001|000
B = 0010|011 recombination ("crossing-over") of A and B:
A~B = 1000|011
Although these models do not as yet take into account distinct carriers, this looks like a very promising road to study memes formally and computationally.
Indeed, Darwinian models of genetic evolution have certainly proven their usefulness, even though it is in practice impossible to specify the exact DNA codons that determine the gene for, say, blue eyes or altruism towards siblings. As Dawkins (1976) notes, it is not necessary to be explicit about what are the constitutive elements of a gene, postulated to explain a particular characteristic or type of behavior. It is sufficient that we can distinguish the phenotypical effects of that gene from the effects of its rival genes (alleles). If we can determine the fitness resulting from these effects, taking into account the environment and the context of different, non-rival genes present in the genome, then we can make predictions about evolution.
The same applies to memes. If, for example, we observe that one meme (say Catholicism) induces its carriers to have more children than its competitors (say Calvinism and Anglicanism), and that the children tend to take over their memes from their parents, then, all other things being equal, we can predict that after sufficient time that meme will dominate in the population. Of course, in practice it is never the case that all other things are equal, but that is the predicament of all scientific modelling: we must always simplify, and ignore potentially important influences. The question is to do that as wisely as possible, and to maximally include relevant variables without making the model too complex.
Selfish
Memes and the Evolution of Cooperation", Journal of Ideas , Vol.
2, #4, pp 77-84.
For genes to be transmitted, you typically need one generation, which for higher organism means several years. Memes can be transmitted in the space of hours. Meme spreading is also much faster than gene spreading, because gene replication is restricted by the rather small number of offspring a single parent can have, whereas the amount of individuals that can take over a meme from a single individual is almost unlimited. Moreover, it seems much easier for memes to undergo variation, since the information in the nervous system is more plastic than that in the DNA, and since individuals can come into contact with much more different sources of novel memes. On the other hand, selection processes can be more efficient because of "vicarious" selection (Campbell, 1974): the meme carrier himself does not need to be killed in order to eliminate an inadequate meme; it can suffice that he witnesses or hears about the troubles of another individual due to that same meme.
The conclusion is that memetic evolution will be several orders of magnitude faster and more efficient than genetic evolution. It should not surprise us then that during the last ten thousand years, humans have almost not changed on the genetic level, whereas their culture (i.e. the total set of memes) has undergone the most radical developments. In practice the superior "evolvability" of memes would also mean that in cases where genetic and memetic replicators are in competition, we would expect the memes to win in the long term, even though the genes would start with the advantage of a well-established, stable structure. This explains why sociobiological models of human behavior can only be partially correct, as they neglect memetic factors.
For example, priests in many religions are prohibited to marry and to have children, in striking disagreement with genetic injunctions. Yet we can easily imagine that the religious meme of celibacy would have been selected because unmarried priests can spend more time and energy on "spreading the word", and hence replicating the meme.
An even more vivid example of countergenetic behavior, closely related to the issue of altruism, is that of martyrs, suicide teams, or kamikaze pilots, who are willing to give up their life in order to promote the spread of a meme: a religion, an ideology or a nation (i.e. a group defined by a common culture or ideology). In that case, the loss of one or a few carriers is compensated by the increased chances of survival for the other carriers or for the meme itself. For example, the suicide of an individual may attract the attention of other individuals to the meme he is carrying, and thus facilitate its spreading. A well-known example is Jan Palach, the Czech student who put himself to fire in order to protest the Soviet suppression of the "Prague Spring". In this case the meme would be the Czech version of "socialism with a human face".
Reference: Heylighen F. (1992) : "Selfish
Memes and the Evolution of Cooperation", Journal of Ideas , Vol.
2, #4, pp 77-84.
This highly increased efficiency of transmission directly affects the dynamics of replication. Meme transmission over the network has a much higher copying-fidelity than communication through image, sound or word. Digitalisation allows the transfer of information without loss, unlike the analog mechanisms of photocopying, filming or tape recording. Fecundity too is greatly increased, since computers can produce thousands of copies of a message in very little time. Longevity, finally, becomes potentially larger, since information can be stored indefinitely on disks or in archives. Together, these three properties ensure that memes can replicate much more efficiently via the networks. This makes the corresponding memotypes and sociotypes potentially less fuzzy.
In addition, the network transcends geographical and cultural boundaries. This means that a new development does not need to diffuse gradually from a center outwards, as, e.g., fashions or rumours do. Such diffusion can easily be stopped by different kinds of physical or linguistic barriers. On the net, an idea can appear virtually simultaneously in different parts of the world, and spread independently of the distance or proximity between senders and receivers.
Though I have received more chain-letters by email than by post, chain-letters on the net are still a minor phenomenon. Although their spread is very much facilitated by the net, the same applies to all other types of messages. That means that there is increased competition between all these different memes for a limited resource: the attention a user pays to the information he or she receives. Because chain-letters fulfil relatively few of the criteria that distinguish successful memes from unsuccessful ones, they are unlikely to win this competition.
The success of a web document can then be measured by the number of virtual copies or links pointing to it: the documents with most pointers will be used most extensively. There are already web robots, i.e. programs which automatically scan the Web, that make "hit parades" of the documents which are linked to most often. For example, it is likely that a reproduction of the works of Van Gogh on the Web will be much more popular in number of pointers than the work of some unknown 20th century painter.
Assuming that two competing documents are equally convincing otherwise, the competition will be won or lost by the number of links that point to each of them. The more pointers to a document can be found, the more people will consult it, and the more further pointers will be made. This is the same kind of self-reinforcing process that leads to conformity, to all members of a group settling on the same meme ensemble. The difference is that now there are no separate groups: on the global network, everyone can communicate with everyone, and every document can link to every other document. The end result is likely to be the emergence of a globally shared ideology, or "world culture", transcending the old geographical, political and religious boundaries. (Note that such homogeneization of memes only results for memes that are otherwise equivalent, such as conventions, standards or codes. Beliefs differing on the other dimensions of meme selection will be much less influenced by conformist selection.)
Such a networked ideology would play a role similar to that of the genome, the network of interconnected genes that stores the blueprint, and controls the physiology, of a multicellular organism. The corresponding "organism" or sociotype for this meme network would be the whole of humanity, together with its supporting technology. Individual humans would play a role similar to the organism's cells, which in principle have access to the whole of the genome, but which in practice only use that part of it necessary to fulfil their specific function.
There is a better metaphor for the emerging global network. Rather than comparing it to an organism's genome, which is normally static and evolves only because of random copying errors, it can be likened to the organism's brain, which learns and develops in a non-random way. The network functions like a nervous system for the social superorganism, transmitting signals between its different "organs", memorizing its experiences, making them available for retrieval when needed, and generally steering and coordinating its different functions. Thus, it might be viewed as a global brain.
Reference:
Heylighen F. (1996): "Evolution of Memes on the Network", in: Ars Electronica Festival 96. Memesis: the future of evolution, G. Stocker & C. Schšpf (eds.) (Springer, Vienna/New York), p. 48-57.
"An idea is something you have;
--Morris Berman
an ideology is something that has you."
What if ideas were viruses?
Consider the T-phage virus. A T-phage cannot replicate itself; it reproduces by hijacking the DNA of a bacterium, forcing its host to make millions of copies of the phage. Similarly, an idea can parasitically infect your mind and alter your behavior, causing you to want to tell your friends about the idea, thus exposing them to the idea-virus. Any idea which does this is called a "meme" (pronounced `meem').
Unlike a virus, which is encoded in DNA molecules, a meme is nothing more than a pattern of information, one that happens to have evolved a form which induces people to repeat that pattern. Typical memes include individual slogans, ideas, catch-phrases, melodies, icons, inventions, and fashions. It may sound a bit sinister, this idea that people are hosts for mind-altering strings of symbols, but in fact this is what human culture is all about.
As a species, we have co-evolved with our memes. Imagine a group of early Homo Sapiens in the Late Pleistocene epoch. They've recently arrived with the latest high-tech hand axes and are trying to show their Homo Erectus neighbours how to make them. Those who can't get their heads around the new meme will be at a disadvantage and will be out-evolved by their smarter cousins.
Meanwhile, the memes themselves are evolving, just as in the game of "Telephone" (where a message is whispered from person to person, being slightly mis-replicated each time). Selection favors the memes which are easiest to understand, to remember, and to communicate to others. Garbled versions of a useful meme would presumably be selected out.
So, in theory at least, the ability to understand and communicate complex memes is a survival trait, and natural selection should favor those who aren't too conservative to understand new memes. Or does it? In practice, some people are going to be all too ready to commit any new meme that comes along, even if it should turn out to be deadly nonsense, like:
"Jump off a cliff and the gods will make you fly."
Such memes do evolve, generated by crazy people, or through mis-replication. Notice, though, that this meme might have a lot of appeal. The idea of magical flight is so tantalizing -- maybe, if I truly believed, I just might leap off the cliff and...
This is a vital point: people try to infect each other with those memes which they find most appealing, regardless of the memes' objective value or truth. Further, the carrier of the cliff-jumping meme might never actually take the plunge; they may spend the rest of their long lives infecting other people with the meme, inducing millions of gullible fools to leap to their deaths. Historically, this sort of thing is happening all the time.
Whether memes can be considered true "life forms" or not is a topic of some debate, but this is irrelevant: they behave in a way similar to life forms, allowing us to combine the analytical techniques of epidemiology, evolutionary science, immunology, linguistics, and semiotics, into an effective system known as "memetics." Rather than debate the inherent "truth" or lack of "truth" of an idea, memetics is largely concerned with how that idea gets itself replicated.
Memetics is vital to the understanding of cults, ideologies, and marketing campaigns of all kinds, and it can help to provide immunity from dangerous information-contagions. You should be aware, for instance, that you just been exposed to the Meta-meme, the meme about memes...
The lexicon which follows is intended to provide a language for the analysis of memes, meme-complexes, and the social movements they spawn. The name of the person who first coined and defined each word appears in parentheses, although some definitions have been paraphrased and altered.
Keith Henson, "Memetics", Whole Earth Review #57: 50-55. Douglas Hofstadter, Metamagical Themas.
Howard Rheingold, "Untranslatable Words", Whole Earth Review #57: 3-8.
For a fictional treatment of these ideas, see my short story, "Memetic Drift," in Interzone #34 (March/April 1990).
+++**
Share-Right (S), 1990, by Glenn Grant, PO Box 36 Station H, Montreal, Quebec, H3C 2K5. (You may reproduce this material, only if your recipients may also reproduce it, you do not change it, and you include this notice [see: threat]. If you publish it, send me a copy, okay?)
2. Some memeticists have used `infection' as a synonym for `belief' (i.e. only believers are infected, non-believers are not). However, this usage ignores the fact that people often transmit memes they do not "believe in." Songs, jokes, and fantasies are memes which do not rely on "belief" as an infection strategy.
[meme] that their own survival becomes inconsequential in their own minds." (Henson) (Such as: Kamikazes, Shiite terrorists, Jim Jones followers, any military personnel). hosts and membots are not necessarily memeoids. (See auto-toxic; exo-toxic.)
2. A class of similar memes. (GMG)
Every scheme includes a vaccime to protect against rival memes. For instance:
+++**
Share-Right (S), 1990, by Glenn Grant, PO Box 36 Station H, Montreal, Quebec, H3C 2K5. (You may reproduce this material, only if your recipients may also reproduce it, you do not change it, and you include this notice [see: threat]. If you publish it, send me a copy, okay?)
| Synopsys: |
A fundamental problem in founding an evolutionary ethics is to explain how cooperation and altruism can emerge during evolution (Campbell, 1979). "Weak" altruism can be defined as behavior that benefits more to another individual than to the individual carrying out the behavior. "Strong" altruism denotes behavior that benefits others, but at one's own cost (Campbell, 1983). Both are common and necessary in those highly cooperative systems, which Campbell calls "ultrasocial". Ultrasociality refers to a collective organization with full division of labor, including individuals who gather no food but are fed by others, or who are prepared to sacrifice themselves for the defense of others. In the animal world, ultrasocial systems are found only in in the social insects (ants, bees, termites), in naked mole rats, and in human society (Campbell, 1983).
Highly developed systems of cooperation and mutual support can be found in all human societies. Yet we still do not have a satisfactory explanation of how such social systems have emerged. Therefore we also cannot determine how they would or should evolve in the future. Let us summarize the difficulty.
Evolution seems to predispose individuals to selfishness. Indeed, natural selection promotes the "fittest" individuals, i.e. the ones that maximally replicate. Individuals need resources to survive and reproduce. Finite resources imply competition among individuals.
Altruism (helping another individual to increase fitness) tends to diminish the fitness of the altruist, since more resources will be used by the helped one and less will be left for the helper. Thus, without further organization, altruism tends to be eliminated by natural selection.
Yet all ethical systems emphasize the essential value of helping others. Everybody will agree that cooperation is in general advantageous for the group of cooperators as a whole, even though it may curb some individual's freedom. Cooperation can increase the fitness of the cooperators, when the cooperators together can collect more resources than the sum of resources collected by each of them individually (synergy). This is only possible in a situation that is not a zero sum game.
For example, a pack of wolves can kill large animals (moose, deer) which no individual wolf would be able to kill. Yet, for each wolf separately the best strategy seems to consist in letting the other wolves spend resources while hunting and then come to eat from their captures. But if all wolves would act like that, all advantages of cooperation would disappear.
The optimal strategy for the collective system of all wolves is to cooperate, but the optimal strategy for each individual wolf as a subsystem is not to cooperate. In general, global optimization is different from sub(system)optimization. This is the problem of suboptimization. Since evolution tries to optimize first of all at the subsystem level, we need additional mechanisms to explain global optimization at the level of the cooperating system.
Perhaps the most fashionable approach to this problem is sociobiology (Wilson, 1975). Sociobiology can be defined as an attempt to explain the social behavior of animals and humans on the basis of genetical evolution. For example, a lot of sexual behavior can be understood through mechanisms of genetic selection reinforcing certain roles or patterns. Several genetic scenarios have been proposed to explain the evolution of cooperation. However, as we will show, none of these scenarios is really satisfactory. Therefore, we propose to look at scenarios based on the evolution of culture or memes.
See Further:
Selection of Organization at the Social Level: obstacles and facilitators of Metasystem Transitions, "World Futures: the journal of general evolution", Vol. 45:1-4 (1995), p. 181.
Evolution, Selfishness and Cooperation; Selfish Memes and the Evolution of Cooperation,Journal of Ideas, Vol 2, # 4, pp 70-84.
Chess, for example, is a zero-sum game: it is impossible for both players to win (or to lose). Monopoly (if it is not played with the intention of having just one winner) on the other hand, is a non-zero-sum game: all participants can win property from the "bank". In principle, in monopoly, two players could reach an agreement and help each other in gathering a maximum amount from the bank. That is not really the intention of the game, but I hope I have made the distinction clear: in non-zero-sum games the total amount gained is variable, and so both players may win (or lose). When they can both win by cooperating in some way, we might say that their cooperation creates a synergy.
Critique: this scenario ignores the problem of suboptimization. Within the altruistic group the greatest increase in fitness will go to those individuals that are least cooperative, since they profit from the others' altruism while doing less in return. As a result, the non-altruists will gradually overtake the altruists. Cooperative systems tend to be eroded from within by "genetic competition between the cooperators" (Campbell, 1983).
Critique: this reasoning cannot explain ultrasociality in human society at large, where there is little sharing of genes between individuals.
The "prisoner's dilemma" may be overcome by a strategy of "tit-for-tat", which reciprocates to cooperation by cooperation and to defection by defection. This makes it impossible for selfish individuals, who defect, to gain long-term advantages from reciprocal cooperators, since these will only cooperate with those that cooperate themselves. Yet two "tit-for-tat" players will spontaneously start to cooperate thus reaping the benefits of continuing synergy (Axelrod, 1984).
Critique: at the first encounter, none of the players knows how the other one will respond. In order to have a chance to start a cooperative exchange the reciprocal altruist must start with a cooperative move, which can be taken advantage of by a defector. The strategy only starts to pay when there are repeated encounters with the same individual, so that the gains of continuing cooperation outweigh the losses of first-time encounters with defectors. It also implies that players should recognize different partners and remember their last moves toward a given partner in order to choose the appropriate next move. This is insufficient to explain a complex ultrasocial system, where many encounters are first-time.
Moralizing = punishing selfishness and rewarding altruism in others. It has the advantage that it stimulates altruism, diminishes the fitness of defectors, and carries less costs than being spontaneously altruistic (Campbell, 1979).
Critique: moralism can only maintain an existing cooperative arrangement, it cannot create one from scratch. Effective moralism requires a higher order ethical system which is quite complicated to evolve by genetic means.
Several promising avenues have been proposed to explain the evolution of cooperation, but each has its limitations, and they seem ineffective as a way to explain human ultrasociality solely on the basis of genetic evolution.
Reference: Heylighen F. (1992) : "Evolution,
Selfishness and Cooperation", Journal of Ideas, Vol 2, # 4, pp
70-76.
The genetic argument for altruism towards individuals carrying the same genes (kin selection) generalizes to altruism towards carriers of the same memes. Since memes can be passed between any two individuals, not just between parent and offspring, a meme can spread to a complete cultural group. The homogeneity of the group with respect to that meme then turns meme selection into a special form of "group selection", where the group is defined by all the carriers of a given meme.
The argument that group selection promotes cooperation remains valid: cooperating groups as a whole will be more fit than non-cooperating ones, and will tend to become larger, by higher reproduction rates or by "conquering" of, or imitation by, less successful groups. This is reinforced by the fact that cooperation tends to stimulate communication, and communication contributes to meme spreading and stabilization. Thus, memes that induce their carriers to cooperate will be more fit than those that don't.
On the other hand, the argument against group selection loses its validity for memes. The argument assumes that more selfish individuals profiting from the cooperation will pass their non-altruistic genes to their offspring. Memes, however, are not directly passed from parent to offspring, but from the complete group to individual members ("multiple parenting"). Majority memes will tend to dominate, eliminating competing (inconsistent) minority memes (Boyd & Richerson, 1985). This may be reinforced through some form of "moralistic aggression" (e.g. ostracism) towards non-conforming members of the group, which additionally diminishes their genetic fitness. Thus, memes for individual selfishness will find it very difficult to invade an altruistic group.
The above argument explains why once established cooperative memes will be consolidated by selection. It does not explain where cooperative memes might initially develop from. The "tit-for-tat" strategy, introduced in a genetic framework, can be easily reinterpreted as a meme, represented by the following set of condition-action pairs (*), or the decision network below:
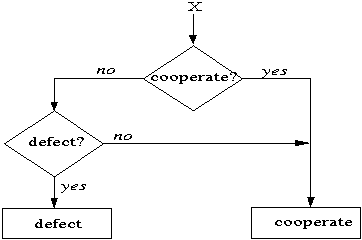
This scheme is very simple to learn: use "cooperate" as a default initial condition, and further just mimic the behavior of the partner. If the partner uses the same scheme (or an even more altruistic one) a mutually beneficial cooperative relation will develop. If the partner defects, the exchange will stop before much harm is done. Such a cognitive strategy will therefore in general be beneficial to the partners, and thus be repeated. This means that others, observing the beneficial behavioral pattern, will tend to imitate it, taking over the cognitive scheme (*). That by definition makes (*) a meme.
The difficulty with the above strategy lies in the recognition of the specific partner X. The strategy only pays off if one can distinguish partners and remember whether they cooperated or defected during the last encounter. Otherwise, every encounter is like a one-shot prisoner's dilemma, in which it pays to defect. In small groups, where interactions tend to be repeated often, a pure tit-for-tat strategy might flourish, as there would be little demands on memory. In larger groups, however, where many encounters happen for the first time, or are repeated only after a long interval in which the memory of the previous encounter might have faded, a different rule would be needed to avoid invasion by defectors.
As memes tend towards homogeneity within communicating groups (and towards heterogeneity between non-communicating groups), we might expect that after a while most members of a group G would follow the same general "tit-for-tat-like" strategy. It would then be more efficient not to distinguish between different individuals X1 or X2 in the group, but use the general rule of ingroup altruism:
if X belongs to group G, then cooperate
Whether X belongs to the group or not may be recognized by easily perceivable attributes, evolved by the group meme to facilitate distinguishing group members from members of other groups that carry different memes. "Thus the Luo of Kenya knock out two front teeth of their men, while the adjacent Kipsigis enlarge a hole pierced in their ears to a two-inch diameter" (Campbell, 1991). Since encounters with other groups will tend to be one-shot, it would pay to defect, and thus we could expect a complementary rule of outgroup hostility to evolve as a generalization of "defect from defectors":
if X does not belong to group G, then defect
Finally, the retaliation inherent in the original "tit-for-tat" strategy, as a means of protection against invading cheaters, would still be maintained in a rule of the moralistic aggression type:
if X belongs to group G and X defects, then punish X
What is considered "defection" will evolve to encompass gradually more diverse and complex patterns of behavior (e.g. lying, stealing, cheating, tresspassing rules, murdering, adultery, incest, etc.). Similary, the actions of "cooperate" and "punish" will differentiate into many different shades of behavior towards other members of the social system, dependent on the precise context. Finally, with the further spreading of related memes, what is counted as group G will tend to gradually broaden, encompassing individuals from other villages, other regions, other countries or ethnicities, until it would encompass the whole of humanity.
We have sketched a seemingly realistic scenario in which a meme complex derived from "tit-for-tat" may evolve step-by-step into an elaborate ethical and political system, capable to sustain an "ultrasocial" system as complicated as our present society. The difference between meme evolution and gene evolution (faster and more flexible adaptation, conformist and conversion selection criteria subverting genetic criteria) has allowed us to overcome the specific obstacles associated with "genetic competition among the cooperators".
Reference: Heylighen F. (1992) : "Selfish
Memes and the Evolution of Cooperation", Journal of Ideas , Vol.
2, #4, pp 77-84.
We propose Metasystem Transition Theory (MSTT) as a general model of qualitative evolution. Since every model or piece of knowledge by definition functions to make predictions, it must be an essential task of this theory to make predictions about the future of evolution itself.
In the short term, our evolutionary philosophy sees a continuing progress towards increasing intelligence, life expectancy and general quality of life. In the somewhat longer term, MSTT predicts that we will undergo a new metasystem transition that will bring us to a higher evolutionary level. This level will be characterized by evolution at the level of memes rather than genes, by the cybernetic immortality of individuals, and by the emergence of social super-organism or "global brain".
In making these predictions, a fallacy to avoid is the naive extrapolation of past evolution into the present or future. The mechanisms of survival and adaptation that were developed during evolution contain a lot of wisdom --- about past situations. They are not necessarily adequate for present circumstances. This must be emphasized especially in view of the creativity of evolution: the emergence of new levels of complexity, governed by novel laws.
The breakdown of quantitative extrapolation from existing trends is illustrated most clearly by the concept of singularity: the place where the value of a mathematical function becomes infinite, so that normal mathematical operations (differentiation, integration, extrapolation) fail. An example of a singularity in the fabric of space-time is the inside of a black hole or the origin of the universe in the Big Bang. If variables describing progress (such as technological innovation, or total amount of scientific knowledge produced) are mapped on a diagram, it is remarkable how much their increase over time is accelerating. This increase seems at least exponential but perhaps even hyperbolic (implying that infinity will be reached within a finite time). Neither form of increase can be sustained in the same form, implying that some radical change of process must take place, e.g. like a technological singularity or phase transition.
The concept of metasystem transition, through the "law of the branching growth of the penultimate level", includes such a phase of self-reinforcing acceleration of development of the last level of organization accompanied by the emergence of a next level. It seems likely that this is exactly what is happening in our present society, where the level of thinking is presently exploding, possibly to be supplemented by a "metarational" level characterized by a superhuman intelligence: the global brain.
Diminishing effort means in the first place diminishing the time needed to get the desired result. Why spend days on a task that can be performed in hours? You can use the time gained to produce more of the same, to tackle different problems, or simply to relax. Technological innovation leads directly to a speeding up of existing processes. With improved technology, houses will be built, motorcars will be assembled, food will be produced, and diseases will be cured in less time than it used to take.
Velocity has continued to augment within each major category too. Ships, trains, cars and planes move much more quickly now than they did 50 years ago. Although there are practical limits on the maximum speed of each type of vehicle, the average speed of transport continues to increase, thanks to better roads and traffic infrastructure, and more efficient methods of navigation, loading and unloading. The net effect is that people and goods need a much shorter time to reach any far-away destination. In the 16th century, Magellan's ship needed two years to sail around the globe. In the 19th century, Jules Verne gave a detailed account of how to travel around the world in 80 days. In 1945, a plane could do this trip in two weeks. Present-day supersonic planes need less than a day. Satellites circle the planet in one hour.
More important than speed records is bulk transport: the amount of goods moved per unit of time. In Magellan's time, only precious, small volume goods, such as spices, china, and jewellery, were transported over large distances. The duration and risks of the travel were simply too large. Presently, we find it normal to get most of our oil, coal, ore, and other raw materials from thousands of miles away. Giant container ships, freight trains and highways have made it economical to continuously move billions of tons around the world.
Not only matter, but energy is distributed more and more speedily. Pipelines and tankers carry oil and natural gas from other continents. For shorter distances, the electrical grid system is the most efficient, delivering power to industry and households whenever it is needed. Presently, the national power grids of neighbouring countries are starting to cross-connect, creating an international network. Thus, a factory in Denmark can receive instantaneous energy from a power station in France, or from wherever there is a high capacity available.
Better communication media diminish not only the delay between a discovery and its use by other scientists, but the delay between an invention and its acceptance in the marketplace. Studies have shown that the gap between the development of a new product and its diffusion throughout society has been steadily decreasing. The first patent for a typewriter was issued in 1714, but it was not until the end of the 19th century that typewriters were commonly used. For inventions introduced in the beginning of this century, such as vacuum cleaners and refrigerators, it would typically take some thirty to forty years before they would reach peak production. Recently, new technologies such as CD players or video recorders have swept through society in a mere ten years.
Julian Simon's analysis of development trends). Yet, the idea of progress seems to have fallen into disrepute during the last decades. On the one hand, the postmodernist thinkers emphasize the relativity of good and evil, and therefore the relativity of progress. According to them, the modern Western way of life is not objectively superior to the way of life of more "primitive" cultures, both those living today in Third World countries or in the past before industrialization. On the other hand, the enormous publicity given to negative events and developments, such as pollution, global warming, resource exhaustion, war and terrorism has created a generally pessimistic mood, where people expect things to get worse and worse. This leads many people to believe that the "noble savage" of the pre-agricultural age had in fact a much better life than the harried computer user of the present.
We believe that the question of whether progress objectively exists can be approached scientifically. An analysis of progress should be based on a well-founded theoretical framework, such as the theory of evolution, which at least in our interpretation seems to imply a preferred direction of advance towards increasing complexity and intelligence. Moreover, the theory should be based on empirical measures, comparing the overall "well-being", "happiness" or "quality of life" of past and present generations. The problem is how to quantify an abstract and subjective concept such as "quality of life" (QOL). We believe that such a quantification is possible, by looking at more concrete and objective factors which can be shown to contribute to QOL.
The sociologist Ruut Veenhoven and his coworkers have developed an extensive "World Database of Happiness", which collects the data from hundreds of polls and questionnaires in which people were asked how satisfied they are with their life. These data for different countries were correlated with a number of other variables, such as GNP per head of the population, education level, freedom of expression, etc. Not surprisingly, life satisfaction turns out to have clear positive correlation with most of the factors which we would intuitively consider as "good":
general intelligence as measured through IQ tests seems to go up with some 3 points per decade, for the 20 or so countries for which data are available (the Flynn effect). We can only conclude that empirically all major indicators of progress (sometimes grouped together in combined indicators, such as the Human Development Index, the International Index of Social Progress or the Physical Quality of Life Index) seem to be increasing unabatedly for the world as a whole. Together with a theory explaining the mechanism of this on-going improvement this should prove that progress is an objective reality. See also:
Growth Resources
Resources for Social and Economic Development
Progress and its sustainability
The Long Boom, a Wired article with an optimistic prognosis for the next 25 years
This view is outdated in several respects. On the one hand, it ignores the material limits to growth, which make things like private airplanes and trips in space prohibitively expensive. On the other hand, it fails to appreciate the unlimited capacity for change on the mental and organizational level. Rather than just enhancing or mimicking existing functions like cleaning and telephoning, technological progress will completely redefine the underlying problems. We have already learnt that it is easier and more efficient to build intelligence into a washing machine, than to build an intelligent, humanoid robot that would operate the machine the way we do it. Similarly, we would rather use enhanced telecommunications to work from home, than to travel to the office by plane, and communicate with those who stayed home.
From the new sciences, the "New Age" prophets have adopted the emphasis on networks, synergy, self-organization and holism. To this they add ideas from various mystical traditions, including Buddhism, yoga, and shamanism, and from different "alternative" approaches, like parapsychology, tarot, crystal healing and homeopathy. (Frank Capra is one of the best known authors to develop this world view combining science and mysticism.) Their main message is that humanity is quickly moving towards a higher level of consciousness. It will transcend individual awareness and its selfish concerns, and replace it by the "transpersonal" experience of belonging to a larger whole (cf. the "Global Brain" concept). The resulting synergy between previously competing individuals will release a lot of pent-up energy and creativity. This will solve all the problems of present society, which are caused by interpersonal and intrapersonal conflicts and by disregard for Nature.
Although the optimism of the "New Age" movement is appealing, and they certainly have a point when noting that many difficulties are caused by needless conflicts and contradictions, the methods they propose for transcending these problems appear rather naive. Their approach seems characterized by the absence of healthy scepticism. From science and technology they merely import metaphors, ignoring the hard work that goes into developing, testing and implementing new ideas. Basically, they propose that if people have enough goodwill, and sufficiently engage in consciousness-raising activities, like meditation and different forms of psychotherapy and "healing", the transition to the higher level, where all problems are solved, will occur automatically. This looks like wishful thinking more than like a concrete model of future developments.
A slightly more recent version of the doomsday scenario is the environmental holocaust. The main idea is that nuclear war, the uncontrolled proliferation of pollutants, and/or the exhaustion of natural resources have made the Earth all but uninhabitable. Civilisation has collapsed together with the ecosystem. The recurring image is that of a few gangs of survivers, together with mutant rats and cockroaches, fighting for the last remaining resources amongst the ruins of once proud cities. This pessimistic view too has recently become less popular. The reason is the much diminished likelihood of nuclear war, and the awareness that environmental problems, though serious, are being tackled more and more forcefully.
Cyberpunk
However, some processes grow even more quickly. For example, population growth in percentage per year is much larger now than it was a century ago. This is because medical progress has augmented the gap between the percentage of births and the percentage of deaths per year. If the growth of the world population over the past millenia is plotted out, the pattern appears to be hyperbolic rather than exponential. Hyperbolic growth is characterized by the fact that the inverse of the increasing variable (e.g. 1 divided by the total population) evolves according to a straight line that slopes downward. When the line reaches zero, this means that the variable (world population in this case) would become equal to 1 divided by zero, which means infinity. This is essentially different from an exponential growth process, which can never reach infinity in a finite time.
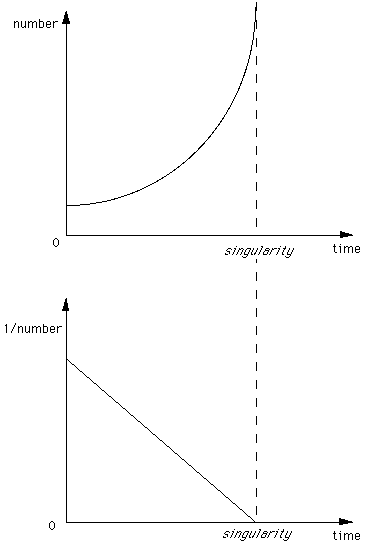
Fig. 1: a hyperbolic growth process, where the growing number becomes infinite in the singular point, while its inverse (1 divided by the number) becomes zero.
If the line describing the inverse of world population until recently is extended into the future, we see that it reaches zero around the year 2035. Of course, such an extrapolation is not realistic. It is clear that world population can never become infinite. In fact, population growth is slowing down at this moment. However, that slowdown itself is a revolutionary event, which breaks a trend that has persisted over all of human history.
In mathematics, the point where the value of an otherwise finite and continuous function becomes infinite is called a "singularity". Since traditional mathematical operations, like differentiation, integration and extrapolation, are based on continuity, they cannot be applied to this singular point. If you ask a computer to calculate the value of one divided by zero it will respond with an error message. A singularity can be defined as the point where mathematical modelling breaks down. The inside of a "black hole" is an example of a singularity in the geometry of space. No scientific theory can say anything about what happens beyond its boundary. We can only postulate that different laws will apply inside, but these laws remain forever out of sight. Similarly, the Big Bang, the beginning of the universe, is a singularity in time, and no amount of extrapolation can describe what happened before this singular event.
The mathematician and science fiction writer Vernor Vinge has proposed that
technological innovation is racing towards a singularity. Scientific discovery appears as an exponentially growing process with a
doubling period of about 15 years. However, the doubling period is
diminishing because of increasingly efficient communication and processing of
the newly derived knowledge. The rate of growth is itself growing. This makes
the process super-exponential, and possibly hyperbolic. Vinge would argue that
at some point in the near future the doubling period would reach zero, which
means that an infinite amount of knowledge would be generated in a finite time.
At that point, every extrapolation that we could make based on our present
understanding would become meaningless. The world will have entered a new
stage, where wholly different rules apply. Whatever remains of humanity as we
know it will have changed beyond recognition.
Some data supporting this conjecture can be found in a chart provided by Peter Peeters, in which the time elapsed between a dozen fundamental discoveries and their practical application is plotted against the year in which the invention was applied. The graph shows a downward sloping line, which reaches zero in the year 2000. These are just a few data points, and the implication that inventions will be applied virtually instantaneously after 2000 does not yet mean that scientific progress will be infinite. Vinge himself would situate the date of the singularity between 2010 and 2040. His reasoning is based on the accelerating growth of computer-aided intelligence. Rather than considering the IQ of an isolated individual, he would look at the team formed by a person and computer. According to Vinge, a PhD armed with an advanced workstation should already be able to solve all IQ tests ever devised. Since computing power undergoes a rapid exponential growth, we will soon reach the stage where the team (or perhaps even the computer on its own) would reach superhuman intelligence. Vinge defines this as the ability to create even greater intelligence than oneself. That is the point at which our understanding, which is based on the experience of our own intelligence, must break down.
A related reasoning was proposed by Jacques Vallée. Extrapolating from the phenomenal growth of computer networks and their power to transmit information, he noted that at some point all existing information would become available instantaneously everywhere. This is the "information singularity".
These models should not be taken too literally. They are metaphors, proposed to stimulate reflection. It does not make much sense to debate whether "the Singularity", if such a thing exists, will take place in 2029 or in 2035. Depending on the variable you consider most important, and the range over which you collect data points, you may find one date in which infinity is reached, or another, or none at all. Even if nothing as radical as a "New Age" could be predicted, the zero point method is certainly useful to attract the attention to possible crisis points, where the dynamics of change itself are altered. Peeters has used this method with some success to "predict" historical crises, such as the First World War and the 1930 and 1974 economic recessions. (The Second World War, strangely enough, did not seem to fit the model...).
The point to remember, however, is that abstract, non-material variables, such as intelligence, information, or innovation, aren't subjected to the same "limits to growth" which characterize the exhaustion of finite resources. Such variables could conceivably reach values which for all practical purposes may be called "infinite". Several parallel trends show a hyperbolic type of acceleration which seems to reach its asymptote (the point of infinite speed) somewhere in the first half of the 21st century. This does not mean that actual infinity will be reached, only that a fundamental transition is likely to take place. This will start a wholly new mode of development, governed by laws which we cannot as yet guess.
References:
Vernor Vinge on the Singularity
The technological singularity
Staring into the Singularity
As mentioned in section Social Evolution, the metasystem transition leading to human psychology and society also results in the emergence of a completely new level for the application of variation and selection, and of evolution itself, that of memetics and human culture. This is a turning point in the history of the world: the era of Reason begins. The human individual becomes a point of concentration of Cosmic Creativity. With the new mechanism of evolution, its rate increases manifold.
One of the implications of that transition concerns the interpretation of survival. In natural selection, the source of variation is the mutation of the gene; nature creates by experimenting on genes and seeing what kinds of bodies they produce. Therefore, nature has to destroy older creations in order to make room for the newer ones. In biological evolution survival means essentially survival of the genes, not so much survival of the individuals. With the exception of species extinction, we may say that genes are effectively immortal: it does not matter that an individual dies, as long as his genes persist in its offspring.
In socio-cultural evolution, the role of genes is played by memes, embodied in individual brains or social organizations, or stored in books, computers and other knowledge media. Thus the creative core of human individual is the engine of memetic evolution. In memetic evolution, memes must be immortal. While the mortality of multicellular organisms is necessary for biological evolution, it is no longer necessary for memetic evolution.
For the general purpose of evolution there is no more sense in killing humans. At the present new stage of evolution, the evolution of human-made culture, the human brain and its memetically based culture is the source of creativity, not an object of experimentation. Its loss in death is unjustifiable; it is an evolutionary absurdity. The immortality of human beings is on the agenda of Cosmic Evolution.
Most of the knowledge acquired by an individual still disappears at biological death. Only a tiny part of that knowledge is stored outside the brain or transmitted to other individuals. It is a shame to die before realizing one hundredth of what you have conceived and being unable to pass on your experience and intuition. It is a shame to forget things even though we know how to store huge amount of information in computers and access them in split seconds. Further evolution would be much more efficient if all knowledge acquired through experience could be maintained, in order to make place only for more adequate knowledge. This requires an effective immortality of the cognitive systems defining individual and collective minds: what would survive is not the material substrate (body or brain), but its cybernetic organization.
One way to reach this ideal has been called "uploading": the transfer of our mental organization to a very sophisticated computer system. Research in artificial intelligence, neural networks, machine learning and data mining is slowly uncovering techniques for making computers work in a more "brain-like" fashion, capable to learn billions of associated concepts without relying on the rigid logical structures used by older computer systems. See for example our research on learning, brain-like webs. If these techniques become more sophisticated, we might imagine computer systems which interact so intimately with a human use that they would "get to know" that user so well that they it could anticipate every reaction or desire. Since user and computer system would continuously work together, they would in a sense "merge": it would become meaningless to separate the one from the other. If at a certain stage the biological individual of this symbiotic couple would die, the computational part might carry on as if nothing had happened. The individual's mind could then be said to have survived in the non-organic part of the system.
Through such techniques, the form or organization with which we identify our "I" could be maintained infinitely, and, which is important, evolve, become even more sophisticated, and explore new, yet unthought of, possibilities. Even if the decay of biological bodies is inevitable, we can study ways of information exchange between bodies and brains which will preserve the essence of self-consciousness, our personal histories, our creative abilities, and, at the same time, make us part of a larger unity embracing, possibly, all of the humanity: the social superorganism. We call this form of immortality cybernetic, because cybernetics is a generic name for the study of control, communication, and organization. It subsumes biological immortality.
At present our ideas about cybernetic immortality are still abstract and vague. This is inevitable; long range notions and goals may be only abstract. But this does not mean that they are not relevant to our present concerns and problems. The concept of cybernetic immortality can give shape to the supreme goals and values we espouse, even though present-day people can think realistically only in terms of creative immortality (although -- who knows?). The problem of ultimate values is the central problem of our present society. What should we live for after our basic needs are so easily satisfied by the modern production system? What should we see as Good and what as Evil? Where are the ultimate criteria for judging social organization? Historically, great civilizations are inseparable from great religions which gave answers to these questions. The decline of traditional religions appealing to metaphysical immortality threatens to degrade modern society. Cybernetic immortality can take the place of metaphysical immortality to provide the ultimate goals and values for the emerging global civilization.
See further:
The integration of human beings will proceed in another dimension than that of human culture, a dimension of depth. We conceive of a realization of cybernetic immortality by means of very advanced human-machine systems, where the border between the organic (brain) and the artificially organic or electronic media (computer) becomes irrelevant. Such hybrid organisms would survive not so much through the biological material of their bodies, but through their cybernetic organization, which may be embodied in a combination of organic tissues, electronic networks, or other media. With communication through the direct connection of nervous systems to machines and to each other, the death of any particular biological component of the system would no longer imply the death of the whole system. Such metasystems will be evolutionary selective, in that they will have advantages for survival in an evolving environment. This is a cybernetic way for an individual human person to achieve immortality.
It is an open question whether such cybernetically immortal cognitive systems that would emerge after the next metasystem transition should be considered as individual beings ("meta-beings"), or as a society of beings (a ">super-being"). It is clear that the different levels have very complicated interactions in their effect on selection, and hence we need a careful cybernetic analysis of their mutual relations.
The creative act of free will is the "biological function" of the human being. In the integrated meta- or super-being it must be preserved as an inviolable foundation, and the new qualities must appear through it and because of it. Thus the fundamental challenge that the humanity faces now is to achieve an organic synthesis of integration and freedom.
The future immortality of the human person does not imply its frozen constancy. We can understand the situation by analogy with the preceding level of organization. Genes are controllers of biological evolution and they are immortal, as they should be. They do not stay unchanged, however, but undergo mutations, so that human chromosomes are a far cry from the chromosomes of viruses. Cybernetically immortal human persons may mutate and evolve in interaction with other members of the super-being, while possibly reproducing themselves in different materials. Those human persons who will evolve from us may be as different from us as we are different from viruses. But the defining principle of the human person will probably stay fixed, as did the defining principle of the gene.
Should we expect that the whole of humanity will unite into a single human super-being? This does not seem likely, if we judge from the history of evolution. Life grows like a pyramid; its top goes up while the basis is widening rather than narrowing. Even though we have seized control of the biosphere, our bodies make up only a small part of the whole biomass. The major part of it is still constituted by unicellular and primitive multicellular organisms, such as plankton. It is far from obvious that all people and all communities will wish to integrate into immortal super-beings. The will to immortality, as every human feature, varies widely in human populations. Since the integration we speak about can only be free, only a part of mankind --- probably a small part --- should be expected to integrate.
But it is the integrated part of humanity that will ultimately control the Universe. This becomes especially clear when we realize that the whole Cosmos, not just the planet Earth, is the arena for evolution. No cosmic role for the human race is possible without integration. The units that take decisions must be rewarded for those decisions, otherwise they will never take them. Can we imagine "human plankton" crowded in rockets in order to reach a distant star in ten, twenty or fifty generations? Only integrated immortal creatures can conquer the outer space.
Such initially vague analogies become more precise as the understanding of organisms increases. The concepts of systems theory provide a good framework for establishing a precise correspondence between organismic and societal functions. The fact that complex organisms, like our own bodies, are built up from individual cells, led to the concept of superorganism. If cells aggregate to form a multicellular organism, then organisms might aggregate to form an organism of organisms: a superorganism. Biologists agree that social insect colonies, such as ant nests or beehives, are best seen as such superorganisms. The activities of a single ant, bee or termite are meaningless unless they are understood in function of the survival of the colony.
Individual humans may seem similar to the cells of a social superorganism, but they are still much more independent than ants or cells (Heylighen & Campbell, 1995). This is especially clear if we look at the remaining competition, conflicts and misunderstandings between individuals and groups. Thus human society is still an ambivalent system, balancing between individual selfishness and collective responsibility. In that sense it may be more similar to organisms like slime molds or sponges, whose cells can live individually as well as collectively, than to true multicellular organisms. However, there seems to be a continuing trend towards global integration. As technological and social systems develop into a more closely knit tissue of interactions, transcending the old boundaries between countries and cultures, the social superorganism seems to turn from a metaphor into a reality.
Most recently, the technological revolution has produced a global communication network, which can be seen as a nervous system for this planetary being. As the computer network becomes more intelligent it starts to look more like a global brain or super-brain, with capabilities far surpassing those of individual people (see our page on learning, brain-like webs for an experimental approach to make the net more intelligent). This is part of an evolutionary transition to a higher level of complexity. A remaining question is whether this transition will lead to the integration of the whole of humanity, producing a human "super-being", or merely enhance the capabilities of individuals, thus producing a multitude of "meta-beings".
In order to study these different issues, the "Global Brain Group" has been created. Its members include most of the authors that have written on the subject. Their works and others are listed in the global brain bibliography).
Living Systems Theory, although I have left out some of the less important ones (e.g. timer), and added a few which seemed missing in Miller's list (e.g. "Immune System", "Energy carrier"). I have also renamed some functions to more traditional system terms (e.g. "sensor" instead of "input transducer"). I hope that the below correspondence shows that the "superorganism" model of human society is more than a vague metaphor, but rather an accurate framework for analysing the collectivity as a living system in its own right.
Example |
Organism
|
Society
|
| Units
|
Cells
|
People
|
| Differentiation
|
Tissue
types
|
Division
of labor
|
| Subsystems
|
Organs
|
Organizations
|
| Boundary
|
Skin
|
Walls,
Covers, ...
|
| Defenses
|
Immune
system
|
Army,
Police
|
Example |
Organism
|
Society
|
| Ingestor
|
eating,
drinking, inhaling
|
mining,
harvesting, pumping
|
| Converter
|
digestive
system, lungs
|
refineries,
processing plants
|
| Distributor
|
blood
circuit
|
transport
networks
|
| Energy
carrier
|
hemoglobin,
ATP
|
oil,
electricity
|
| Producer
|
cell
growth
|
factories,
builders
|
| Extruder
|
urine
excretion, defecation
|
waste
disposal, sewers, chimneys
|
| Storage
|
fat,
bones
|
warehouses,
containers
|
| Support
|
skeleton
|
buildings,
bridges...
|
| Motor
|
muscles
|
machines,
people, animals
|
Example |
Organism
|
Society
|
| Sensor
|
sensory
organs
|
reporters,
researchers
|
| Decoder
|
perception
|
experts,
politicians, public opinion
|
| Channel
and Net
|
nerves,
neurons
|
communication
media
|
| Associator
|
synaptic
learning
|
scientific
discovery, social learning
|
| Memory
|
neural
memory
|
libraries,
collective knowledge
|
| Decider
|
higher
brain functions
|
government,
market, voters
|
| Effector
|
nerves
activating muscles
|
executives
|
Reference: Heylighen F. (1997): "Towards a Global Brain. Integrating Individuals into the World-Wide Electronic Network", in: Der Sinn der Sinne, Uta Brandes & Claudia Neumann (Ed.) (Steidl Verlag, Göttingen) [in press]
intro and excerpt, including "Society is an organism")
Remarkable to note how many recently fashionable ideas about superorganisms and evolutionary integration have already been proposed by this evolutionary thinker over a century ago. Spencer coined the phrase "survival of the fittest", which was later taken over by Darwin.
Pierre Teilhard de Chardin:The Phenomenon of Man" (1959, Harper & Row, New York)).
the mystical and poetic vision of future evolutionary integration by this paleontologist and jesuit priest anticipates many recent developments. Teilhard popularized Vernadsky's term "
See also:
Joël de Rosnay: "L'Homme Symbiotique. Regards sur le troisième millénaire" (Seuil, Paris, 1996), "Le Cerveau Planétaire" (Olivier Orban, Paris, 1986), "Le Macroscope" (Seuil, Paris, 1972) (translated as: "The Macroscope", Harper & Row, New York, 1975)
emergence of the "
cybernetic theory of universal evolution, from unicellular organisms to culture and society, culminating in the emerging "super-being", based on the concept of the Metasystem Transition.
Peter Russell: "The Global Brain Awakens: Our next evolutionary leap" (Global Brain, 1996) (originally published in 1983 as "The Global Brain"). For an excerpt, see Towards a Global Brain
development of the superorganism theme in a "New Age" vision, with more emphasis on consciousness-raising techniques like meditation, and less on evolutionary mechanisms and technology.
Gottfried Mayer-Kress:several papers, including:
explores the analogies between global networks and complex adaptive systems, and the applications of the network to modelling complex problem domains
for a summary see:
"Metaman: the merging of humans and machines into a global superorganism", (Simon & Schuster, New York, 1993).Future Tech and Metaman, and Letter from the Editor)Center for the Study of Evolution and the Origin of Life (CSEOL) at UCLA in
Los Angeles.
an optimistic picture of the evolution of society, with many statistics on economic, social and technological progress, in which humans and machines unite, and where the individual is increasingly tied to others through technology
Brian R. Gaines:The Collective Stance in Modeling Expertise in Individuals and Organizations, International Journal of Expert Systems. 7(1), (1994), pp. 22-51. (see also The Emergence of Knowledge through Modeling and Management
Processes in Societies of Adaptive Agents.
(Proceedings of the 10th Knowledge Acquisition Workshop, Banff, Alberta.
pp. 24-1:24-13) and other Gaines articles)
an in-depth review of the literature on sociology, cognitive science and systems theory about the social function of knowledge; its "collective stance" views humanity as an organism partitioned into sub-organisms, such as organizations and individuals; proposes a positive feedback mechanism for the development of expertise, and therefore division-of-labor.
Selection of Organization at the Social Level: obstacles and facilitators of Metasystem Transitions, "World Futures: the journal of general evolution", Vol. 45:1-4 (1995), p. 181.
a critical examination of the evolutionary mechanisms underlying the emergence of social "superorganisms", like multicellular organisms, ant nests, or human organizations; concludes that humanity at present cannot yet be seen as a superorganism, and that there are serious obstacles on the road to further integration
discusses the precise mechanisms (learning, thinking, spreading activation, ...) through which a brain-like global network might be implemented, using the framework of the theory of metasystem transitions; see also learning, brain-like webs and Heylighen F. (1997): "Towards a Global Brain. Integrating Individuals into the World-Wide Electronic Network", in: Der Sinn der Sinne, Uta Brandes & Claudia Neumann (Ed.) (Steidl Verlag, Göttingen) [in press]
Ben Goertzel:World Wide Brain: The Emergence of Global Web Intelligence and How it Will Transform the Human Race
the concept of the WorldWideBrain as a massively parallel intelligence, consisting of structures and dynamics emergent from a community of intelligent WWW agents, distributed worldwide, with a discussion of social and philosophical implications, including a review of the discussions in the Global Brain Group; See also:
The Human Macro-organism as Fungus, Wired 4.04 (1996).
an intelligent parody of the superorganism view of society: "Pull Bill Gates out of his office and put him in the veldt - in four days he's a bloated corpse in the sun. ";-)
Lee Li-Jen Chen and Brian R. Gaines:A CyberOrganism Model for
Awareness in Collaborative
Communities on the Internet, International Journal of Intelligent Systems
(IJIS), Vol. 12, No. 1. pp. 31-56. (1997)
an awareness-oriented framework for the web, based on Miller's "Living Systems" theory and a collective intelligence model, to conceptualize the Internet as an organism; particular emphasis on tools for time awareness
Howard Bloom:The Lucifer Principle: A Scientific Expedition Into The Forces of History
a popular, non-academic book, which describes human social groups as superorganisms, whose members merge their minds into a single mass-learning machine; explores the manner in which our physiology renders us components of a superorganismic brain even in the absence of modern technology; see excerpt "
The Symbiotic intelligence project:Symbiotic Intelligence and the Internet.
George Pór:
The Quest for Collective Intelligence
: a practical approach inspired by systems ideas to the development of a "nervous system" for a community, viewed as a superorganism
The Evolution of the Social Brain (excerpts from the book "Continuum", Greenwich Publishers)
The Global Super-brain: connections with AI and philosophy
John Champagne's essay on "Gaia Brain"
Webmind project
Collective Intelligence and its Objects: Many-to-Many Communication in a 'Meaning World'
Alexander Chislenko has several relevant
essays, including Semantic Web - a vision of the future of intelligent Web, Networking in the Mind Age and Automated Collaborative Filtering and Semantic Transports
The global super-brain - A digital dream within an indifferent
society: a short master's thesis critically discussing the possibilities for collective
intelligence within the web
The group is associated with the Principia Cybernetica Project, and the Center "Leo Apostel". Membership is limited to people who have been doing active research and published books or papers on the subject. The present members are:
Joël de Rosnay (Cité des Sciences et de l'Industrie, Paris)
Peter Russell
Gottfried Mayer-Kress (Complex Systems, University of Illinois, Urbana-Champaign)
Center for the Study of Evolution and the Origin of Life, UCLA)
Ben Goertzel (Psychology Department, University of Western Australia)
Lee Li-Jen Chen (Computer Science, University of Calgary)
Computer Research and Applications Group, Los Alamos National Laboratory)
As a contact medium for the study group, an electronic mailing list has been created, gbrain@listserv.vub.ac.be (Global Brain Discussion). The list is private and was initially limited to group members, but participation has presently been extended to everyone whose submission is accepted by the group. (see the subscription form for joining the mailing list).
The mailing list is used to exchange information, references and ideas, and to discuss the main unsolved questions about the emergence of a global brain. The discussions can be consulted at the Web archive of the list.
Lycos), where one can type in several keywords and the engine selects those documents that contain a maximum of those keywords. E.g. the input of the words "pet" and "disease" might bring up documents that have to do with veterinary science. This only works if the document one is looking for effectively contains the words used as input. However, there might be other documents on the same subject using different words (e.g. "animal" and "illness") to discuss that issue. Here, again, spreading activation may help: documents about pets are normally linked to documents about animals, and so a spread of the activation received by "pet" to "animal" may be sufficient to select the searched-for documents. However, this assumes that the Web would be linked in an intelligent way, with semantically related documents (about "pets" and "animals") also being close in hyperspace. To achieve this we need a learning
However, this process would be much more efficient if it could work automatically, without anybody needing to manually create links. It is possible to implement simple algorithms that make the web learn (in real-time) from the paths of linked documents followed by the users. The principle is simply that links followed by many users become "stronger", while links that are rarely used become "weaker". Some simple heuristics can then propose likely candidates for new links, and retain the ones that gather most "strength". The process is illustrated by our "adaptive hypertext experiment", where a web of randomly connected words self-organizes into a semantic network, by learning from the link selections made by its users. If such learning algorithms could be generalized to the Web as a whole, the knowledge existing in the Web could become structured into a giant associative network which continuously adapts to the pattern of its usage.
Imagine the following situation: your dog is continuously licking mirrors. You don't know whether you should worry about that, or whether that is just normal behavior, or perhaps a symptom of some kind of disease. So you try to find more information by entering the keywords "dog", "licking" and "mirror" into a Web search. If there would be a "mirror-licking" syndrome described in the literature about dog diseases, such a search would immediately find the relevant documents. However, that phenomenon may just be an instance of the more general phenomenon that certain animals like to touch glass surfaces. A normal search on the above keywords would never find a description of that phenomenon, but the spread of activation in a semantically structured web would reach "animal" from "dog", "glass" from "mirror" and "touching" from "licking", thus activating documents that contain all three concepts. This example can be easily generalized to the most diverse and bizarre problems. Whether it has to do with how you decorate your house, how you reach a particular place, how you remove stains of a particular chemical, what is the natural history of the Yellowstone region: whatever the problem you have, if some knowledge about the issue exists somewhere, spreading activation should be able to find it.
For the more ill-structured problems, the answer may not come immediately, but be reached after a number of steps. Just like in normal thinking, formulating part of the problem brings up certain associations which may then call up others that make you reformulate the problem in a better way, which leads to a clearer view of the problem and again a more precise description and so on, until you get a satisfactory answer. The web will not only provide straight answers but general feedback that will direct you in your efforts to get closer to the answer.
The search process should not require you to select a number of search engines in different places of the Web. The new technology of net "agents" is based on the idea that you would formulate your problem or question, and that that request would itself travel over the Web, collecting information in different places, and send you back the result once it has explored all promising avenues. The software agent, a small message or script embodying a description of the things you want to know, a list of provisional results, and an address where it can reach you to send back the final solution, would play the role of an "external thought". Your thought would initially form in your own brain, then be translated automatically via a direct interface to an agent or thought in the external brain, continue its development by spreading activation, and come back to your own brain in a much enriched form. With a good enough interface, there should not really be a clear boundary between "internal" and "external" thought processes: the one would flow over naturally and immediately into the other.
Though individual people might refuse answering requests received through the super-brain, no one would want to miss the opportunity to use the unlimited knowledge and intelligence of the super-brain for answering one's own questions. However, normally you cannot continuously receive a service without giving anything in return. People will stop answering your requests if you never answer theirs. Similarly, one could imagine that the intelligent Web would be based on the simple condition that you can use it only if you provide some knowledge in return.
In the end the different brains of users may become so strongly integrated with the Web that the Web would literally become a "brain of brains": a super-brain. Thoughts would run from one user via the Web to another user, from there back to the Web, and so on. Thus, billions of thoughts would run in parallel over the super-brain, creating ever more knowledge in the process.
References:
Yet, even more direct communication between the human brain and the Web can be conceived. First, there have already been experiments (Wolpaw et al., 1991) in which people steer a cursor on a computer screen simply by thinking about it: their brain waves associated with particular thoughts (such as "up", "down", "left" or "right") are registered by sensors and interpreted by neural network software, which passes its interpretation on to the computer interface in the form of a command, which is then executed. Research is also being done on neural interfaces, providing a direct connection between nerves and computer. (see also Gregory Kovacs's Neural Interface Project)
Once these technologies have become more sophisticated, we could imagine the following scenario: at any moment a thought might form in your brain, then be translated automatically via a neural interface to an agent or thought in the external brain, continue its development by spreading activation, and come back to your own brain in a much enriched form. With a good enough interface, there should not really be a border between 'internal' and 'external' thought processes: the one would flow naturally and immediately into the other.
See Also:
The Brain-Computer Interface: Techniques for Controlling Machines
We can distinguish two levels of cybernetic systems involved in the global brain:
This problem is well known. The reason why it is not yet solved is simply that the problem is immensely difficult. Practical people get satisfied with partial solutions: creation of narrowly specialized sublanguages which superficially look like human languages. Financing of more ambitious projects is tight, because nobody can promise fast returns on this path.
Why is our philosophy relevant?
Developing a universal semantic language we must start with some elements which are absolutely minimal and primitive, so that all representations that are involved in human laguages could be expressed in terms of our semantic language as constructions from those primitive elements. Otherwise it is hardly possible to obtain the formality that is demanded by the computer.
Our ontology states that such primitive elements are actions, and nothing but actions, while objects are relation between actions. Our epistemology states that the meaning of linguistic statements is in the predictions they produce. But the concept of a prediction takes us, again, to the action whose termination it states. The other kind of linguistic objects, commands return us even more directly to actions. Thus we have a closed basis for a formal system.
So, why not try? Any ideas and accounts of relevant work are welcome. Representation of semantics on the basis of formal logic and some primitive predicates, which is used in much work on artificial intelligence, is, certainly, relevant. Our goal should be going further down in analysis than it is usually done -- a goal that requires a consistent and all-embracing philosophy.
However, we must take into account the principle of natural selection, which implies that if our goals are incompatible with the conditions necessary for survival, then we will be eliminated from the natural scene. Of course, there is no natural law or absolute moral principle which forbids you to commit suicide, but you must be aware that this means that the world will continue without you, and that it will quickly forget that you ever have been there. If we wish to evade this alternative, this means that we will have to do everything for maximising survival.
A second fallacy to avoid is the naive extrapolation of past evolution into the present or future. The mechanisms of survival and adaptation that were developed during evolution contain a lot of wisdom--about past situations (Campbell, 1978). They are not necessarily adequate for present circumstances. This must be emphasized especially in view of the creativity of evolution: the emergence of new levels of complexity, governed by novel laws.
For example, biological evolution, based on the survival of the genes, has favoured selfishness: maximizing one's own profit, with a disregard for others (unless those others carry one's own genes: close family). In a human society, on the other hand, we need moral principles that promote cooperation, curbing too strong selfishness. Once the social interactions have sufficiently developed the appearance of such moral principles (e.g. "thou shalt not steal") becomes advantageous, and hence will be reinforced by natural selection, even though it runs counter to previous "selfish" selection mechanisms (Campbell, 1978). The development of human society is an example of a metasystem transition, which creates a new system evolving through a mechanism which is no longer genetical but cultural (Turchin, 1977).
One of the implications of that transition concerns the interpretation of survival. Although the death of individual organisms may increase genetic fitness, by concentrating resources on reproduction rather than survival of the individual (see the evolutionary causes of death), it does not benefit cultural evolution. In biological evolution survival means essentially survival of the genes, not so much survival of the individuals (Dawkins, 1976). With the exception of species extinction, we may say that genes are effectively immortal: it does not matter that an individual dies, as long as his or her genes persist in off-spring. In socio-cultural evolution, the role of genes is played by cognitive systems ("memes"), embodied in individual brains or social organizations, or stored in books, computers and other knowledge media. However, most of the knowledge acquired by an individual still disappears at biological death. Only a tiny part of that knowledge is stored outside the brain or transmitted to other individuals. Further evolution would be much more efficient if all knowledge acquired through experience could be maintained, in order to make place only for more adequate knowledge.
This requires an effective immortality of the cognitive systems defining individual and collective minds: what would survive is not the material substrate (body or brain), but its cybernetic organization. This may be called "cybernetic immortality" (Turchin, 1991). We could conceive its realization by means of very advanced man-machine systems, where the border between the organic (brain) and the artificially organic or electronic media (computer) becomes irrelevant. The death of a biological component of the system would no longer imply the death of the whole system.
Cybernetic immortality can be conceived as an ultimate goal or value, capable to motivate long-term human action. It is in this respect similar to metaphysical immortality (Turchin, 1991): the survival of the "soul" in heaven promised by the traditional religions in order to motivate individuals to obey their ethical teachings (Campbell, 1979), and to creative immortality (Turchin, 1991): the driving force behind artists, authors or scientists, who hope to survive in the works they leave to posterity.
Another basic value that can be derived from the concept of survival
is "self-actualization" (Maslow, 1970): the desire to actualize
the human potential, that is to say to maximally develop the knowledge,
intelligence and wisdom which may help us to secure survival for all future
contingencies. Self-actualization may be defined as an
optimal, conscious use of the variety of actions we are capable to execute.
However, if that variety becomes too great, as seems to be the case in our present, extremely complex society, a new control level is needed (Heylighen, 1991b). This may be realized by a new metasystem transition, leading to a yet higher level of evolution. A more detailed understanding of this next transition may help us to answer the question "Where are we going to?", that is to say to understand the future of evolution.
The main remaining problem of an evolutionary ethics is how to reconcile the goals of survival on the different levels: the level of the individual (personal freedom), the society (integration of individuals), and the planet (survival of the world ecology as a whole). It is an open question whether the "cybernetically immortal" cognitive system that would emerge after the next metasystem transition would be embodied most effectively in an individual being ("metabeing"), or in a society of individuals ("superbeing"). It is clear that the different levels have very complicated interactions in their effect on selection (Campbell, 1979), and hence we need a careful cybernetic analysis of their mutual relations. The necessary competition between levels follows from the problem of suboptimization, according to which what is best for a subsystem is in general not best for the global system.
References
Campbell D.T. (1979): "Comments on the sociobiology of ethics and moralizing", Behavioral Science 24, p. 37-45.
Dawkins R. (1976): The Selfish Gene, (Oxford University Press, New York).
Heylighen F. (1991): "Evolutionary Foundations
for Metaphysics, Epistemology and Ethics", in : Workbook
of the 1st Principia Cybernetica Workshop, Heylighen F. (ed.) (Principia
Cybernetica, Brussels-New York), p. 33-39.
Maslow A. (1970): Motivation and Personality (2nd ed.), (Harper & Row, New York).
Turchin V. (1991): "Cybernetics and Philosophy", in: Proc.
8th Int. Conf. of Cybernetics and Systems, F. Geyer (ed.), (Intersystems,
Salinas, CA).
Turchin, V. (1977): The Phenomenon of Science, (Columbia University Press, New York ).
Goals of organized systems form a hierarchy. When two diffe rent goals come into confilct, we call for a higher goal, or a principle, or a value, which we choose to resolve the conflict. The thing which interests us at most today is the highest of these principles: the Supreme Goal, or the Supreme Value of human life. This is the problem of ethics. Philosophy and religion work on this problem traditionally. How does it look from the scien tist's point of view?
The first attempt of an answer leads to a discouraging result. Science is alien to ethics by its very essence. It ans wers only to the questions of how things are, but not how they ought to be. It does not say what is good and what is bad. As an American philosopher remarked, no matter how carefully you study the railroad schedule, you will not find there an indication where you want to go.
It is thinkable, however, that science could kill ethics as an independent subject. For somebody who lived in the 19th centu ry and took seriously and consistently the implications of the science of his time, like Karl Marx did, it was quite natural to believe that the problem of ethics was not real, but imagined.
In the nineteenth century the picture of the world given by science was broadly as follows. Very small particles of matter move about in virtually empty three-dimensional space. These particles act on one another with forces which are uniquely determined by their positioning and velocities.The forces of interaction, in their turn, uniquely determine, in accordance with Newton's laws, the subsequent movement of particles. Thus each subsequent state of the world is determined, in a unique way, by its preceding state. Determinism was an intrinsic feature of the scientific worldview of that time. In such a world there was no room for freedom: it was illusory. Humans, themselves merely aggregates of particles, had as much freedom as wound-up watch mechanisms.
With this worldview, the problem of ethics is not to decide what is good and what is evil, but simply to predict how people will behave in given circumstances. It is only a branch of sci ence, the science of behavior. This trend of thinking was the thoeretical basis for the Marxist economic determinism, and the Leninist totalitarianism which brought misery and dehumanisation to millions, if not billions of people. In the twentieth century the scientific worldview has undergone a radical change. It has turned out that subatomic physics cannot be understood within the framework of the Naive Realism of the nineteenth century scientists. The theory of Relativity and, especially, Quantum Mechanics require that our worldview be based on Criti cal Philosophy, according to which all our theories and mental pictures of the world are only devices to organize and foresee our experience, and not the images of the world as it "really" is. Thus along with the twentieth-century's specific discove ries in the physics of the microworld, we must regard the inevi tability of critical philosophy as a scientific discovery -- one of the greatest of the twentieth century.
We now know that the notion that the world is "really" space in which small particles move along definite trajectories, is illusory: it is contradicted by experimental facts. We also know that determinism, i.e. the notion that in the last analysis all the events in the world must have specific causes, is illusory too. On the contrary, freedom, which was banned from the science of the nineteenth century as an illusion, became a part, if not the essence, of reality. The mechanistic world-view saw the laws of nature as something that uniquely prescribes how events should develop, with indeterminacy resulting only from our lack of knowledge; contemporary science regards the laws of nature as only restrictions imposed on a basically non-deterministic world. There is genuine freedom in the world. When we observe it from the outside, it takes the form of quantum-mechanical unpredictability; when we observe it from within, we call it our free will. We know that the reason why our behaviour is unpre dictable from the outside is that we have ultimate freedom of choice. This freedom is the very essence of our personalities, the treasure of our lives. It is given us as the first element of the world we come into. Logically, the concept of free will is primary, impossible to derive or to explain from anything else. The concept of necessity, including the concept of a natural law, is a derivative: we call necessary, or predetermined, those things which cannot be changed at will.
Thus the modern philosophy of science leaves ethics separate from science, and, of course, extremely important, because the kind of life we have depends on the kind of goals we set. Science gives us knowledge, but does not immediately direct our will. The gap separating knowledge and will can never be fully bridged. It is true -- and important -- that knowledge can direct will, make certain decisions natural, highly probable or almost inevitable. But there is no necessity on the path from knowledge to action. With any given knowledge we are still free to set any goal at will. Goals can be logically derived only from goals, not from knowledge.
Then is there any way in which science is relevant to ethics? I believe there is. The link between the two is provided by the concept of evolution, and by the inborn feature of human beings which I call the will for immortality.
The distinction between knowledge and will can also be mapped into another perennial issue in ethics, that between ends (what to do: values, desires, goals) and means (how it can be done: beliefs, knowledge). Just as it is a truism that the ends cannot justify the means, so it is that the means cannot choose the ends.
The theory of ethics recognizes goals as values, or what is good. Philosophical ethics has long been aware of this split as we describe it between knowledge and values. There have been many attempts to search for a "primary value", from which the others can be derived. God's will has been suggested as a theological source of such a value. This we must reject as non-physicalist and non-constructive. An alternative ethical theory relies on naturalism (what is, is good).
A logical approach considers what combinations of goals will result in stable systems. The culmination of this approach is Kant's categorical imperative, which states that only actions which can be universally generalized to all actors can be ethical. Thus murder is unethical since universal generalization (universal murder) results in a lack of victims to further murder.
Our approach is developed from the conceptual basis outlined above, and is a combination of the last two approaches. While primary values cannot be derived from nature, they must be consistent with evolution and natural selection which is based on survival. Thus we take survival, in the most general sense, as the primary value. Because of the "Red Queen Principle" the seemingly conservative value of survival necessarily entails continuing progress, development, or growth. Thus we can from there derive the ultimate good as the continuation of the process of evolution itself, avoiding evolutionary "dead ends" and general extinction.
| Synopsys: |
The utilitarians have posited the basic value or goal that society should strive for as "the greatest happiness for the greatest number". However, how to create such happiness remains one of the eternal philosophical questions. Different philosophers have proposed the most diverse answers to that question. The only thing most of these answers seem to have in common is that they are so vague or ambiguous that you cannot test them out in practice. Insofar that some of these utopian views of the ideal society or way of life have been realized, for example in communism, they have generally turned out to be disastrously wrong.
Our evolutionary-cybernetic philosophy, on the other hand, proposes an answer which seems both theoretically well-founded and in good agreement with psychological and sociological observations of the factors that correlate with happiness. We will first sketch the theoretical argument, then review the empirical evidence.
We can define momentary happiness as pleasant feeling or the subjective experience of well-being. Long term happiness then corresponds to the preponderance of pleasant feelings over a prolonged period. This corresponds to the degree to which people feel satisfied with their life as a whole. Though not exactly the same, this sense of happiness is nearly synonymous with life-satisfaction, quality-of-life, or even "self-actualization" (Heylighen, 1992).
An evolutionary theory of happiness must clarify the connection between the objective property of fitness and the subjective experience of feeling well. Biologically, feelings function to orient an organism away from dangerous situations (signalled by unpleasant affects such as fear, hunger or pain), and towards positive situations (signalled by positive affects, such as enjoyment, love, satisfaction). Thus, feelings play the role of vicarious selectors: they select appropriate actions, such as drinking when thirsty, and reject inappropriate actions, such as touching a flame, thus substituting for natural selection. Therefore, positive feelings will normally indicate that the organism is approaching the optimal state.
Happiness can therefore be seen as an indication that a person is biologically fit (near to the optimal state) and cognitively in control (capable of counteracting eventual deviations from that optimal state), in other words that he or she can satisfy all basic needs, in spite of possible perturbations from the environment. Such control over one's situation has three components (Heylighen, 1992):
World Database of Happiness, collecting the results of hundreds of studies in which people were asked how happy or how satisfied they are with their life. Veenhoven (1991, 1995) then studied the main factors that correlate with the resulting happiness scores. His first conclusion is that happiness is not relative or dependent on a purely subjective outlook, as some theories posit. Indeed, happiness can be rather accurately predicted on the basis of the objective "liveability" of the society in which the individual lives, and on the basis of his or her personal profile. Let us discuss the factors that have strong positive correlations with happiness. We will begin with the characteristic of societies where people tend to be
happy:
References:
A Cognitive-Systemic Reconstruction of Maslow's Theory of Self-Actualization", Behavioral Science 37, p. 39-58.
The principle of suboptimization can be derived from the more basic systemic principle stating that "the whole is more than the sum of its parts". If the system (e.g. the wolf pack) would be a simple sum or "aggregate" of its parts, then the outcome for the system as a whole (total prey killed) would be a sum of the outcomes for the parts (prey killed by each wolf separately), but that is clearly not the case when there is interaction (and in particular cooperation) between the parts. Indeed, a pack of wolves together can kill animals (e.g. a moose or a deer), that are too big to be killed by any wolf in separation. Another way of expressing this aspect of "non-linearity" is to say that the interaction the different wolves are engaged in is a non zero-sum game, that is, the sum of resources that can be gained is not constant, and depends on the specific interactions between the wolves.
As a last example, suppose you want to buy a new car, and you have the choice between a normal model, and a model with a catalyser, that strongly reduces the poisonous substances in the exhaust. The model with catalyser is definitely more expensive, but the advantage for you is minimal since the pollution from your exhaust is diffused in the air and you yourself will never be able to distinguish any effect on your health of pollution coming from your own car. Rational or optimizing decision-making from your part would lead you to buy the car without catalyser. However, if everybody would make that choice, the total amount of pollution produced would have an effect on everybody's health, including your own, that will be very serious, and certainly worthy the relatively small investment of buying a catalyser. The suboptimizing decision (no catalyser) is inconsistent with the globally optimizing one (everybody a catalyser). The reason is that there is interaction between the different subsystems (owners and their cars), since everybody inhales the pollutants produced by everybody. Hence, there is also an interaction between the decision problems of each of the subsystems, and the combination of the optimal decisions for each of the subproblems will be different from the optimal decision for the global problem.
The problem of suboptimization underlies most of the problems appearing in evolutionary ethics. Indeed, ethics tries to achieve the "greatest good for the greatest number", but the greatest good (optimal outcome) for an individual is in general different from the greatest group for a system (e.g. society) of individuals.
Reference: Heylighen F. (1992) : "Evolution,
Selfishness and Cooperation", Journal of Ideas, Vol 2, # 4, pp
70-76.
| Action of A\Action of B | Cooperate | Defect |
| Cooperate | Fairly good [+ 5] | Bad [ - 10] |
| Defect | Good [+ 10] | Mediocre [0] |
Such a distribution of losses and gains seems natural for many situations, since the cooperator whose action is not returned will lose resources to the defector, without either of them being able to collect the additional gain coming from the "synergy" of their cooperation. For simplicity we might consider the Prisoner's dilemma as zero-sum insofar as there is no mutual cooperation: either each gets 0 when both defect, or when one of them cooperates, the defector gets + 10, and the cooperator - 10, in total 0. On the other hand, if both cooperate the resulting synergy creates an additional gain that makes the sum positive: each of them gets 5, in total 10.
The gain for mutual cooperation (5) in the prisoner's dilemma is kept smaller than the gain for one-sided defection (10), so that there would always be a "temptation" to defect. This assumption is not generally valid. For example, it is easy to imagine that two wolves together would be able to kill an animal that is more than twice as large as the largest one each of them might have killed on his own. Even if an altruistic wolf would kill a rabbit and give it to another wolf, and the other wolf would do nothing in return, the selfish wolf would still have less to eat than if he had helped his companion to kill a deer. Yet we will assume that the synergistic effect is smaller than the gains made by defection (i.e. letting someone help you without doing anything in return).
This is realistic if we take into account the fact that the synergy usually only gets its full power after a long term process of mutual cooperation (hunting a deer is a quite time-consuming and complicated business). The prisoner's dilemma is meant to study short term decision-making where the actors do not have any specific expectations about future interactions or collaborations (as is the case in the original situation of the jailed criminals). This is the normal situation during blind-variation-and-selective-retention evolution. Long term cooperations can only evolve after short term ones have been selected: evolution is cumulative, adding small improvements upon small improvements, but without blindly making major jumps.
The problem with the prisoner's dilemma is that if both decision-makers were purely rational, they would never cooperate. Indeed, rational decision-making means that you make the decision which is best for you whatever the other actor chooses. Suppose the other one would defect, then it is rational to defect yourself: you won't gain anything, but if you do not defect you will be stuck with a -10 loss. Suppose the other one would cooperate, then you will gain anyway, but you will gain more if you do not cooperate, so here too the rational choice is to defect. The problem is that if both actors are rational, both will decide to defect, and none of them will gain anything. However, if both would "irrationally" decide to cooperate, both would gain 5 points. This seeming paradox can be formulated more explicitly through the principle of suboptimization.
See also:
interactive implementation of the Prisoner's dilemma where you can play the game yourself
review
Evolution,
Selfishness and Cooperation", Journal of Ideas, Vol 2, # 4, pp
70-76.
See the memetic scenarios for evolving cooperation.
Living creatures display a behavior resulting from having both knowledge and goals. Both knowledge and goals are organized hierarchically. Similarly, in order to achieve a higher-level goal the system has to set and achieve a number of lower-level goals (subgoals). This hierarchy has a top: on the one hand, the limits of a creature's ultimate knowledge; on the other, the supreme, ultimate goals, or ultimate value, of a creature's life. As discussed in section philosophy, philosophy results as we consider the top of the hierarchy of knowledge, the deepest questions. In a non-human animal this top is inborn: the basic instincts of survival and reproduction. In a human being the top goals can go beyond animal instincts.
Ultimate human knowledge is science. But since an essential property of human intelligence is people's ability to control their goal setting, the ultimate human freedom is to choose our highest goals, our "meaning of life", and our ethics. Evolutionary ethics got a bad reputation because of its association with the "naturalistic fallacy": the mistaken belief that human goals and values are determined by, or can be deduced from, natural evolution. Values cannot be derived from facts about nature: ultimately we are free in choosing our own goals.
The supreme goals, or values, of human life are, in the last analysis, set by an individual in an act of free choice. This produces the historic plurality of ethical and religious teachings. There is, however a common denominator to these teachings: the will to immortality. The animal is not aware of its imminent death; the human person is. The human will to immortality is a natural extension of the animal will for life.
Since the newest mechanism of evolution is inside individual people, the will to immortality is now not only desirable, but also evolutionarily demanded. Since ultimate goals cannot be derived, only chosen, it is not possible to justify the will to immortality as the ultimate goal for people, or to assert it as dogma, as traditional religions do. Rather it must be the free, creative act of each individual.
Every human being experiences a moment in his/her life, usually in childhood, when he clearly realizes for the first time that sooner or later he will die -- inevitably. This comes as a shock. You feel that you are cornered, and there is no way out. Your imagination jumps over the years you have still to live through, and you find yourself on the brink of disappearance, complete annihilation. You realize that you are, essentially, on the death row. Different individuals react to this situation with different degree of acuteness. Some try simply forget about it, and succeed, to some degree. Others try forget but cannot. Life seems to have no point, because all roads lead to annihilation; one is haunted by the feeling that whatever he is doing is in vain.
This is a very ancient feeling. Remember the book of Eccleseastis. We can be sure, though, that the feeling is much more ancient than the Bible. The realization of one's own mortal nature is a most fundamental distinctions between a human being and an animal. Rebellion against death is found at the source of religions, philosophies, and civilizations. People look for a way to transcend the limit put on our lives by nature. They look for a concept which would reconcile the impulse to live on, which is inherent to every healthy creature, with the inevitability of death. Some concept of immortality becomes necessary for keeping life meaningful.
See also: Immortality and Life Extension
The theory of evolution is the cornerstone of the contemporary scientific worldview. Evolution is a constant emergence of higher and higher levels of cybernetic control. This process provides a material means for the manifestation of the mysterious something that we call freedom, or will, or free will. Evolution proceeds by metasystem transitions, in which a number of pre viously uncoordinated systems become controled by a metasystem, which thereby vastly expands the effects of its free choices. Hierarchical levels of control created by evolution are, essentially,amplifiers of freedom.
The evolutionary growth of the control hierarchy is a natural law, to which we refer as the Law of Evolution, or the Plan of Evolution. Like every law of nature, the Plan of Evolution does not determine uniquely and in detail how things will develop. It only sets the boundaries between the possible and the impossible. But it introduces a new dimension into the world, which provides a basis for distinguishing between good and evil. No one has proved, and hardly will ever prove, that the existence of life, and specifically, highly organized life, is inevitable. We have not yet had any sign that life exists outside Earth; as for humankind, it can destroy itself, and possibly the whole of life, if it chooses to do so. Continuing constructive evolution is a possibility but not a necessity. Acts of will can contribute to evolution or counter it. Because of the natureof evolution, there is a fundamental difference between constructive and destructive contributions.
The fate of the world is not predetermined, it depends, among other things, on what I and you are doing. The contribution to the Evolution made by an individual can be of critical importance. It can also be everlasting. For example, the contribution made by Aristotle or Newton is written down into the history of mankind and will stay there forever, even though there are only very few people who read Aristotle or Newton now. But each next stage of evolution is dependent on the preceding stages. The acts contributing to evolution create structures which will outlive the actors and determine the structures that follow. In this way, they are eternal. Those acts which go against the plan of evolution will be drowned in chaos and erased from the memory of the world. Evolutionary immortality is the immortality of deed. The deeds of mortal men may be immortal.
You can say that this evolutionary immortality is rather pale, not real. But it is quite real, especially for imaginative and creative people. The reason why we appreciate creative per sons -- sometimes even deify them -- is that we understand the eternal nature of their contributions. For creative persons it is important that their achievements are known and used, i.e. that they make a difference, and in this way stay forever. It may become more imortant than life itself. You know the famous story about Archimedes who said to the Roman soldier: you can kill me but please do not destroy my drawings. Even if this story is invented, which is quite possible, it still is very telling.
Speaking specifically, however, about the form of life of which we are part, it is not clear whether it is possible to modify it in such a way that our bodies become immortal. Contemporary biology does not give, as yet, a definite answer to this question. It is possible that the mechanism of aging is built-in on such a deep level, that you cannot switch it off without radically altering the whole machinery of bodily life. And there are still chances of an accidental death, which become the more serious the longer we live. This is another reason of being skeptical about biological immortality. The third reason is that an infinite extension of biological life, if it is not accompanied by some kind of development, evolution, is hardly attractive. Just imagine that you have to live eternally, really eternally, repeating the same cycle of actions and feelings, again and again. To me this looks as a nightmare. Because of these reasons I believe that in order to become immortal we must go beyond our present form of life. This brings us to the last, and the most modern, concept of immortality: cybernetic immortality.
See also:
Life-extension: a collection of links and notes on methods for living longer
and Life Extension
The project is managed by an editorial board, which is responsible for the production, maintenance and selection of the material. Everybody interested can contribute to the material being developed. Editors and contributors together use various methods of collaboration, mostly through the new electronic media of cyberspace.
Direct discussions among the contributors, and announcements of new developments, take place on the PRNCYB-L and PCP-news electronic mailing lists. The results produced by the project are maintained and made publically available on two information servers:
Although most of the collaboration takes place electronically, PCP also deploys more traditional academic activities, such as the organization of conferences and the publication of books or articles in scientific journals. This again ensures the accessibility of PCP's results to people who are not yet capable of using the new electronic media. The editors try in general to make the project's results publically known, especially in the hope of attracting new contributors, and they are interested in the different reactions elicited by the project, so that they may correct mistakes or wrong impressions.
For a list of names and addresses of the people involved and the different services provided, check the project's masthead.
Activities: PCP publishes electronic texts and facilitates scholarly work via its World-Wide Web server, Principia Cybernetica Web, electronic mailing lists, and through conferences and traditional publications.
Copyright: Unless stated otherwise, all electronic texts are Copyright ©1992-1998 Principia Cybernetica. Limited permission is granted for copying (see full copyright statement).
Participation: Participation by the community in all aspects of the project is solicited. Submit proposals to the Editorial Board.
Development of Principia Cybernetica is seen as a long term project involving many participants. It will be managed by a Board of Editors, who are responsible for implementation of the system and the collection and development of the material. Similar to a journal, it may rely on an Editorial Advisory Board, and other associated editors, referees, and contributors.
Thus Principia Cybernetica is seen as necessarily open ended and developing, essentially a process of discourse among a community of researchers. A variety of collaboratory granularities are possible, ranging from contributions by individual authors, through groups of authors, to consensual statements of all project participants.
Participants are free to develop their material within Principia Cybernetica while having it simultaneously available for traditional publications. Copyright is initially held by Principia Cybernetica, which then liberally grants permission for external publication. Thus traditional publication of parts or the whole of the network by individual authors or groups of authors will be made periodically.
These principles can be applied not only to physical or biological systems, but also to ideas: concepts and systems of concepts. (Ideas that are replicated when they are communicated from one person to another one are called "memes".) These principles are constructive, in the sense that they assume a variety of "primitive" systems (e.g. nodes containing expositions written by diverse participants), which undergo different combinations and recombinations (e.g. connection through hypertext links), and finally selection, so as to retain those nodes or combinations of nodes which are most "fit". There will be a development of higher levels of organization through the combination of simpler subsystems into supersystems. We foresee metasystem transitions occurring within the body of the Principia Cybernetica Web itself, perhaps in a manner similar to that of metasystem transitions in formal systems. The basic methodology for quickly developing a knowledge system as complex as a cybernetic philosophy would consist in supporting, directing and amplifying this natural development with the help of different cybernetic technologies and methods.
It will require, first, a large variety of concepts or ideas, provided by a variety of sources: different contributors to the project with different scientific and cultural backgrounds. The easy gathering, exchange, editing and otherwise manipulating of these ideas by a group of contributors can be facilated by different techniques from computer-supported cooperative work.
The knowledge system we are trying to build will be structured like a semantic network: the meaning of a node should be entailed by the links it has with other nodes. Determining an unambiguous meaning for each node requires a thorough semantic analysis. However, one must keep in mind that it is generally impossible to completely represent any concept's meaning: meanings are always to some degree context-dependent and any formal definition can only be temporary and approximate. First-order, coarse approximations can in a later stage perhaps be replaced by more precise approximations, in a bootstrapping fashion. We call this process progressive formalization. Determining meanings of concepts also requires reaching a consensus between the collaborators. This can be achieved through a process similar to the scientific method of peer-reviewed publication under the guidance of an editorial board.
Implicit consensus, however, can also be used to experiment with a process of spontaneous self-organization of the semantic network: the more people agree that two concepts should be directly linked, the stronger the link will become. The semantic analysis too can be supported by an autonomous process: by checking the similarities and differences in linking patterns, such a program could suggest different ways of restructuring the network, so as to make it semantically more simple and coherent.
See also: Links on Computer-Supported Collaborations
The first difficulty with the practical development of a Principia Cybernetica is that something as large and as complex as a full cybernetic philosophy, integrating all the different scientific disciplines and domains of human endeavour, cannot be elaborated by a few individuals. We clearly need a large variety of contributors from many different backgrounds (the traditional scientific disciplines, but also e.g. philosophy, technology, religion, art, ...). These people will typically be scattered over many geographic regions, countries, or even continents. The only way for them to collaborate efficiently is by means of the new telecommunication media (Joslyn, 1990).
Though we could imagine the exchange of information by the more traditional mail and the publication of journals or newsletters, these printed media are very slow with respect to the amount of information exchange that is to be done. In midterm future we may expect the development of broadband ISDN: the Integrated Services Digital Network, which would provide immediate electronic communication through all different media: text, sound, images, and even video. Though we cannot rely on this in the present situation, we can already start with the practically functioning electronic media of today: fax and electronic mail. Especially electronic mail (email), which allows the almost immediate transmission of electronic text files at virtually no cost between different continents, is directly useful for our project (Joslyn, 1990). Fax, though it is presently much more widespread, has the disadvantage that is does not provide a format for storing texts on computer, but with the spreading of optical character recognition and the integration of fax and computer, we may expect that both media will be interconnected in the very near future.
The communication of text files through computers allows much more than just a faster exchange of letters: it offers a whole array of techniques for electronic publishing (Gardner, 1990). The simplest of those is the "mailing list": a computer stores a list of addresses of people interested in the same subject. Every message that is sent to the computer by one of those people is (possibly after evaluation by a list administrator) sent further to all others on the list. This is a more dynamic form of a newsletter, where everybody can read the information almost immediately after it was written. It allows much more direct discussion than the traditional printed media. In first instance the Principia Project would be implemented through such a mailing list, similar to the list on Cybernetics and Systems (CYBSYS-L) which already exists at the SUNY-Binghamton computer center. People who do not as yet dispose of electronic mail facilities could in a preliminary stage send their contributions to an intermediary who would convert their telexed, faxed or posted messages to email. The main contributions received on the electronic list would be redistributed in a printed form through a traditional newsletter which can also be read by people without email connection.
Electronic publishing offers even more facilities. For example all information received on the list could be stored somewhere on a central computer, and everybody connected to the network could require specific information from this "file server". In this way the whole body of knowledge gathered to date can be selectively consulted by all people involved in the project.
Traditional collaboration is necessarily sequential: one individual can only add something after another one has finished. This even applies to real-time meetings or conversations: only one person can talk at a time. In a CSCW environment, on the other hand, people can add information in parallel. Moreover, the collaboration is not restricted to real-time or other physical constraints depending on time or space. The different people collaborating need not be present in the same location or even at the same time. The simplest way to implement this kind of asynchrous and distributed shared workspace is through annotation: different collaborators can add comments to specific parts of a collective document. This is implemented over the World-Wide Web in the Principia Cybernetica Project, thus abolishing all geographical constraints.
Moreover, CSCW makes it possible to overcome or control for a number of social constraints: in normal meetings, people who are assertive, fluent or in a position of authority will tend to dominate the discussion, while those who are shy or of a lower rank will find it very difficult to have their ideas accepted or even paid attention to, however good those ideas may be. In a CSCW environment, everyone types at his own speed or in his own style, without needing to wait until the others given him or her the occasion to speak. Moreover, through the use of nicknames or other devices the contributors can be kept anonymous so that the idea of the general manager is considered with the same unbiased attitude as the one of the junior employee. Using the public Internet as communication medium makes it even possible to maximally open up the group of collaborators, and allow virtually every person in the world to participate.
Finally, the inherent computing capabilities of CSCW tools make it possible to overcome cognitive constraints, by processing information that would be too complex to use in traditional environments. For example, different alternatives could be evaluated according to different criteria, whereby each collaborator could give his personal estimate along each of several dimensions. Statistical techniques from Multi-Criteria Decision Analysis can then be used to find that alternative that is most acceptable to the group, or to give feedback on different possibilities to reorganize the alternatives. The ease and flexibility of thus setting up and evaluating different forms of voting in principle allow strongly enhanced forms of democracy.
A quote from the announcement of "Computer Supported Cooperative Work (CSCW): An International Journal" provides more background information:
The journal arises as a timely response to the growing interest in the design, implementation and use of technical systems (including computing, information, and communications technologies) which support people working cooperatively. Equally, the journal is concerned with studies of the process of cooperative work itself - studies intended to motivate the design of new technical systems, and to develop both theory and praxis in the field. The journal will encourage contributions from a wide range of disciplines and perspectives within the social, computing and allied human and information sciences.In general, the journal will facilitate the discussion of all issues which arise in connection with the support requirements of cooperative work. It is intended that the journal will be of interest to a wide readership through its coverage of research related to - inter alia - groupware, socio-technical system design, theoretical models of cooperative work, computer mediated communication, human-computer interaction, group decision support systems (GDSS), coordination systems, distributed systems, situated action, studies of cooperative work and practical action, organisation theory and design, the sociology of technology, explorations of innovative design strategies, management and business science perspectives, artificial intelligence and distributed AI approaches to cooperation, library and information sciences, and all manner of technical innovations devoted to the support of cooperative work including electronic meeting rooms, teleconferencing facilities, electronic mail enhancements, real-time and asynchronous technologies, desk-top conferencing, shared editors, video and multi-media systems. In addition, we welcome studies of the social, cultural, moral, legal and political implications of CSCW systems.
[...] Detailed instructions for authors and other information (such as submission via email or on disk) can be obtained [...] by electronic mail on: HUSOC@KAP.NL (Please mark your message CSCW).
See also: information on CSCW and groupware on the Internet, CSCW Definitions and Abbreviations
Each node will typically represent a separate concept, and contain at least a definition and an exposition. The definition defines the concept in terms of other concepts, by providing specific semantic links to those concepts. (for an example, see our web of systems concepts). Primitive terms are undefined, or implicitly defined by their links with other primitive concepts. The exposition gives additional information about the concept (e.g. bibliographical or historical references, analogies, examples, applications), and may also contain different types of (referential) links. A node may contain text, formulas, drawings, ..., and even programs that perform specific operations (e.g. creating an instance of that concept, with specific attributes, or sending a "message" to another node).
Nodes will have a number of fixed fields, containing author, date (creation and modification), title, upward-references (referring the mother node) and downward references (referring to daughter concepts).
The meaning of a node is partially formal, determined by the network of semantic relations to which it belongs; and partially informal, determined by the personal interpretation of the user who reads the exposition, and tries to understand the concept by associating it with the context. Such a format allows the adequate representation of precise, mathematical concepts, of vague, ambiguous, "literary" ideas, and of the whole continuum in between.
See further: Joslyn C (1996).: Semantic Webs: A Cyberspatial Representational Form for Cybernetics, in: Cybernetics and Systems '96 R. Trappl (ed.), (Austrian Society for Cybernetics).
As with nodes, links come in a variety of types (though at present only one type is implemented). Examples of types of links include a variety of pragmatic categories, including: simple textual reference (e.g., looking up the definition of a word that is used in the definition of another); historical, bibliographical, and biographical reference; logical implication among concepts; and the historical development of a dialog among a group of authors.
Also included in link types are a variety of semantic categories, to
aid in the process of semantic analysis describe in section semantic,
including :
Heylighen has suggested a general scheme for the development of semantic relations in terms of fundamental logical and temporal distinctions.
See also: Joslyn C (1996).: Semantic Webs: A Cyberspatial Representational Form for Cybernetics, in: Cybernetics and Systems '96 R. Trappl (ed.), (Austrian Society for Cybernetics).
Such a goal has, however, proved elusive at best. Only a very few
researchers have explicitly pursued cross-disciplinary theories
\cite{OLR82,TRL88}. Rather than unification, recent systems theory has seen
a proliferation of new language and terminology. For example, the
Proceedings of the 1991 Conference of the International Society for
the Systems Sciences includes an excellent index \cite{ISSS91} of keywords
used in proceedings papers, listing keywords and the papers they were used
in. Table 1 shows a summary of the number of papers that
shared a certain number of keywords, and the keywords that were shared the
most.
| # Cross-References | # Papers | Keywords |
|---|---|---|
| 1 | 394 | |
| 2 | 48 | |
| 3 | 7 | |
| 4 | 3 | |
| 5 | 2 | Process Theory, Toroid |
| 6 | 1 | Living Systems Theory |
| 7 | 2 | System, Integration |
| 8 | 1 | Living Systems |
For example, the keyword "living systems" appeared in eight papers, and was the only keyword to do so, while both "system" and "integration" appeared in seven papers each. It should be noted that "Process Theory" and "Toroid" were each used by single author groups in multiple similar papers; that JG and JL Miller's "Living Systems Theory" \cite{MIJ78,MIJMIJ90} was a focus of a number of special sessions at the conference, which Profs. Miller and Miller attended; and that "System" is the single unifying concept of the entire society. The inclusion of the term "Integration" only reveals the irony of the absence of integration in the terminology used by members of the ISSS. This is demonstrated by the exponential distribution of keyword sharing.
We can conclude that there is virtually to terminological cohesion in the systems field.
Principia Cybernetica proceeds from the assumption of the early systemists, that a primary purpose of Cybernetics and Systems Science is to move towards the unification of science, in part (but only in part) through terminological unification and reduction. To that end, a primary purpose of Principia Cybernetica will be to perform semantic analysis on terms and concepts through the explication of their various senses in the context of their historical development. It is intended to identify synonyms, perhaps adopting a single term to replace anachronistic, specialized, or otherwise obsolete usages from the family of terms. Sometimes there will be good criteria to select the term, other times the term can be chosen arbitrarily without loss of generality. Otherwise, a variety of semantic relations can be identified, for example antonym, generalization or instance. New terminology will only be introduced as a last resort. In this way, we intend to be able to adopt a single coherent set of terminology to be used to develop Metasystem Transition Theory.
On Cybernetic Epistemology)
This is the method universally used in science. We first rely on an
intuitive understanding of simple concepts, then on the basis
of this understanding we convey the meaning of more formal and exact,
but also more complex, concepts and ideas.This statement itself is an illustration of our method. We used in it the words 'understanding', 'meaning', 'formal'. In due course, these notions should be analyzed and 'more formal and exact' meanings should be given to them, in their turn. These new meanings, however, will not come to replace the original meanings, but to make an addition to them.
Compare this with the situation in physics. We start this branch of science speaking about bodies and their masses, measuring distances in space by applying rulers, etc. Later, when we study the structure of matter, we find that those bodies and rulers, are nothing else but certain structures consisting of huge numbers of atoms. This concept of a ruler is, however, a new concept, even though it refers to the same thing. To come to the concept of a ruler as an atomic structure, we must pass a long path, at the beginning of which a ruler is a simple thing the usage of which is easy to explain.
In the Principia Cybernetica Project, we approach philosophy with the standards and methods of science. We try to define and explain such basic things as `meaning', `understanding', `knowledge', `truth', `object', `process' etc. But to explain, e.g., understanding, we must rely on understanding in its usual intuitive sense, because otherwise we will not know if we ourselves understand what we are saying; so, there will be little chance for our words to be meaningful.
Or take the concept of an object. We have a conceptual node devoted to it. But we cannot do without speaking about objects long before we come to that node -- in a close analogy with the two concepts of a ruler in physics.
Relations between things in this world are very often circular, so we are often at a loss when trying to start and finish definitions. Using various levels of formalization allows us to avoid vicious circles in definitions. Suppose we use informally some concept A to define a concept B. Let us represent the fact that A conceptually precedes B, or B relies on A as A < B. Then we want to make A more exact: A'. We define it, and discover that it now depends on the already defined B. Hence if we were to require that in a formal definition of a concept all the concepts on which it relies are formally defined, we would either have to limit ourselves to a strictly hierarchical subset of concepts (which will be far from universal), or never finish the job, moving in a vicious circle. Instead, we recognize that there are various levels of formalization of concepts which refer to the same parts of the world, concept, and we allow these concepts to coexist. Thus after defining B with the use of A, we define A' using the informal concept B; since B relies on A, the old, informal version of A is not discarded, but stays in the system of concepts. Now we could make the definition of B more formal, basing it on A' instead of A; on the next turn of this spiral, we may wish to define even more formal concept A'', etc.:
A < B < A' < B' < A'' < B'' ... etc.Whenever we want to understand a definition, we start unwinding the chain of dependent definitions from right to left, until we come to basic intuitive notions about which there should be no disagreements.
An advantage of the present definition is that it is more or less equivalent with the sense of "formal" as it is used in mathematics and the sciences. A scientific theory is called "formal" when it is expressed in a form (usually mathematical) such that there is no ambiguity as to the meaning and implications of its expressions. This implies that the same statement read by two different scientists, at different moments and in different parts of the world is supposed to be interpreted in exactly the same way. Even computers, which are totally unaware of context, should be able to interpret a fully formalized statement. Striving to "formalize" theories or hypotheses is an essential part of the quest for objectivity, universality and repeatability that characterizes scientific research (Heylighen 1992b).
It must be noted, though, that complete formal description is in principle impossible. Even in pure mathematics it is recognized (through the theorem of Gödel) that it is in general impossible to explicitly state all the necessary and sufficient conditions for a particular expression to be valid. There always remains an element of indeterminacy, and completely unambiguous description is impossible. This is confirmed in the physical sciences by Heisenberg's "Uncertainty Principle", which is related to the "Observer's Paradox" in the social sciences. On a more intuitive level, the principle can be explained by noting that the meaning of an expression can only be fixed by means of a definition, which explicitly states the background knowledge or information about the context needed to understand the expression. However, the definition itself contains new expressions which need to be defined themselves. But those second-order definitions again contain new terms which must be defined, ..., and so on, in an endless chase for a complete description of the world.
On the other hand, expressions must have a minimal formality in order to be understandable at all. If the meaning changed with the slightest variation of context between the utterance of the expression and its interpretation, communication would be impossible, as the sender and the receiver of the message will never share exactly the same context. For example, there will always be a certain lapse of time passing between the moment a sender forms an expression in his or her mind, and the moment the receiver has processed that expression. Sender and receiver will also always have a somewhat different background knowledge and awareness of the present circumstances. So, a minimal invariance of meaning over changes of context is necessary.
Similarly, complete fuzziness merely signifies that any interpretation is as likely as any other one, and that implies that the expression is totally devoid of meaning or information.
We must conclude that formality is a relational concept: an expression can be more or less formal relative to another expression, implying an ordering of expressions, but no expression can be absolutely formal or absolutely informal. All linguistic expressions will be situated somewhere in between these two extremes. Where exactly on that continuum the expression will lie, depends on the choices made by the one who produces the expression, which in turn depends on the situation and the personality of the sender.
Reference: Heylighen F. & Dewaele J-M.: "Formality
of Language I: definition and measurement", submitted to Applied
Linguistics
| Synopsys: |
Grouping words in the traditional grammatical categories (nouns, verbs, prepositions, etc.), this produces the following formula for formality (F):
F = (noun frequency + adjective freq. + preposition freq. + article freq. - pronoun freq. - verb freq. - adverb freq. - interjection freq. + 100)/2
Such a formula provides an easily applicable measure for ordering language from different sources, genres or styles according to their formality. The calculated formality corresponds generally quite well with intuitive expectations, e.g. official documents or scientific texts are more formal than personal letters, speeches are more formal than conversations, etc. For example, data for Dutch reveal the following ordering:
| context-independent categories | deictic categories | ||||||||||
| Nouns | Articles | Prepos. | Adject. | Pronouns | Verbs | Adverbs | Conjunc. | Formality | |||
| Oral Female | 10.40 | 6.89 | 5.86 | 8.09 | 16.95 | 19.35 | 17.45 | 7.47 | 38.7 | ||
| Oral N.Acad. | 12.75 | 8.50 | 6.34 | 6.71 | 16.01 | 18.80 | 19.31 | 6.34 | 40.1 | ||
| Oral Male | 11.48 | 8.16 | 6.69 | 7.63 | 15.84 | 18.45 | 16.53 | 7.05 | 41.6 | ||
| Oral Acad. | 13.16 | 9.58 | 7.91 | 7.13 | 13.96 | 17.75 | 17.88 | 7.13 | 44.1 | ||
| Novels | 18.52 | 10.48 | 10.26 | 10.00 | 13.25 | 20.62 | 10.47 | 6.06 | 52.5 | ||
| Fam. Magaz. | 21.78 | 9.77 | 12.21 | 11.14 | 10.09 | 18.71 | 9.74 | 6.39 | 58.2 | ||
| Magazines | 24.20 | 11.61 | 13.90 | 10.93 | 8.55 | 17.68 | 8.73 | 4.34 | 62.8 | ||
| Scientific | 23.10 | 15.00 | 13.75 | 10.75 | 6.71 | 16.58 | 7.98 | 5.98 | 65.7 | ||
| Newspapers | 25.97 | 14.68 | 14.54 | 10.57 | 5.62 | 16.69 | 7.21 | 4.70 | 68.1 | ||
The scientific process, like all evolutionary processes, is fundamentally progressive: information (if not knowledge) accumulates. Although classical, naive ideas about a monotonically growing body of knowledge asymptotically approaching an empirical "truth" are largely discredited (e.g.\cite{KUT62}), even the refutation of a scientific theory is the result of an increase in the total quantity of information. But if this growth in information is not balanced by a process which selects information for its value in some context (e.g. through the refutation and abandonment of theories), then science will ultimately become untenable and unviable. The limit of selection of knowledge is consensus, the reduction to one accepted theory or premise.
All traditional scientific subjects rest on a process of consensus-building by its practitioners, of the construction of a body of shared knowledge. (The necessity of social consensus for the construction of viable social structures is discussed in \cite{TUV82}.) Of course healthy and vibrant debate continues about many aspects of theory in all disciplines, and is further necessary to continue it. But of course it is exactly those active arguments which draw our attention to the leading edge of a scientific field. Underneath, successful disciplines rest on a large body of theory which is held consensually by virtually all practitioners. While the scientific method must admit of the possibility of the refutation of e.g. quantum electrodynamics, plate tectonics, or the gene theory the likelihood of such refutation is vanishingly small, and in practice and effect the inductive inference to accept them as "true" is admitted.
It is deeply regrettable that the history of Cybernetics and Systems Science has seen little movement towards such a consensus. First, there is a long schism between those who would regard "cybernetics" as primary and others who would regard "systems theory" or "systems science" as primary \cite{KLG70,?}. This view was not shared by the founders of the movement, but has resulted in an unconscionable dilution of the efforts and strengths of cyberneticians, perhaps even worse than the external forces that tend to be brought to bear against interdisciplinary study.
On the contrary, we hold that Cybernetics and Systems Science are at most two aspects of one field of study, dedicated to the concept of general systems as complex informational networks, rich in feedback and in constant interaction with each other and their environment. While the background and work of the Principia Cybernetica Editors and other participants spans many aspects of this field, and as noted above terminological convenience sometimes necessitates the contrary, it is generally the policy of Principia Cybernetica to refer to the dual fields of Cybernetics and Systems Science together, and thus to always stress their inherent unity.
Our purpose is to explore and explicate this theoretical fabric, in the expectation that it is such efforts which will yield a general and rigorous science of cybernetic systems viable and feasible. It is the ultimate goal of Principia Cybernetica to establish a theory which can be consensually held by all cyberneticians. However, we do not see this consensus as a narrow, normatively imposed, monolithic edifice. First, the consensus itself is always open to debate and revision. Indeed, the very process that we envision for the development of Principia Cybernetica is evolutionary and dynamic.
But also, we fully recognize that any achieved consensus will inevitably be shared by a limited research community, perhaps only the Editors. As we proceed, we must always remember that this effort is one project built by individuals who are necessarily rooted in their own experiences, abilities, and perspectives. Therefore, we regard our consensual construction as a cybernetic philosophy, not the cybernetic philosophy. To distinguish our philosophy from others, we call it "Metasystem Transition Theory" (MSTT), based as it is on the principle of the Metasystem Transition.
However, Principia Cybernetica is also a collaborative work, and will thus necessarily involve people other than the Editors and others who both agree and disagree with them. Furthermore, it is inevitable that differences will flourish among the Editors, although hopefully about rather minor matters. To facilitate these realities, portions (nodes) of Principia Cybernetica are divided into three categories:
Many different people have already contributed in one of these ways to the Project's development. You too can join our efforts and become a contributor (see Collaborators Needed). If you would like to help, you may check the list of tasks where we would appreciate support. If you have already contributed something to the Web or to PCP at large, you are invited to add your name and personal coordinates or comments to the Web, by annotating the List of Contributors.
If you just want to make a quick comment about an existing document, you would better write an annotation to that document. Annotations are not reviewed: everything entered there is immediately published (really stupid or irrelevant comments may still be deleted afterwards). However, annotations do not have the same status as normal PCP nodes: they are not included in the "Table of Contents" or "Recent Changes", (though they can be found through the searchable index). They belong to the category of "discussion nodes", rather than the default "consensus nodes" or "individual contribution nodes" (see Consensus Building). If you check the list of user annotations you will see that few annotations are really detailed, well-formulated and well-thought out texts. They are mostly one-line comments, links, tests or questions, and are not of the same level of quality as other nodes.
In order to qualify as individual contribution nodes, texts submitted to the board must be in the general PCP spirit, and discuss topics related to those that are already there. For inspiration, look at the nodes that are still empty: perhaps you might like to write a discussion of that topic? They should ideally also fit into the PCP hierarchy (i.e. have a specific "Parent node" of which they are the "Child"; if no appropriate parent exists, you can suggest one, under an existing parent, etc.). They should also have the typical format of PCP nodes: discuss a single idea in some detail but not too long, and provide many cross-references to other concepts used in the discussion. The style should be objective or scientific, yet easy to read. Look at existing PCP nodes for examples.
PCP web is not a medium for publishing journal-like papers. It is more like a continuously expanding and improving encyclopedia of fundamental ideas. We prefer short, in depth articles in a dictionary-like or encyclopedia-like style, treating basic ideas on the intersection of cybernetics, systems, evolution and philosophy. If you want to write longer discussions, you should better split them up in one parent node and several children (or grand-children). The better and more in line with the general PCP aims the node is, the more prominent a place it may get in our Web. The average PCP node is at present read some 800 times per year, which is more than most papers in scientific journals, so it is worth the effort to clearly formulate and publish your ideas in this way.
New nodes can be based on existing texts that have a nodelike structure (see the Web Dictionary and the Memetic Lexicon as examples). However, these texts should obviously be either unpublished or have copyright waivers (for example for "out of print" books, such as "The Macroscope", the copyright usually returns back to the author). On the other hand, we don't mind material that is adapted from or similar to already published material (e.g. papers), as long at it is not literally the same.
Texts can be submitted in ASCII, HTML or RTF (MS Word), preferably with minimal formatting. If not submitted in HTML, please indicate which words should be linked to other nodes in or outside of PCP Web. For texts longer than a few lines, please divide in paragraphs and if necessary in subsections with adequate headings. Please avoid fancy layout or color schemes: clear and simple is preferred. Figures and other illustrations are welcome as long as they are directly relevant, and not too large in byte size.
If you don't plan to get involved in email discussions, but stil would like to help, we would appreciate if you would send a note to one of the editors (Joslyn for PRNCYB-L subcriptions, Heylighen for other information) containing the following information:
1)Name
2)Email address
3)Postal address
4)Phone
5)Affiliations
6)How did you hear about PCP?
7)Please take at least one page to describe your work and how it might relate to PCP (this may be skipped by people who have contributed to PCP before).
8) What do you concretely suggest as a way in which you could support the project?
We would appreciate existing material which can enhance the Web, e.g. glossaries, dictionaries or definitions of cybernetics-related terms, icons or illustrations to embellish the Web, links to related servers, ... We are in particular looking for people with experience in hypermedia and computer-supported collaborative work environments, who might help us in choosing or developing the right software tools, and in general extend the functionality of the Web. We would also appreciate help with the administration: sending out mail, editing and printing newsletters and documents, connecting different communication channels (e.g. translating printed or faxed text to electronic texts). If you would dispose of secretarial or technical facilities, or have the time to help, please contact us.
If you feel a strong resonance with Principia Cybernetica and the views we are expressing, we would also be very interested in talking about involvement at deeper levels.
If you have any further questions or proposals about contributions to PCP, please contact one of the editors.
PRNCYB-members. The following is meant to become an exhaustive list of "Home Pages" with the names, addresses and other information about all people having contributed to the project. New contributors are invited to add their own homepage to this list, by annotating this node. If you already have a home page on a different server, you can simply include its address and leave the text of your annotation empty. Otherwise, you can type in your coordinates and other useful info in the annotation text field.
|
Lic. Experimental Psychology |
| Assistant Researcher FWO (Fund for Scientific Research- Flanders) | |
| Project leader Dr. Francis Heylighen. | |
| Address: | |
| Vrije Universiteit Brussel, Center Leo Apostel | |
| Pleinlaan 2, 1050 Brussels, Belgium. | |
| Tel. : + 32 2 644 26 77. & E- Mail: jbollen@vub.ac.be |
| Research interests: |
Learning hypertext networks, associative and distributed knowledge representation, dynamical and evolutionary approaches to knowledge development
| Present research: |
I'm currently investigating learning rules that use the paths users follow through a hypertext to re-organise the network, so that it restructures itself into a representation of the users shared semantic structure.
The assumption that led to the development of hypertext/media interfaces is that hypertext networks, because they use associative and distributed representations of knowledge, are in some way more compatible with how humans store and retrieve information. Networks that more accurately represent their users' semantical structure will thus allow users to retrieve information more effectively.
As most hypertext networks, such as the WWW, are at present developped and designed by human web masters, that have only very limited knowledge and insight into what a good hyper structure should be, it can be expected that information retrieval and storage is at present highly inefficient. Our research suggests a number of locally learning rules that can automatically, without human intervention, make hypertext networks re-organise and streamline their structure
This link points to a short paper titled Adaptive Hypertext Networks That Learn The Common Semantics Of Their Users., which will be published in the proceedings of the International Congres on Cybernetics in Namur, August 21-25, 1995. You are invited to read this article and mail reactions, criticism or suggestions via the above provided E-mail link.
Photo: giving a seminar on learning webs at Goddard Space Flight Center, NASA.
I was born on November 5, 1971 in a small town famous for its historical sites and periodical floodings as the first son of three. My parents loved me because I was pink, cute and learned fast. Soon I discovered speech and thought and so did everybody else. I developed into an extremely curious and loud child with a preference for electrical appliances.
My main interests at school were the mathematics and electronics classes but after 4 years of Industrial Sciences (at highschool level as a preparation to Engineering at university level) I decided to turn to a more fundamental science. Psychology seemed to be a perfect choice.
I graduated with a thesis on a self-organising system for an autonomous agent. The system was based on a neuro-chemical model of conditioning effects developed by Hawkins and Kandel which was linked to a set of drives like hunger and "mating-need". The agent learned to make temporal associations between the selection of a certain activity and it's drive reducing effects. I will gladly mail a copy of my thesis if your interested in the subject.
As for my hobbies: I love medieval and Barocque music written by DeNassus, Monteverdi (essentially all Flemish polyphonic music) and Bach (his works on the organ), allthough the older material from the Sonic Youth, George Clinton and Herby Hancock can make me dance. I read books too! (some without pictures!) I love the classic SF stuff about space-robots and alien threats. My favourite authors are Heinlein, Asimov, VanVogt and the guy who wrote Ringworld.
So here it is. Let me know if you have any suggestions for listening or reading. Da shledanou.
Lehigh University.Campbell was one of the truly important thinkers in evolutionary philosophy and social science methodology, and one of the most cited authors in the social sciences. He was a past president of the American Psychological Association, a distinction comparable to a Nobel prize in psychology. As a recent newsgroup message called him: "A very great experimental psychologist and methodologist (perhaps the greatest)" (Claire Gilbert, blazing@crl.com).
We had made him a honorary "Associate" of the Principia Cybernetica Project (see the project's Masthead), since he had always supported our plans to collaboratively develop an evolutionary-cybernetic philosophy. I recently had the chance to collaborate with him on a paper entitled "Selection at the Social Level" (published in a special issue of "World Futures"), and we had plans to write further joint papers on the evolution of social systems. Alas, that cannot happen anymore.
The announcement included below emphasizes Campbell's contribution to experimental methodology. So let me remind you of his more philosophical contributions. He was the founder of the domain of "evolutionary epistemology" (a label he created), in which he generalized Popper's falsificationist philosophy of science to knowledge processes at all biological, psychological and social levels.
Within that domain his main contributions are the concepts of: 1) "Blind Variation and Selective Retention (BVSR)", where he emphasizes the fact that knowledge initially can only be developed by trial-and-error, and 2) "vicarious selectors", which allowed him to explain how initially blind trials could develop into intelligent search guided by knowledge developed earlier. He generalized the hierarchical organization of vicarious selectors in his analysis of the phenomenon of "downward causation" (another term popularized by him), where a higher level system or whole constrains its parts.
He applied this same evolutionary philosophy to the development of social systems, arguing that cultural evolution is necessary to explain the development of human society. The necessary tension between cultural and biological evolution allowed him to explain the organization of archaic societies and the emergence of religious systems. He used these insights to plead for the development of an evolutionary ethics, which could guide our actions without recurring to arbitrary metaphysical principles. He also applied these ideas to some problems in present-day society, arguing for alternative types of social organization, without falling into the trap of designing utopias which only work on paper.
The depth and thoroughness of his thinking, his attention to detail, and the width of the interdisciplinary terrain he covered (from psychology to anthropology, sociology, education, biology, philosophy and systems theory), should be an example to us all. Although he is no longer here to teach us in person, he leaves behind a wealth of writings which will inspire researchers for the decades to come. A small sample of his work can be found in his and Gary Cziko's of evolutionary epistemology.
The obituary below gives some more details about Campbells work in methodology.
> From: Burt Perrin <100276.3165@COMPUSERVE.COM> >[...] > > Don Campbell was one of the giants-arguably *the* giant-in evaluation as > well as in social psychology, philosophy of science, and in many other fields. > He was one of the few true rennaissance men of our day, although I am sure he > would reject the label. He spoke with people across many different disciplines > and many different theoretical orientations, acknowledging the contributions > of all. > > He set the intellectual direction for evaluation. For example, he reminded us > that that our goal, as researchers and evaluators, is to aim to eliminate rival > competing hypotheses through the simplest means possible. Campbell may be best > known within evaluation circle for coining the concept of quasi-experimental > designs and for advocating use of experimental methods for evaluation. Perhaps > less well known is that Campbell did not hold these methods to be a priori > superior to any other. Long before it became fashionable to do so, he also > strongly defended the use of qualitative methods-and indeed of the application > of common sense. The method must follow the question. Campbell, many decades > ago, promoted the concept of triangulation - that every method has its > limitations, and multiple methods are usually needed. > > I had the privilege of studying with Campbell in the 60s at Northwestern > University - before anyone spoke of evaluation. He was my major intellectual > inspiration. I remember how he frequently welcomed me-a lowly undergraduate- > into his office - and invariably could insert a hand into a file cabinet or a > pile of papers on or near his desk - and pull out something he had written > about almost any conceivable topic. > > I will stop now. Program evaluation, psychology, philosophy, and humankind has > suffered a major loss. > > Burt Perrin > Toronto, Canada > 100276.3165@compuserve.com
See also: Donald T. Campbell, Master of Many Disciplines,
Dies at 79
obituary in the New York Times
Dr. Jean-Marc Dewaele is a
Lecturer in Interlanguage studies; French linguistics and
sociolinguistics at the Department of
College. He received a
Ph. D in romance languages and literature, at the
Vrije Universiteit Brussel with "summa cum laude", in 1993, with a dissertation entitled
'Variation synchronique dans l'interlangue française'This work is situated in the field of Applied Linguistics and builds on the model developed by Levelt, 1989. Interstylistic and interindividual variation was analysed in the French interlanguage of 39 Dutch-speaking students. Variation was measured through a number of quantified linguistic variables indicating the level of formality, fluidity and complexity of speech. Factor analysis and multivariate analysis was used to identify the situational, social, psychological and sociobiographical variables that underlie the observed variation.
To appear :
Prof. Dr. Francis Heylighen is a Research Associate ("Onderzoeksleider") for the Fund for Scientific Research - Flanders (FWO). He works at the Free University of Brussels (VUB), where he is an Associate Director of the transdisciplinary research Center "Leo Apostel" (CLEA). He is editor of the world-wide Principia Cybernetica Project for the collaborative development of an evolutionary-systemic philosophy.
The main focus of his research is the evolution of complexity, which he approaches through the theory of metasystem transitions. He has worked in particular on the evolution of knowledge (see his 1994 project ), and its application to the emerging intelligent network (the "global brain"). He uses these ideas as a framework for the integration of knowledge from different disciplines into a new "world view". He is presently writing a popular science book presenting this evolutionary world view to a broad audience, and is looking for agents or publishers interested in this project.
In addition, he has done research and published papers about different topics in diverse disciplines:
Joslyn and Valentin Turchin)
You can find references to his work on other web pages, such as a satirical interview in "Wired", an interview with the futurologist Joël de Rosnay (in French), or the list of "Great Thinkers and Visionaries on the Net".
| Synopsys: |
This transdisciplinary work proposes a cross-fertilization between cognitive science and theoretical physics, within a framework inspired by systems theory. Cognitive science concepts are applied in an epistemological analysis of physical theories, considered as representations of change.
This analysis leads to the basic concept of distinction conservation, which appears necessary and sufficient to demarcate classical representations (classical mechanics) from non-classical ones (quantum mechanics, relativity theory and thermodynamics). It is observed that the most important cognitive and physical processes are non-classical (i.e. do not conserve distinctions), whereas the paradigms used for modelling and interpreting them are basically classical. This anomaly produces conceptual problems, exemplified by the paradoxes of quantum mechanics. The construction of an adaptive metarepresentation is proposed in order to solve these problems. This is a general framework for the representation of not distinction-conserving processes and representation changes. Finally a first sketch of a metarepresentational formalism is presented.
The book is addressed to a broad audience of researchers from different backgrounds. It is written in a style which avoids technicality, explaining difficult mathematical and physical concepts in the most simple way. It will be especially stimulating for philosophers and systems theorists interested in the integration of theories, for cognitive scientists involved in the application of ideas from physics, and for physicists wishing to understand the epistemological foundations of their models.
The addendum was written in February 1987. It contains a reformulation of the main results of the work in a more formal manner, and shows how basic structural properties of different physical theories can be deduced from a few general axioms. I have also included an additional list of references (after the original bibliography), containing papers which were written after the first version of the work, and which contain some elaborations of ideas in the work, especially in relation to autonomous systems and to the dynamics of distinctions.
The primary purpose of this framework would be to integrate existing concepts, theories and disciplines and thus to eliminate paradoxes and confusions. Its secondary purpose would be to allow new applications in the analysis and steering of processes in which new representations (i.e. new knowledge) are generated.
This framework would be the first stage in the development of a general theory of representation and representation dynamics. Such theory is called an "adaptive metarepresentation".
The representation problem formulated in this context leads to two more concrete research questions. In physics the main problem can be phrased as follows : "How to integrate classical and non-classical representations of the same dynamical systems ?" This difficulty can be illustrated by the well-known paradoxes of quantum mechanics. In cognitive science the basic question is : "What are the fundamental structures of representations and how do they evolve ?"
These problems are approached through an analysis consisting ofthe following subsequent steps :
2) the analysis of classical scientific theories (in particular classical mechanics) with the help of these concepts leads to a hierarchically structured, coherent and self-sufficient representation structure : the classical frame. Its subsequent levels are : objects, predicates, Boolean algebra, state space, topology, time as a continuous parameter, operator group, dynamical constraints. It is shown how these different substructures are interdependent, and how their use determines the world view of the subject who uses this frame. In particular it is shown by different examples how the unconscious bias of the classical frame leads to the rejection or to the ignorance of those phenomena which do not fit into its formal structure.
3) yet the classical frame appears very natural and stable so that we cannot dismiss it as just one of a multitude of possible representation structures. Therefore we should find the feature which makes classical representations unique and which distinguishes them from all other non-classical representations. This criterion is found by going back to the most fundamental mechanism of cognition : distinction. It is shown that the classical frame is characterized by the absolute invariance of all distinctions which determine the representation structure : the distinction between a proposition and its negation, the distinction between space (simultaneity) and time (precedence). Hence distinction conservation appears to be a necessary property for a representation to be classical. We should now also show that it is sufficient, i.e. that non-classical representations do not possess this property.
4)a) Quantum mechanics : it is shown that during the quantum observation process, which is described by "the collapse of the wave function", there is no conservation of certain distinctions describing the system. This expressed in the quantum formalism by the superposition principle and the projection postulate. It is shown how this structural feature of the quantum representation can be reduced to the existence of a non-trivial orthogonality relation between quantum states. This leads to a non-Boolean logic and to a non-Bayesian probability expression.
The cause of this non-conservation is analysed and found to be due to the impossibility of perfect self-determination for a macroscopical observation apparatus. This leads to the impossibility of perfectly distinguishing microstates. The non-disjointness of the resulting macrostates explains the non-Bayesian probability and hence the fundamental structure of the Hilbert space formalism.
b) Relativity theory : the relativity principle and the existence of a finite maximum speed for signal propagation entail the relativity of simultaneity and synchronization. Hence the distinction between simultaneous and non-simultaneous events loses its invariance. Instead we find a causal structure determined by an incomplete precedence relation.
It is shown that this space-time structure can be reconstructed by classifying the paths formed by locally distinction conservation connections between events. The cyclic paths are shown to be unable to transfer information : either they lead to static correlations, or to so-called "causal paradoxes" which can be eliminated by deleting the self-inconsistent distinction. The remaining global connections determine three relations which are proven to be sufficient to define a "causal structure" (in the sense of Kronheimer and Penrose). We may conclude that the non-classical space-time structure of relativity theory is the direct consequence of the principle of the impossibility of circular information transfer.
c) Theories of irreversible processes : complex systems are characterized by so-called irreversible processes in which the total internal information of a system can only diminish (2nd law of thermodynamics). In open systems this can be compensated by an external input of information. It is shown that this non-conservation of distinctions is due to the interdependence of macroscopical and microscopical distinctions : for a macroscopical observer it appears as though macroscopical distinctions simply dissappear (diffusion, entropy increase) or appear out of nothing (self-organization, bifurcation).
This non-classical irreversible evolution is a necessary prerequisite for the appearance of autonomous, adaptive, and cognitive systems which are able to create and to maintain their own boundary (i.e. their self-environment distinction) by internally processing the incoming information. Here also we may suppose that this irreversible information process is due to the principle of incomplete self-determination.
5) since we have shown in 4)b) that the topology of space-time and hence locality is dependent upon the non-circular transfer of distinctions (hence information) there is no longer any paradox in the fact that there are non-local influences during quantum observation experiments, since no information is transferred. The non-local correlations can be explained by the (non-local) creation of a distinction by the observation apparatus. Hence no local "hidden variables" are to be introduced.
6) The static scheme of distinctions which was found to form the base of classical representations can be formalized by means of the distinction algebra of Spencer-Brown, which can be realized as a Boolean algebra B. Classical (i.e. distinction-conserving) processes can then be represented by a group of automorphisms of the algebra. Non-classical processes can be represented by general morphisms sending the algebra B upon different algebras. These processes can also be interpreted as transformations sending the classical representation B upon a new classical representation B'. Hence this framework can be seen as a basis for an adaptive metarepresentation in which all classical and non-classical representations and their transformations can be expressed.
1. Prologue : The Conceptualization of Change
2. The Representation Concept in Physical Science and in Cognitive Science
2.1 Physical Science
2.2 From Physical Science to Cognitive Science
2.3 The Philosophical Theory of Ideas as Representations of
External Objects
2.4 Artificial Intelligence and Knowledge Representation
2.5 AI and Problem Representation
3. Adaptive Representations.
3.1 Representations as an Interface between Mind and Nature.
3.2 Adaptation as Vicarious Selection
3.3 The Thermostat as an Example of an Adaptive Representation
3.4 The Interdependence of Feedback and Feedforward.
3.5 Structures and States of an Adaptive Representation.
3.6 Information-Processing in an Adaptive Representation
4. Making Representations Explicit.
4.1 Scientific Theories as Explicit Representations.
4.2 Formalization and Paradigmatic Structures.
4.3 Operationalization and Empirical Tests.
4.4 The Problem of Transdisciplinarity.
4.5 The Need for a Metarepresentation
5. The Structure of the Classical Frame
5.1 Introduction
5.2 The Generation of Elementary Expressions
5.3 The Function of Objects and Predicates.
5.4 The Generation of Compound Expressions.
5.5 From Boolean Algebra to State Space
5.6 Topology, Time and Trajectories in State Space
5.7 The Group of Dynamical Operators.
5.8 Dynamical Constraints
6. The World View of the Classical Frame.
6.1 Introduction
6.2 The Ontology of the Classical Frame
6.3 The Epistemology of the Classical Frame
7. Classical and Non-Classical Representations.
7.1 Beyond the Classical Frame.
7.2 Distinctions as Basic Elements of a Representation
7.3 The Invariance of Distinctions in the Classical Frame.
8. Quantum Mechanics
8.1 The Complementarity of Representations.
8.2 The Structure of the Quantum Formalism.
8.3 A Cognitive-Systemic Interpretation of Quantum Mechanics
8.4 From Classical to Quantum Probability
8.5 Information Transfer during the Observation Process.
9. Space-Time Theories and Causality.
9.1 The Relativity of Reference Frames.
9.2 The Relativity of Simultaneity and Synchronization
9.3 The Invariance of the Causal Structure of Space-Time
9.4 From Local to Global Causal Connections
9.5 Formal Properties of Global Causal Connections
9.6 Non-Locality Paradoxes in Quantum Mechanics.
9.6.1 The Paradox of de Broglie
9.6.2 The EPR Paradox
9.6.3 The Aharonov-Bohm Effect.
10. Irreversible Information Processes : from Statistical Mechanics to Cognitive Psychology
10.1 Introduction
10.2 Irreversibility in Statistical Mechanics
10.3 Self-Organization.
10.4 Autonomy and Adaptation
10.5 Perception and Problem-Solving as Irreversible Processes
10.6 Learning and Discovery as Representation Changes
11. Summary and Discussion of the Previous Results
11.1 Different Formulations of the Research Problem.
11.2 Lessons Learned by Analyzing Classical Representations.
11.3 The Correspondence between Classical Metarepresentations
and Non-Classical Object Representations.
11.4 Lessons Learned by Analyzing Non - Classical Representations
12.1 Introduction.
12.2 Distinction Algebras
12.3 Kinematical Constraints for Distinctions.
12.4 Categories of Distinction Algebras
12.5 The Relation between Categorical and Boolean Algebras
12.6 The Dynamics of Distinctions
12.7 Towards an Operationalization of the Theory
Introduction
Basic Concepts and Assumptions oftheMetarepresentational Framework
The Classical Representation Frame.
The Quantum Mechanical Frame
The Relativistic Frame
The Thermodynamical Frame
Conclusion
Communication & Cognition
Blandijnberg 2,
B-9000 Gent,
Belgium
Expiry Date:............................
Signature: ............................
And I will receive the book at the following address:
Name:
Address:
Country:
Please send this form by postal mail or fax to:
Communication & Cognition
Blandijnberg 2,
B-9000 Gent,
Belgium
Francis Heylighen was born in 1960 in Vilvoorde, near Brussels, in Belgium. He received his university degree in mathematical physics in 1982, and his Ph.D. in 1987, from the Free University of Brussels (VUB).
He is presently a Research Associate for the Fund for Scientific Research - Flanders (FWO).
He has been working as a researcher at the VUB since 1982, first concentrating on the foundations of physics (quantum mechanics and relativity theory), then on the cognitive and systems sciences. His work resulted in the construction of a transdisciplinary framework for the analysis and development of concepts and models, called "adaptive metarepresentation". It also forms the basis for an integrated evolutionary-systemic philosophy. This framework is based on a "dynamics of distinctions", which models how new structures emerge through recombination and selective retention of "closed" systems. It is being implemented as a computer support system for the structuring of complex knowledge domains, with applications for the self-organization of the World-Wide Web. Some of its implications have been empirically tested, in the domains of psychology and linguistics.
Heylighen has published over 60 papers, mainly in cybernetics and systems theory, a book (his PhD thesis, "Representation and Change"), and he has edited books on "-Steering and Cognition in Complex Systems", "The Quantum of Evolution" and "The Evolution of Complexity". He is editor and publisher of the "Principia Cybernetica Project", which attempts to consensually develop a cybernetic philosophical system, with the help of computer technologies for the communication and integration of knowledge. He is also Associate Director of the transdisciplinary research Center "Leo Apostel" at the Free University of Brussels.
He performs or has performed various scientific functions, including developer and publisher of Principia Cybernetica Web, administrator of the PCP-News electronic mailing list, chairman of the Global Brain Group, founder and secretary of the "Transdisciplinary Research Group" at the VUB, and co-founder of VUBO (the researchers association of the Free University of Brussels). He is a member of the editorial boards of the Journal of Memetics, the "Encyclopaedia of Life Support Systems", and the journal "Informatica" and has been a referee for the "International Journal of Man-Machine Studies". He has organized and chaired many international conferences, symposia and seminars, and is regularly invited to lecture in different countries.
All the World is Biscuit Shaped. . .
Valentin Turchin
Professor of Computer Science
Member of the Principia Cybernetica Editorial Board
Computer Science Department, City College, University of New York,
See also: local homepage
Prof. Valentin Turchin is originally from the Soviet Union. He
holds three degrees in theoretical physics, in 1952, 1957, and
1963, and worked in neutron and solid state physics.In the 1960's he turned his attention to mathematics and computer science, accepting a position at the Moscow Institute of Applied Mathematics. There he worked in statistical regularization methods and authored REFAL, one the the first AI languages. REFAL is a purely functional, pattern matching language with simple semantics, in the same class as LISP and PROLOG. It is currently the AI language of choice in the Soviet Union.
In the 1960's Dr. Turchin became politically active. In 1968 he
authored " Inertia of Fear and the Scientific Worldview", a
scathing critique of totalitarianism and an emerging cybernetic
social theory. Following its publication in the underground
press, he lost his research laboratory.
In 1970 he authored "The Phenomenon of Science", a grand cybernetic meta-theory of universal evolution, which broadened and deepened the earlier book. In 1977 it was published in English by Columbia University Press, followed by "The Inertia of Fear" in 1981.
By 1973 Dr. Turchin had founded the Moscow chapter of Amnesty International and was working closely with Andrei Sakharov. In 1974 he lost his position at the Institute, and was persecuted by the KGB. Facing almost certain imprisonment, he and his family were expelled from the Soviet Union in 1977. He came to New York and joined the Computer Science faculty of the City University of New York in 1979, where he currently teaches and owns the company Refal Systems Inc.
It is difficult to completely describe the scope of Dr. Turchin's work. Philosphical unity is achieved through the concept of the Meta-System Transition, in which higher levels of hierarchical control emerge in system structure and function. Dr. Turchin uses this concept to provide a global theory of evolution and a coherent social systems theory, to develop a complete cybernetic philosophical and ethical system, and to build constructivist foundation of mathematics. Using the REFAL language he has implemented a Supercompiler, a unified method for program transformation and optimization using the meta-system transition concept.
Joslyn, Cliff, and Turchin, Valentin: (1990) "Introduction to the
Principia Cybernetic Project", to be published, available by
electronic mail
Turchin, Valentin: /Cybernetic Foundation of Mathematics/, to be
published
/Computation and Metacomputation in Refal/, available with
software system
(1977) /Phenomenon of Science/, Columbia U., New York
Cybernetic theory of universal evolution. Metascience as a
cybernetic enterprise.
(1981) /Inertia of Fear and Scientific Worldview/, Columbia U. Press,
New York
Interpretation of totalitarianism from the persepctive of cybernetic
social theory.
(1982) "Institutionalization of Values", /Worldview/, v. 11/82
Review of Turchin's social theory and defense of reviews of
_Phenomenon of Science_ and _Inertia of Fear_.
(1985) "Orlov in Exile", /Physics Today/, v. 7/8
(1986) "Concept of a Supercompiler", /ACM Trans. of Prog. Lang. and
Sys./, v. 8:3
(1987) "Constructive Interpretation of Full Set Theory", /J. of
Symbolic Logic/, v. 52:1
Almost complete reconstruction of ZF set theory from a constructivist
philosophy, including implementation in the REFAL language.
Turchin, Valentin, and Joslyn, Cliff: (1989) "Cybernetic Manifesto",
[Local version of this home page (more up-to-date)]
Prof. Stuart A. Umpleby
Washington University,
Washington DC 20052, USA
He received degrees in engineering, political science, and communications from the University of Illinois in Urbana-Champaign. While at the University of Illinois he worked in the Biological Computer Laboratory and the Computer-based Education Research Laboratory (the PLATO system).
He has been using and designing computer conferencing systems since 1970. Between 1977 and 1980 he was the moderator of a computer conference on general systems theory which was supported by the National Science Foundation. This project was one of nine "experimental trials of electronic information exchange for small research communities." About sixty scientists in the United States, Canada, and Europe interacted for a period of two and a half years using the Electronic Information Exchange System (EIES) located at New Jersey Institute of Technology.
Umpleby teaches a course in system dynamics modeling. He constructed a system dynamics model of national development for the US Agency for International Development, and he was an instructor for several years in the AID Development Studies Program.
Since 1981 he has been arranging scientific meetings
involving American and Russian scientists in the area of
cybernetics and systems theory. In 1984 he spent part of a
sabbatical year at the International Institute for Applied
Systems Analysis, an East-West research institute located near
Vienna, Austria. In the spring of 1990 he was a guest professor
at the University of Vienna, of Medical Cybernetics and
Artificial Intelligence.
He is a past president of the American Society for Cybernetics.
The Cybernetics of Conceptual Systems
The Science of Cybernetics and the Cybernetics of Science
Strategies for Winning Acceptance of Second Order Cybernetics
Free University of Brussels, which automatically distributes announcements to all subscribers. This list is low-volume. In addition to a 2-monthly "newsletter" (see the PCP-news digest), it only carries
messages with information for all people interested in PCP, e.g.
conference announcements, Calls for Papers, new publications, new services, etc. This makes it easier for subscribers who don't like to get a lot of email, but still want to be kept informed about important events connected to the Principia Cybernetica Project. The list is moderated: only messages explicitly
approved by the listowner (Francis Heylighen) are broadcasted. Replies by default go to the individual who sent the message, and not to the list.
If you prefer a more frequent and interactive mailing list, you may apply to join our non-moderated list PRNCYB-L (membership conditions are minimal). All messages to PCP-news are simultaneously transmitted to PRNCYB-L (but not the other way around), so in any case you need only one subscription. PCP-news carries maximally 2 or 3 messages a month, while, like most discussion lists, the activity on PRNCYB-L fluctuates strongly, from about 10 to about 100 messages a month.
Unlike PRNCYB-L, you can automatically subscribe yourself to PCP-news. You will then get an introductory message about the mailing list, and start receiving all broadcasts on the list. You can unsubscribe in the same simple way.
At present, some 100 people, representing the five continents, subscribe to PRNCYB-L. The mailing list is of moderate volume (a few messages per week on average), but like all discussion lists this can fluctuate very strongly. Messages can be long and informative. Some topics that have been discussed include: entropy increase and self-organization, causality as covariation, thermodynamics and evolution of mortality, memetics and the evolution of cooperation, formal expression, criteria for reality, values and religion, definitions of "control", complexity and the edge of chaos, Robert Rosen's theory of anticipatory systems, etc. A selection of relevant information (e.g. congress announcements, publications; on hypertext, electronic publishing, evolution of the brain, ...) from other electronic forums is regularly cross-posted on PRNCYB-L.
Bruce Edmonds
maintains an HTML archive of
PRNCYB-L messages, sorted according to topic, date and
author, going back to the beginning of 1995. This includes a searchable index.
PRNCYB-L is not meant for casual discussion or uninformative technicalities. Nor is it meant as a general forum for discussion about cybernetics and systems science: other mailing lists, e.g. CYBCOM, already exist elsewhere. Whereas these lists are open to anyone with an interest in cybernetics and systems, PRNCYB-L is restricted to active participants and those who wish to be informed about the specifics of PCP.
For more detailed procedures on how to operate the PRNCYB-L server, check the common LISTSERV commands (note that most of these commands can only be used by people who have been manually subscribed to the list).
If you wish to join PRNCYB-L, please send in the subscription form. You will then be added to the mailing list, and receive initial instructions on how to operate the LISTSERV software (as subscription is done manually, this may take several days).
This form can also be used to change your subscription address. Simply unsubscribe your old address, then resubscribe the new or corrected one. Don't forget to do this if your email adress changes! Otherwise, the server will continue to send messages to your old address, generating errors, while you will stop receiving anything.
subscribe PCP-news endin the body of the message (subject can be empty) to the address majordomo@listserv.vub.ac.be. If you prefer to receive the messages from PCP-news at a different email address than the one you would be sending these lines from, just add your preferred address after the first line, e.g. "subscribe PCP-news jdoe@xyz.edu".
To unsubscribe you can similarly send the lines:
unsubscribe PCP-news end
Date: Wed, 6 Nov 1996 12:32:19 +0100 To: PCP-news@listserv.vub.ac.be Subject: Principia Cybernetica News - September/October 1996 Sender: owner-PCP-news@listserv.vub.ac.be Precedence: bulk GENERAL NEWS A first part of the new results, reached during the PCP board meeting in June, on the definition of control have now been incorporated into PCP Web (http://cleamc11.vub.ac.be/control.html). Moreover, our programs for self-organizing hypertext and retrieval of words through spreading activation can now be permanently consulted on the web, via a new node devoted to our research on learning, "brain-like" webs (http://cleamc11.vub.ac.be/learnweb.html). The PCP editor Cliff Joslyn has moved from Goddard Space Center, NASA, to the Los Alamos National Laboratory. His new address is: Mail Stop B265 Los Alamos National Laboratory Los Alamos, NM 87545 USA joslyn@lanl.gov http://gwis2.circ.gwu.edu/~joslyn The groups associated with PCP have also been quite active. The people involved with the electronic "Journal of Memetics" have reached consensus on an introductory text describing the aims of the journal, a general editorial policy, a managing editor (Hans-Cees Speel, hanss@sepa.tudelft.nl), and the constitution of an advisory board (presently Daniel Dennett, Aaron Lynch, David Hull and Gary Cziko). At the moment, they are looking for authors wishing to contribute to the first issue, which is scheduled for 1997. If you are interested to write a paper or take part in the reviewing process, please contact Hans-Cees Speel. The "Global Brain" group (see http://cleamc11.vub.ac.be/gbrain-l.html) has started its discussions on superorganisms and networks playing the role of nervous systems. Thanks again to Bruce Edmonds (who already created the PRNCYB-L archive, and the Journal of Memetics list and web site), an archive of the discussions can now be consulted at http://www.fmb.mmu.ac.uk:80/~majordom/gbrain/ WHAT'S NEW IN PCP WEB The following nodes in Principia Cybernetica Web have undergone substantive editing, or have been newly added during the months of September and October, 1996. (all documents are available via http://cleamc11.vub.ac.be/recent.html) * Oct 31, 1996: Basic References on the Global Brain / Superorganism (Gaines paper added) * Oct 30, 1996: References to Principia Cybernetica in different servers (links added) * Oct 29, 1996: Feedback (new!) * Oct 21, 1996: Powers' Definition of Control (new!) * Oct 21, 1996: Other Definitions of Control (new!) * Oct 21, 1996: Examples and Counterexamples of Control Systems (empty) * Oct 21, 1996: The Harmonic Oscillator as a Control System (new!) * Oct 21, 1996: Blind control (new!) * Oct 21, 1996: Metalanguages and Metarepresentations (new!) * Oct 21, 1996: Special Cases of Control (new!) * Oct 21, 1996: Control (expanded) * Oct 21, 1996: Editorial Board (update) * Oct 16, 1996: Links on Evolutionary Theory and Memetics (links added) * Oct 7, 1996: Principia Cybernetica Masthead (update) * Oct 4, 1996: The "Global Brain" study group (new!) * Oct 4, 1996: Basic References on the Global Brain / Superorganism (new!) * Oct 1, 1996: Links on Indexes and Encyclopedias (links added) * Oct 1, 1996: Belgium: Overview (links added) * Sep 16, 1996: Editorial Board (photo added) * Sep 16, 1996: F. Heylighen: Biographical Sketch (new photo) * Sep 10, 1996: Welcome to the Principia Cybernetica Web (updated) * Sep 10, 1996: Learning, "Brain-like" Webs (new!) * Sep 9, 1996: Finding words through spreading activation (new!) DISCUSSIONS ON PRNCYB-L The following topics were announced or discussed on the PRNCYB-L mailing list (see http://cleamc11.vub.ac.be/mail.html) during the months of September and October. The full text of all original messages and replies is available via the PRNCYB-L archive: http://www.fmb.mmu.ac.uk/~bruce/PRNCYB-L/thread.html The most important discussions were on the topic of superorganisms, supersystems and metasystems, and on the Robert Rosen's theory as proposed in his book "Life Itself". * analytic and synthetic - Jeff Prideaux * Cortex, or, "what was that?!" - Rick * CFP: 14th Int. Sustainable Development Conference [fwd] - Francis Heylighen * CFP: American Society for Cybernetics Meeting [fwd] - Francis Heylighen * "the pope and evolution" - Hans-Cees Speel * ""rosen and evolution" - Hans-Cees Speel * Re: A hint on discussion about "complexity" - Czeslaw Mesjasz * Funded PhD studentship in applying logic tools for modelling - Bruce Edmonds * "rosen and life itself." - Hans-Cees Speel * meta-system properties 5 (1) - Brown, Alex * A "Systems University on the Net" project asks your comments - Francis Heylighen * Self-Organization of the European Information Society [fwd] - Francis Heylighen * Self-organization and selection in the super-organism - Francis Heylighen * Super-organisms as analogies or metaphors? - Francis Heylighen * Re: super-systems - Mario Vaneechoutte * Internet Conference on Cybernetics and the Humanities - Chris Miles * super systems and grains of sand - Dan Parker * Agent philosophy - Alexander 'Sasha' Chislenko * super-systems, super-systems & co - Paulo Garrido * New Member: Lode Leroy - Cliff Joslyn * New member: Wolfgang Rathert - Cliff Joslyn * New member: Alexander Brown - Cliff Joslyn * New member: Boris Steipe - Cliff Joslyn * New member: Thiery Melchior - Cliff Joslyn * New member: Tom Abel - Cliff Joslyn * New member: Hugo Fjelsted Alroe - Cliff Joslyn * Caracas Conference on Systemics, Cybernetics & Informatics [fwd] - Francis Heylighen * "On the Origins of Cognition" Workshop Announc. & Call - Jon Umerez Urrezola * Thought Contagion: new book on memes [fwd] - Francis Heylighen UNSUBSCRIBING If you want to unsubscribe from this mailing list, please send the following one line message to the address Majordomo@listserv.vub.ac.be unsubscribe pcp-newsSubscription to PRNCYB-L
Author: Cliff Joslyn,
Updated: Aug 2, 1995
Filename: PRNCSUB.html
Name: Email address: URL of home page: Postal address: Phone: Affiliations: How did you hear about PCP? Please take at least one page to describe your work and how it might relate to PCP:PRNCYB-L Subscribers
Updated: Jul 10, 1995
Filename: SUBSCR.html
Nikolai S. Rozov Joseph E. Kerley, III Daniel Spira John Collier Tony Smith Marvin McDonald Dieter Polloczek Luis Rocha Cliff Joslyn F. McClure Alison Brause Walter Logeman Frederick Adams Bruce Schuman Daniel LaLiberte Christopher O. Jaynes Len Troncale Mikhail Leltchouk Valentin Turchin Eric Watt Forste Nils Bundgaard Dr. Elan Moritz Timothy James Faulkner Aykutlu Dane Prof. Dr. E.N. El-Sayed Dr. Marty Cyber Joy L. Ware, PhD Jeff Prideaux Seth Roberts Jixuan Hu Peter Cariani Prof. Jan Sarnovsky Onar Aam George Por Richard Golden Sasha Ignjatovic Luc Claeys Thomas Allweyer Thomas Luparello Jay S. Moynihan Dr. Munawar A. Anees Petr Vysoky Stephen Clark John Welton Arno Goudsmit Naval Deshbandhu Bertin Martens Edward M. Housman T.A. Brown Bruce Edmonds Jose Alvarez G Martin R.J. Cleaver Jan C. Hardenbergh Andreas Schamanek David Warren Martin L.W. Hall Willard Van De Bogart Alexander Chislenko Mark Davis R.M. Holston Paul A. Stokes Gerhard Werner, M.D. Jim Demmers John Earls Mitchell Olson Gabriela Florescu Hans Speel Jon Umerez Alvaro Moreno Felix Geyer Arne Kjellman Mark R. Chandler Edward Stutsman Steve Keen Chuck Henry Gary Boyd Don Mikulecky Robbin R. Hough Martti Arnold Nyman Dr. Markus F. Peschl Francis Heylighen Johan Bollen An Vranckx Jeff Dooley Marshall Clemens Kent D Palmer Ermel Stepp * Total number of users subscribed to the list: 87The following people of the list above have been added during the past year:Daniel Spira Dieter Polloczek F. McClure Walter Logeman Christopher O. Jaynes Aykutlu Dane Dr. Marty Cyber Seth Roberts Prof. Jan Sarnovsky Richard Golden Luc Claeys Thomas Luparello Jay S. Moynihan Dr. Munawar A. Anees John Welton Bertin Martens Edward M. Housman T.A. Brown Bruce Edmonds Martin R.J. Cleaver Jan C. Hardenbergh Willard Van De Bogart Alexander Chislenko R.M. Holston Paul A. Stokes Mitchell Olson Arne Kjellman Edward Stutsman Steve Keen An Vranckx*
PRNCYB-L usage instructions
Author: C. Joslyn,
Updated: Jul 22, 1993
Filename: LISTSV.html Here are some instructions on how to use PRNCYB-L.First, some concepts. LISTSERV is a program which runs under the VM/CMS operating systems on the SUNY machine BINGVMB (note: NOT the machine I'm currently using). BINGVMB can be reached in either BITNET or INTERNET at the following addresses respectively:
BINGVMB.BITNET
BINGVMB.CC.BINGHAMTON.EDU
LISTSERV is responsible for running a number of mailing lists, not just PRNCYB-L. The address of LISTSERV is either:
LISTSERV@BINGVMB.BITNET
LISTSERV@BINGVMB.CC.BINGHAMTON.EDU
while the address of PRNCYB-L is either:
PRNCYB-L@BINGVMB.BITNET
PRNCYB-L@BINGVMB.CC.BINGHAMTON.EDU
By comparison, the address of the CYBSYS-L mailing list for general discussion of systems and cybernetics is either:
CYBSYS-L@BINGVMB.BITNET
CYBSYS-L@BINGVMB.CC.BINGHAMTON.EDU
LISTSERV is responsible for managing both of those, as well as others.
LISTSERV provides two kinds of services for each of the lists it maintains. When a message is sent to PRNCYB-L, then the "mailing list" services are used. Such messages are in turn mailed out to all PRNCYB-L subscribers.
LISTSERV also has "file server" services, where a number of text files are stored for retrieval by members of lists. File server functions are invoked by sending messages to LISTSERV itself, not PRNCYB-L. Such messages are interpreted as commands or requests to LISTSERV, and are parsed and executed appropriately. LISTSERV then will reply with a mail message to you if necessary. Some LISTSERV commands invoke file server functions (e.g. getting a file), while others manage subscription information or other services.
Here are some commands you can use with LISTSERV. Just mail a message to LISTSERV@BINGVMB.BITNET or LISTSERV@BINGVMB.CC.BINGHAMTON.EDU with one or more of these commands included:
HELP Get help INFO Get help GET REFCARD Get a brief help document INDEX PRNCYB-L Get a brief list of files permanently available GET PRNCYB-L FILEINFO PRNCYB-L Get an annotated list of files permanentaly available GET XXXX YYYY PRNCYB-L Retrieve a file on permanent storage, where 'XXXX' is a filename and 'YYYY' is a file type GET PRNCYB-L LOGYYMM PRNCYB-L Retrieve a log of all messages sent to PRNCYB-L for year YY and month MM (e.g. PRNCYB-L LOG9110). REVIEW PRNCYB-L Get a list of all PRNCYB-L members STATS PRNCYB-L Get a list of statistics on PRNCYB-L usage UNSUB PRNCYB-L Unsubscribe from the list (but please don't!)Web Organization
Author: F. Heylighen,
Updated: May 6, 1994
Filename: WEBORG.html The Principia Cybernetica Web follows the standards established for distributed
See also:
"Development and Publication of Systems Knowledge on the Internet: the Principia Cybernetica Web", a paper
New users who don't know about the Project, are advised to start with the general introduction (and possibly with some of the nodes referenced there, for more details). Once acquainted with Principia Cybernetica's general purpose, they can get a quick overview of the present state of the project, and then, depending on their preferences, branch out to study either the project organization and practical management, or its theoretical results, as gathered under the header of Metasystem Transition Theory.
Several navigational aids are available for users with more specific interests. If they are looking for a particular topic they can enter the appropriate keywords in thesearch form. If they would like to know what has been changed since the last time they consulted the Web, they can check the recent additions. If they would like to systematically study the corpus of information, they can consult all entries in the Table of Contents, or by continuously following the "Next" command.
Every node (document or "page") has one (or, rarely, more) "parent" node, which is hierarchically superior to it. Most nodes have in turn a number of "child" nodes, which are hierarchically inferior. Thus, all nodes are uniquely situated in a tree-like classification scheme. For more details about this hierarchical organization, check the Web Structure. For more details about the different elements and fields of a typical node, see the node organization.
denotes a link to an outside document, i.e. not residing on the Principia Cybernetica server. Selecting that link will bring up the document in a new window, while keeping the Principia Cybernetica window open in the background.
You can annotate any node by clicking on the "Annotate" option in the menubar. This will bring up an annotation form where the field for the node to be annotated is already filled in with the filename of the node you started from. You are invited to fill in the other fields of the form. When you have finished, you should click the "submit" button. The text of the annotation is then sent to the server, which passes it on to a specialised application which creates a new document formatted like the other PCP nodes, containing the text of your annotation. The application also adds links to your annotation in the existing document that was annotated, and in the list of all user annotations. Thus, your annotation can be immediately consulted by other users.
After creating the new document the application sends back an acknowledgment, containing a link to the newly created document.
| Important: as the application is rather slow, the connection between server and application sometimes times out. In that case, the server sends an error message to the user. This does not mean that the annotation has failed. Normally, the annotation has effectively been created. If that happens, you should not resubmit the annotation! Otherwise, the same annotation may be added again (and again). Rather, go back to the node you wanted to annotate, and reload the document. Only if after reloading you still don't see a new link to your annotation, should you resubmit the annotation form. |
Since there is as yet no mechanism for editing or correcting annotations, it is best to be very careful when filling in the different form fields, and to reread everything before you submit. If nevertheless a mistake should happen, you can resubmit the corrected version with the word "(corrected)" in the title. The original version with the mistake will then be deleted manually by the Webmaster.
World-Wide Web terminology for hypertext) or "page", containing links to other documents. A node is the
most general entity of Principia Cybernetica, and everything is ultimately a node. The concept is similar to that of an object in
so-called "object-oriented programming'. Objects can contain both data and programs or procedures, and react to 'messages' being sent to them by performing the associated commands. For the simplest type of objects, which contain no procedures (such as hypermedia documents), the only command understood is: show the data (text, graphics, ...) contained. In principle, each node is assigned at least one node type which represent different semantic and pragmatic categories, but this is not really implemented yet. Node types include not only the more traditional elements of textual development (e.g. books, chapters, paragraphs), but also more logical entities (e.g. definitions, expositions, examples, refutations, bibliographic references, descriptions of events), and non-textual entities (e.g. illustrations, diagrams, data sets, sounds).
This most general description of a node, however, is not always the most useful. Indeed, while a most general node type is allowed, most of the textual development in the Principia Cybernetica network will take a similar form, described by the standard node type. Standard nodes will be almost entirely textual, containing the following components:
If there were always just one parent node, the structure would be a pure tree. However such a structure is rather rigid, since it implies that every subject is unambiguously classified as part of a single more general subject. This is a recurrent problem in subject indices, as they are used, for example, in libraries. Should a book on biophysics be classified under "Biology" or under "Physics"? The problem is tackled in PCP Web by allowing multiple classification. For example, the node entitled "Progressive formalization" describes PCP's view of the process of reformulation of scientific models in order to make them more precise. It fits in as well with the theoretical section on epistemology, as with the practical section describing the methods used in the development of PCP's knowledge base. Therefore, the node has two parent nodes.
Still, a tree-like ordering or classification has great advantages in reducing the complexity of the system, since it minimizes the number of paths that lead from one node to another. Moreover, there are theoretical reasons for assuming that hierarchical orderings arise naturally, and therefore provide in general a good description of most systems (see the Principle of Recursive Systems Construction). Therefore, the default is one parent node, and the nodes classified under two (or more) headings remain the exceptions. We call such a structure a loose or "quasi-" hierarchy. Practically, it means that for most nodes there is a single path from the "top" node of the hierarchy (the "Home page" described earlier) via the different children and grand-children down to the node in question.
This quasi-hierarchical ordering is reflected in the Table of Contents: child nodes are distinguished from their parent by one level of right indentation, as is common in "outliner" software. Nodes at the same level have the same indentation. Like in outliners, the "multiple parenting" is represented by simply repeating the description of a node under each of its parents (this is sometimes called "cloning" in outliners).
Of course, the selection of parent or child links is not the only way to navigate from node to node: this would defeat the flexibility characteristic of the hypertext concept. An unlimited number of links to other nodes can be present within the main text of a node, introduced informally by phrases such as "see also" or simply by highlighting a reference or a technical concept, with an included link to the place where it is defined. The parent-child hierarchy, represented by the separate fields, functions as a kind of "skeleton" within the overall, free-form web of links between nodes, allowing an unambiguous localization of each node as a specific subsection of the network.
In addition to the hierarchical ordering, the tree structure entails a linear, sequential ordering of the nodes (listing order in theTable of Contents). This can be interpreted as a suggested reading sequence, (implemented through the "Next" command in the menu bar of each node). Again, this order is merely a kind of default structure, which can be freely ignored. However, for readers wishing to systematically study the corpus of knowledge in Principia Cybernetica Web, the following of this linear path guarantees an exhaustive covering of the material. Moreover, such a path makes it possible to convert the hypertext web to a conventional linear text, which could be printed out as a book. Note that it is possible to create personalized paths, covering different parts in different orders, depending on the preferences of the reader or author.
The following is an overview of the PCP-ftp directories, first the root directory, followed by a list of the contents of the most important subdirectories. Much of the introductory material here is also available in a more handy format (HTML) on the PCP Web, but most of the longer texts (papers, discussions, proceedings, ...) have not yet been reconstructed as hypertext, and are only available here.
Root PCP directoryMisc.Info : contains diverse information (reports, bibliography, ...) on activities related to PCP, such as WWW.
News: contains newsletters and reports on PCP activities.
Nodes: contains preliminary versions of hypertext nodes about basic systems concepts (not in WWW format).
Notes_on_PCP.txt: gives an overview of PCP similar to the one proposed in the Web.
PCP-Web: provides a mirror of the Web on ftp.
PRNCYB-L: contains discussions and lists of members from the PRNCYB-L mailing list.
Papers_Heylighen: contains PCP-related papers by PCP-editor Francis Heylighen.
Papers_Joslyn: contains PCP-related papers by PCP-editor Cliff Joslyn.
Papers_Others: contains PCP-related papers by other contributors.
Papers_Turchin: contains PCP-related papers by PCP-editor Valentin Turchin.
Software: contains some hypertext software (including the "HyperVision" application, a
simple hypertext (not WWW) viewer and editor for MS-DOS, developed by the Walden
programmers group).
Texts_General: contains introductory or overview papers by the editors collectively, and collected contributions of others.
_README.txt: overview of how to use the FTP server.
.
News
Papers_HeylighenCausality as Distinction Conservation : a theory of predictability, reversibility and time order
Cognitive Levels of Evolution: pre-rational to meta-rational
A Cognitive-Systemic Reconstruction of Maslow's Theory of Self-Actualization
Fitness as Default: the evolutionary basis of cognitive complexity reduction
Formality of Languagei: definition and measurement; II: linguistic, situational and personality variable correlated with formality>
Design of a Hypermedia Interface Translating between Associative and Formal Representations
Selection Criteria for the Evolution of Knowledge
Making Thoughts Explicit: advantages and drawbacks of formal expression
Evolution, Selfishness and Cooperation; Selfish Memes and the Evolution of Cooperation
Modelling Emergence
Classical and Non-classical Representations in Physics I
Classical and Non-classical Representations in Physics II: quantum mechanics
Self-Organization, Emergence and the Architecture of Complexity
Structuring Knowledge in a Network of Concepts
Principles of Systems and Cybernetics: an evolutionary perspective
Unifying Cybernetics: intro to PCP
List of Publications F. Heylighen
Papers_JoslynJoslyn's homepage )
Control Theory and Cybernetic Ontology(tex)
Semantics of Entropy(tex)
Feasibility_Study_PCP.txt
Software for Philosophy
Papers_OthersGlueck: the requirement of Identical Variety
Maddock: Dialectical Ecology
Umerez, Moreno: Emergence and Functionality
Papers by V. TurchinThe Ultimate Reality of Physics:
an essay in metaphysics (tex)
Cybernetic Epistemology.tex
Cybernetic Ontology.tex
Cybernetics and Philosophy(tex)
Dialog on Metasystem Transitions
Science and Values
PRNCYB-L discussionsaging & Evolution
Causality & Invariance
Default Reasoning & Control
Entropy & Evolution
Formal expressions
Information & Meaning
Memes & Cooperation
Memes in Cyberspace
Memetic fitness criteria
PRNCYB-member
Stability & Change
Autopoiesis & Distributed (superposition) Representations
Definition of Control according to Powers and Boyd
Life, Symbols (coding) & Control
Memetics & Dialectics
Power, knowledge & perspectivism
Requisite Variety, Complexity & the edge of Chaos
Texts_GeneralAbstracts Symposium New York (1989)
Abstracts Symposium Namur (1992)
The Cybernetic Manifesto
Definition of Systems Theory
Joslyn, Heylighen & Turchin: Long Introduction to the Principia Cybernetica Project.tex
Heylighen & Bollen: Development and Publication of Systems Knowledge on the Internet: the Principia Cybernetica Web
PCP bibliography
Short Introduction to PCP
Synopsis of PCP
Preface
Inititally submitted abstracts of papers
An Integrative View of Meta System Transition
Metasystem Transitions in Computer Science and Mathematics (rtf format)
(Meta)systems as Constraints on Variation: a classification and natural history of MST's
Selection of Organization at the Social Level: obstacles and facilitators of MST's
Semantic Control Systems (tex format)
Semantic Control Systems (tty (text like) format)
Metasystems, Memes and Cybernetic Immortality
The origins of purpose: the first metasystem transitions
A Dialogue on Metasystem Transition (part 2) (tex format)
Origin of Life as the First Mst.- Control Hierarchies and Interlevel Relation
Photo: discussion at the 1st Principia Cybernetica Workshop (Brussels, June 1991); from left to right: Harry Bronitz, Gordon Pask (background), J.L. Elohim (foreground), Robert Glueck, Ranulph Glanville, Annemie Van Kerkhoven, Don McNeil, Elan Moritz, Cliff Joslyn, A. Comhaire, Valentin Turchin.
PCP regularly organizes conferences or meetings. Until now there have been :
Abstracts of papers that were presented.
report or for the Abstracts of papers that were presented.
Call for Papers.
as part of the conference:
An interdisciplinary reflection on science, nature, human action and society
A symposium organized by the Principia Cybernetica Project (PCP) was held as part of "Einstein meets Magritte", a large interdisciplinary conference at the Free University of Brussels. After the organization of several other symposia, this was the fifth official meeting of the Project. The theme was the contribution that theories of evolution and self-organization, on the one hand, and systems theory and cybernetics, on the other hand, can make to the development of an integrated world view.
The basic idea underlying PCP is that evolution leads to the spontaneous emergence of systems of higher and higher complexity or "intelligence": from elementary particles, via atoms, molecules, living cells, multicellular organisms, plants, and animals to human beings, culture and society. This historical development can be understood with the help of concepts such as self-organization, selection, adaptation, variety, chaos, hierarchy, autonomy, control, cognition, and metasystem transition.
This perspective makes it possible to unify knowledge from presently separate disciplines: physics, chemistry, biology, psychology, sociology, etc. We thus wish to revive the transdisciplinary tradition of General Systems Theory, by adding recently developed insights around evolution and complexity. The resulting scientific/philosophical framework should provide us with an answer to the basic questions: "Who are we? Where do we come from? Where are we going to?"
The above introductory text was distributed world-wide via a Call for Papers. Out of some 45 submissions, 30 abstracts were selected for presentation. The contributors presented a wide range of disciplinary and cultural backgrounds, illustrating the full breadth of the subject domain. A bibliography on this domain was compiled on the basis of the submitted lists of references. For a report of the Symposium, check my impressions as a chairman.
At the moment, we are collecting the full texts of the papers that were presented, making them available on the Net. They will be published as one of the 8 Proceedings volumes for the Einstein meets Magritte Conference. The probable reference will be: F. Heylighen & D. Aerts (eds.) (1996): The Evolution of Complexity (Kluwer, Dordrecht).
Below you will find the abstracts of papers that were presented or accepted for presentation (* means that a full paper is available, linked to the abstract).
Photo: H.C. Speel in action at the Symposium
full paper)
Partial Comprehension in a Quasi-Particulate
Universe"* (late entry, not refereed for this Symposium)
Lest We Forget Our Inheritance * (presented in different symposium but to be included in the Proceedings of this symposium)
J.P. Crutchfield University of Vienna, Vienna, Austria
A symposium organized by the Principia Cybernetica Project (PCP)
will be held at EMCSR'96. Chairs are Francis Heylighen and
Stuart Umpleby. The objective is to better understand the implications of the present explosive growth in global computer networks, like the Internet or the World-Wide Web. We wish to develop models of how these networks will further develop and how they will affect individuals and society at all levels.
Soon, the whole of human knowledge will be directly available to every person with access to a networked computer. Moreover, communication between individuals will become much easier, faster and more transparent, transcending the boundaries of space and time. The changes will not only be quantitative, but qualitative: "smart" computer systems will not only provide more information more quickly, but allow novel applications (virtual reality, intelligent agents, distributed processing, automated indexing...) that no one ever would have dreamt of. These changes will affect and deeply transform all aspects of society: education (distance learning, electronic universities), work (telework, groupware), commerce (electronic cash), the media, government (electronic democracy), health, science (electronic publication) and technology. It seems as though society's collective intelligence will increase manifold, perhaps producing an evolutionary transition to a higher level of intelligence.
As these developments are so fast, and so difficult to predict, precise models are usually not possible. In that case, comprehension may be helped by using analogies. Examples of such metaphors for global network functions are the "Information Superhighway", which emphasizes the speedy channels along which information moves, the network as a "Super-brain", which emphasizes the collective intelligence of users and computers connected by the global network, Jacques Vallée's notion of an "information singularity", which notes that networked information becomes
instantaneously available everywhere (see also Vernor Vinge's concept of singularity), and "Cyberspace" itself, which visualizes networked information as an immense space through which one can "surf".
Though metaphors can be very useful, they generally only express one or a few dimensions of a multidimensional phenomenon. Therefore, we should move to more detailed and comprehensive models, which can be tested by observation, implementation or simulation. Cybernetics, as a theory of communication, information and control, seems most directly applicable to such model-building, but valuable insights may come from the most diverse domains: sociology, futurology, AI, complex systems, man-machine interaction, cognitive psychology, etc. Our emphasis is on concepts, principles, and observations, rather than on technical protocols or specific implementations (although existing systems may provide a concrete illustration from which more general implications can be derived).
EMCSR'96 announcement for more details, and a registration form for the conference.
The complete conference program can be found here. The following papers will be presented at this Symposium (links go to the abstracts):
full paper)
full paper in PostScript)
Global Brains and Communication in aComplex Adaptive World
Networking in the Mind Age
Roy Ascottas part of the
University of Vienna, Vienna, Austria
A symposium organized by the Principia Cybernetica Project (PCP)
will be held at EMCSR'96. Chairs are Francis Heylighen and
Stuart Umpleby. The objective is to better understand the implications of the present explosive growth in global computer networks, like the Internet or the World-Wide Web. We wish to develop models of how these networks will further develop and how they will affect individuals and society at all levels.
Soon, the whole of human knowledge will be directly available to every person with access to a networked computer. Moreover, communication between individuals will become much easier, faster and more transparent, transcending the boundaries of space and time. The changes will not only be quantitative, but qualitative: "smart" computer systems will not only provide more information more quickly, but allow novel applications (virtual reality, intelligent agents, distributed processing, automated indexing...) that no one ever would have dreamt of. These changes will affect and deeply transform all aspects of society: education (distance learning, electronic universities), work (telework, groupware), commerce (electronic cash), the media, government (electronic democracy), health, science (electronic publication) and technology. It seems as though society's collective intelligence will increase manifold, perhaps producing an evolutionary transition to a higher level of intelligence.
As these developments are so fast, and so difficult to predict, precise models are usually not possible. In that case, comprehension may be helped by using analogies. Examples of such metaphors for global network functions are the "Information Superhighway", which emphasizes the speedy channels along which information moves, the network as a "Super-brain", which emphasizes the collective intelligence of users and computers connected by the global network, Jacques Vallée's notion of an "information singularity", which notes that networked information becomes
instantaneously available everywhere (see also Vernor Vinge's concept of singularity), and "Cyberspace" itself, which visualizes networked information as an immense space through which one can "surf".
Though metaphors can be very useful, they generally only express one or a few dimensions of a multidimensional phenomenon. Therefore, we should move to more detailed and comprehensive models, which can be tested by observation, implementation or simulation. Cybernetics, as a theory of communication, information and control, seems most directly applicable to such model-building, but valuable insights may come from the most diverse domains: sociology, futurology, AI, complex systems, man-machine interaction, cognitive psychology, etc. Our emphasis is on concepts, principles, and observations, rather than on technical protocols or specific implementations (although existing systems may provide a concrete illustration from which more general implications can be derived).
announcement for more details, and a registration form for the conference.
The complete conference program can be found here. The following papers will be presented at this Symposium (links go to the abstracts):
full paper)
full paper in PostScript)
Global Brains and Communication in aComplex Adaptive World
Networking in the Mind Age
Roy Ascott
as part of the
15th International Congress on Cybernetics
NAMUR (Belgium), August 24-28, 1998
The Journal of Memetics - Evolutionary Models of Infromation Transmission, in collaboration with the Principia Cybernetica Project, has decided to organize a first symposium on memetics. The aim of the journal is to integrate the different approaches inspired by memetics, and thus try to establish memetics as a recognized scientific field. The symposium similarly wishes to bring together all researchers working on memetics, in order to allow them to meet face to face, thus stimulating discussions and possible collaborations. The symposium is chaired by two members of the Journal's editorial board, Francis Heylighen and Mario Vaneechoutte. The emphasis will be on discussion, rather than on formal presentation.
In 1976, Dawkins invented the word 'meme,' in analogy with the word 'gene', defining it as 'a unit of cultural transmission, or a unit of imitation'. Thus, he defined the field of memetics, which studies the development and spread of culture and information, on the basis of the Darwinian principles of variation, reproduction and natural selection. Further information on memetics is available through the journal's web server:.
The initial description of 'meme' by Dawkins is rather vague, which is a possible reason for current diverging views on what a meme really is, and how the memetic model can be used. We are confronted with an avalanche of books, essays, and publications scattered over different journals and disciplines, with dialogue flashing up here and there in an unstructured manner. This chaos exists because a general framework is lacking.
The journal of memetics, and the symposium it organizes, aims to tackle this problem. We seek to discuss issues concerning memetics such as:
The following contributions were initially accepted for presentation:
For accepted papers, the full text of the paper, which must not exceed 6 typed, single-spaced pages, is to be sent by postal mail to the congress secretariat before May 31, 1998.
All papers that are personally presented by the author at the congress will be published in the congress Proceedings. The authors of the best papers will be invited to publish an extended version in the Journal of Memetics. Researchers who cannot participate in the symposium are still invited to directly submit a full paper for publication in the Journal to the managing editor (see the information for authors).
The 15th International Congress on Cybernetics will be held from August 24 to 28, 1998, in Namur (Belgium) at the Institute for Computer Sciences (see "how to get to the institute") of the University of Namur. The International Congresses on Cybernetics are organized triannually (since 1956) by the International Association for Cybernetics (IAC). The interdisciplinary domain of cybernetics, which is closely related to memetics, addresses subjects such as information, communication, organization, intelligence, complex systems, and feedback loops.
Namur is a quiet little city on the confluence of the Meuse and Sambre rivers, at the foot of a hill supporting the impressive medieval Citadel (see photo). Its charming old streets offer plenty of restaurants and cafes. It is situated at an hour's drive by car or train from Brussels, the capital of Belgium and of the European Union, at the border of the beautiful forested region of the Ardennes (see touristic information for Namur).
The congress atmosphere is relaxed and informal, with several symposia going on in parallel in adjacent rooms. Lunches can be taken at the "Arsenal" university restaurant, in a renovated medieval hall. The congress normally includes a congress dinner, an excursion, and a meeting room for coffee breaks. Participants are responsible for making their own hotel reservations, but good quality and inexpensive accomodation in students' rooms will be available. Info about accomodation, including a list of hotels , will be sent to all those who register at the congress secretariat. (see also: hotels in the Province of Namur)
The official languages of the Congress are English and French (the memetics symposium will be exclusively in English).
ALGOUD Jean-Pierre (France), ANDONIAN Greg (Canada), ANDREEWSKY Evelyne (France), BERGER Rene (Switzerland), BETTA Jan (Poland), BOUCHON-MEUNIER Bernadette (France), BOURLARD Herve (France), BRIER Soren (Denmark), BUI Tung (USA), CARON Armand (France), DUBOIS Daniel (Belgium), FERRARI Domenico (Italy), FOMICHOV Vladimir (Russia), FRANCOIS Charles (Argentina), FRANK Helmar (Allemagne), HAKEN Hermann (Germany), HORNUNG Bernd (Germany), JDANKO Alexis (Israel), JEAN Roger (Canada), LASKER George (Canada), LASZLO Ervin (Italy), MARUYAMA Magoroh (Japan), MINNAJA Carlo (Italy), MORIN Edgar (France), NUNEZ E.A. (France), RAMAEKERS Jean (Belgium), SCHWARZ Eric (Switzerland), STEG Doreen (USA), STEWART J (U.K.), VALLEE Robert (France), WARBURTON Brian (U.K.).
Chairpersons:Topics
The registration fee covers participation in the Congress, the preparatory documents, a reception, the coffee-breaks and the Proceedings for the authors.
| Before April 30, 1998 | After April 30, 1998 |
| 11 000 BEF | 14 000 BEF |
| (about $295) | (about $375) |
Special conditions for young researchers under 30 years (on presentation of a certificate issued by their university) (does not include the Proceedings) | |
| 4 000 BEF | 5 000 BEF |
(1$ = about 37 BEF -see Belgian Franc exchange rates)
Payment can be made as follows :
For further information about the scientific program of the memetics symposium contact the symposium chairs:
Mario Vaneechoutte (submissions)
Laboratory Bacteriology & Virology Blok A
De Pintelaan 185
University Hospital Ghent
9000 Ghent, Belgium
Phone +32-9-240 36 92
Fax +32-9-240 36 59
E-mail Mario.Vaneechoutte@rug.ac.be
Francis Heylighen
Center "Leo Apostel" Free University of Brussels
Pleinlaan 2 B-1050 Brussels, Belgium
Phone +32-2-644 26 77
Fax +32-2-644 07 44
For registration, payment, or further information (accomodation, fees, etc.) about the congress, contact the congress secretariat, using the registration form below:
Congress Secretariat
International Association for Cybernetics
Palais des Expositions, avenue Sergent Vrithoff 2
B-5000 Namur, Belgium
Phone: +32-81-71 71 71
Fax: +32-81-71 71 00
Email: Cyb@info.fundp.ac.be or sri@bepn.namur.be (Carine Aigret)
15th Int. Congress on Cybernetics (Namur, 24-28 August, 1998)
Name : .......................................................
First name :..................................................
Profession and titles:........................................
Institution: .................................................
..............................................................
Address : ....................................................
..............................................................
..............................................................
Phone : ....................................................
Fax:..........................................................
E-mail :......................................................
o I would like to receive more information about the Congress
o I would like to attend the Congress
o I intend to present a paper to the following symposium :
..............................................................
..............................................................
Title of Paper :.............................................
..............................................................
Date : Signature:
___________________________________________________________________
Several publications devoted to PCP are available, and more are planned. The titles with links below are directly connected to draft versions of the paper on FTP (mostly ASCII or TEX format), or on WWW. Reprints of papers can also be requested from their respective authors.
This booklet (70 pages) contains short articles and abstracts presented at the Workshop in Brussels. Paper copies are available from F. Heylighen.
This volume is an edited collection of papers by invited authors on the Theory of Metasystem Transitions.
Finally, many of the ideas underlying PCP can be found in two books written well before PCP was founded:
Cybernetic theory of universal evolution, from unicellular organisms to culture and society, based on the concept of the Metasystem Transition.
Interpretation of (Soviet) totalitarianism from the perspective of cybernetic social theory.
| Synopsys: | Gordon and Breach Science Publishers, New York) (special issue, Vol. 45:1-4, of "World Futures: the journal of general evolution). |
(part 2) (tex format)), p. 5
(Meta)systems as Constraints on Variation: a classification and natural history of MST's), p. 59
The origins of purpose: the first metasystem transitions), p. 125
Origin of Life as the First Mst - Control Hierarchies and Interlevel Relation), p. 139
An Integrative View of Meta System Transition), p. 173
Metasystems, Memes and Cybernetic Immortality), p. 181
Selection of Organization at the Social Level: obstacles and facilitators of MST's), p. 181
Metasystem Transitions in Computer Science and Mathematics (rtf format)), p. 213
The major steps in evolution, such as the origin of life, multicellularity, or the origin of thought, can be viewed as large scale metasystem transitions. Thus, the history of life and the universe can be conceptualized as a (branching) sequence of MSTÍs, leading to ever more complex, adaptive, and intelligent systems: from atoms and molecules, to dissipative structures, cells, multicellular organisms, organisms capable of movement or learning, and finally to human culture (as the provisionally highest level). MST Theory (MSTT) can also be used to make predictions about the future, thereby helping us to anticipate the next level of organization to which we are evolving.
We felt it appropriate to bring together the latest ideas about MSTT developed within the Principia Cybernetica Project and a number of related ideas by other researchers. Therefore, we decided to edit a major collection of papers on the theory, with contributions from ourselves as well as from invited authors. World Futures, which "is dedicated to the study of general patterns of change and development, in nature as well as society, and to evolutionary processes, with special attention to multidisciplinary approaches", seemed the perfect venue for the publication of a collection on such a wide-ranging subject with essential implications for our evolutionary future.
Although the MST concept has shown its explanatory and unifying ability in many domains, several basic questions about MST Theory remain to be addressed. Furthermore, in parallel with Turchin, other researchers have developed similar schemes for analysing evolutionary levels (without focusing on the process of the emergence of a new level). For example, William Powers (1973) has proposed a hierarchy of control levels, and Donald T. Campbell (1974) has introduced a nested hierarchy of vicarious selectors. Our intention was to start a dialogue among these different approaches, and to move towards resolution of the remaining incompleteness and inconsistencies.
This required the clarification of the basic concepts and principles needed to understand levels of organization (e.g., system, control, constraint, variety, hierarchy, model) and the evolutionary transitions between them (e.g., self-organization, emergence, blind variation, selective retention, and the MST itself). Moreover, we wanted to show some of the applications of MST Theory, such as supercompilation in computer science, and the evolution towards future "cybernetic immortality". Although there is as yet no consensus on many of these topics, we hope that this collection of papers provides a least a clear overview of the main issues and the different approaches to this fascinating new domain.
The collection starts (appropriately enough) with a paper by Turchin, the originator of the theory. In the form of a dialogue between himself and an imaginary discussant, he outlines the theory, expounds the main philosophical assumptions underlying it, and answers some common objections. The two subsequent papers, by the other editors of this collection, attempt a more formal and systematic analysis of some of the fundamental concepts. Heylighen develops a classification and definition of supersystem, metasystem and metasystem transition (which is in some respects different from TurchinÍs), and uses it to analyse the most important MST's in the history of evolution. Joslyn then develops some fundamental ideas logically prior to the MST, including the concepts of "system" and "control", the essential role of semantics in control, and the various roles played by "distinction", "constraint", "variety", and other systems theoretical concepts.
Powers opens the series of invited papers by applying ideas from his own Perceptual Control Theory (Powers, 1973) to conceive of a possible, feedback-based scenario for the origin of life, which is also the origin of control systems, and thus a primary MST. Jon Umerez and Alvaro Moreno give an overview of developments in theoretical biology and systems theory parallel to MST Theory, and discuss some difficult philosophical questions about interlevel relations, similarly focusing on the origin of life. Charles François proposes a number of concepts developed outside MST Theory which may help to better understand the MST concept, and discusses the on-going MST in human society as a possible application. Elan Moritz similarly applies MST Theory, in conjunction with memetics (the theory of memes), to discuss the possible evolution of cybernetically immortal "beings". Heylighen and Campbell survey the evolution of social control mechanisms, with the aim of better understanding the patterns of cooperation and competition between selfish individuals, and the MSTs shaping present society. Finally, Robert Glueck and Andrei Klimov review the applications of MST Theory in computer science and mathematics, which are based on the technique of metacomputation: the manipulation of programs (linguistic models) by other (or the same) programs.
Inertia of Fear and the Scientific Worldview, Columbia University Press, New York
order a copy from the Amazon web bookshop.This is the first book to introduce the ideas of Metasystem Transitions Theory. It is directed at a broad, non-specialised public, and requires not more than high school mathematics. It discusses the evolution of humanity, starting from the first living cells up to human culture and science. It shows how the great advances in intelligence and cognition, from simple reflexes, to learning, thought, mathematical reasoning and the most advanced realms of metascientic analysis, can be understood as metasystem transitions, in which a higher level of control emerges. Its originality lies in the integration of a cybernetic analysis of knowledge with the trial and error process of natural selection, which creates ever higher levels in the hierarchical organization of mind.
Prof. Valentin Turchin, a cyberneticist, computer scientist and physicist, started his research career in the Soviet Union, but presently teaches at the City College of the City University of New York (see his biography). He is a founding editor of the Principia Cybernetica Project.
The "Phenomenon of Science" first took shape during the 1960's in Russia. The original manuscript was positively evaluated by Soviet reviewers, but was finally rejected for publication because of the dissident political activities of its author. Happily, the Russian manuscript got to the West where it was translated and published by Columbia University Press, at about the same time that its author was forced to emigrate to the USA.
Although the original text is almost 30 years old, this visionary document is still highly relevant to our present situation and state of knowledge. It is particularly recommended to people who wish to understand the basic ideas behind the Principia Cybernetica Project. As such it is complementary to another book published on Principia Cybernetica Web, Joël de Rosnay's "The Macroscope". Whereas "The Macroscope" applies the concepts of systems theory and cybernetics synchronically, to get a large scale picture of the world in which we live, "The Phenomenon of Science" uses these concepts diachronically, to understand its historical development.
The present document proposes a highly condensed view of the goals, results and organization of the Principia Cybernetica Project, mainly for people who already have an idea of what this is all about. For more background and motivation, check the Introduction and the project's History. For a comprehensive list of available material, check the Table of Contents.
The Principia Cybernetica Project (PCP) is a collaborative, computer-supported attempt to develop a complete cybernetic and evolutionary philosophy. Such a philosophical system should arise from a transdisciplinary unification and foundation of the domain of Systems Theory and Cybernetics. Similar to the metamathematical character of Whitehead and Russell's "Principia Mathematica", PCP is metacybernetical: cybernetic tools and methods are used to analyze and develop cybernetic theory (see our methodology).
hypertext, electronic mailing lists, electronic publishing (FTP and WWW servers), and software for knowledge structuring and self-organizing, "learning" hypertext . They are meant to support the process of collaborative theory-building by a variety of collaborators, with different backgrounds and living in different parts of the world. PCP will thus naturally develop in the cyberspace of interlinked electronic networks, as implemented in the World Wide Web distributed hypermedia environment.
The PCP philosophy, which we call "Metasystem Transition Theory", is systemic and evolutionary, based on the spontaneous emergence of higher levels of organization or control (metasystem transitions) through blind variation and natural selection. It includes:
hypermedia/email implementation, constituting the form of the project, are in fact closely connected. Both are constructive,
in the sense that they start from "primitive" systems from a variety
of origins (nodes containing expositions written by diverse
participants), which are brought into contact (email conversations , and links to shared files), connected (semantic links), and selectively stabilized, so as to retain those
combinations which define a new, more integrated system. When constructing a cybernetic philosophy the fundamental building blocks that we need are ideas: concepts and systems of concepts. Ideas, similarly to genes, undergo a variation-and-selection type of evolution, characterized by mutations and recombinations of ideas, and by their spreading and selective replication or retention. Ideas that are replicated when they are communicated from one person to another one are called "memes". The basic methodology for quickly developing a system as complex as a cybernetic philosophy would consist in supporting, directing and amplifying this natural development with the help of cybernetic technologies and methods.
It will require, first, a large variety of concepts or ideas, provided by a variety of sources: different contributors to the project with different scientific and cultural backgrounds. Second, we need a practical tool for representing and manipulating these concepts: the computer. Third, we need a system that allows the representation of different types of combinations or associations of concepts. Fourth, we need selection criteria, for picking out new combinations of concepts, that are partly internal to the system, partly defined by the needs of the environment of people that are developing the system. Finally, we need procedures for reformulating the system of concepts, building further on the newly selected recombinations, with the help of the concepts of emergence, and especially of metasystem transition.
Photo: the editorial board at their 1996 meeting in Washington DC, from left to right: Turchin, Joslyn, Heylighen, Bollen
The Principia Cybernetica project is managed by a Board of Editors. The Board is responsible for the collection, selection and development of the material, and for the implementation of the computer system. The Board's work is supported by the editorial assistants, Johan Bollen and Alex Riegler. All inquiries or proposals about PCP should be directed to one of the editors below:
Fax: +32-2-629 24 89
Email: fheyligh at vub.ac.be
Joslyn
Email: joslyn@lanl.gov
Email:csvft@css3s0.engr.ccny.cuny.edu
Photo: the editorial board at their 1991 meeting in Brussels, from left to right: Joslyn, Turchin, Heylighen
in the context of their historical development. While we hope that actual progress can be made through the elimination of incoherent or anachronistic usages, it may be that a simple listing of the various senses will be required. If one contributor asserts "P", and another "not P", and no further progress can be made, then in the worst case a kind of "null consensus" can be achieved by including "P or not P" in the project. At the very least the different conditions under which these usages arise should be described. At best one usage would be eliminated.
Nodes of the project will be in one of the following categories:
search on the above keywords with Lycos. (Don't be surprised to find mostly references to Principia Cybernetica itself). Readers are encouraged to add further links to related servers, by making an annotation to the best suited page.
General Systems Theory and Earth Science: an introduction to systems thinking
Advances in Systems Science and Applications: electronic journal from the International Institute for General Systems Studies
Institute of Systems Science, with free software for Computer-Aided Systems Theory (CAST)
International Institute for Applied Systems Analysis (also:
Gopher server)
International Institute for General Systems Studies
Systems Dynamics Group and its System Dynamics in Education Project, led by Jay Forrester
Institute for Systems Research (engineering) at Harvard
Decision Analysis and Operations Research on the Web
Whole Systems: a more New Age style application of systems thinking
Selected References to Systems Research on the Web (mostly the same as on this page)
Systems and Cybernetics page
Cybernetics and Systems page
Systems Science PhD Program
Institute for Operations Research and the Management Sciences
International Council for Systems Engineering
Systems Science and Mathematics at Washington University
Center for Systems Science
Center for Systems Studies, Univ. of Hull
Systems Science and Industrial
Engineering Department at Binghamton University, led by G. Klir, see also the old page
Antioch Whole Systems Design Home Page
Institute for Systems Research (ISR)at the Univ. of Maryland
The Institute for Integrative Studies at George Mason University, headed by John Warfield
Systemic University on the Net (SUN): development and teaching of Systems Dynamics concepts
page on Living Systems Theory
Mundi Causa Society, for the advancement of Societal Systemics, organizes email discussion workshops on global social and economic problems
Cybernetics, Systems Theory and Complexity
Intelligent Systems and their Societies : an introductory e-book by Walter Fritz
The Systems' (R)evolution: Ramon Noguera's collection of links on Systems Theory, Social Evolution, and World Politics
Cybernetics in the WWW Virtual Library
Department of Medical Cybernetics and Artificial Intelligence at the University of Vienna with a possibility for searching in a library database containing extensive literature on cybernetics and systems theory
American Society for Cybernetics with information on history, cybernetic thinkers, journals, associations, etc., and its new home page
UCLA Cybernetics Program
Institute for Cybernetics and Systems Theory, Bochum, Germany, working in second-order cybernetics
Cybernetics Research Consortium: consulting and research
Control System Group, developing W.T. Powers's Perceptual Control
Theory of behavior; see also their
newsgroup bit.sci.purposive-behavior, gopher server, and FTP
archive
Department of Cybernetics at the University of Reading (UK)
Systems and Control Engineering
Systems and Control Archive
Association for Cybernetics Research / AI Lab at Oakland University
Self-Organization, Autopoiesis, and Enterprises: an excellent introduction to Maturana and Varela's theory of autopoiesis by Randall Whittaker
The Observer Web, another excellent collection of material collected by R. Whittaker
Bacterial Cybernetics Group, headed by Eshel Ben Jacob at the University of Tel-Aviv: self-organization and cooperation in bacterial colonies
George Kampis
Elin Whitney-Smith
Stefan Maier
Luis Rocha
Martin Hall's Eclectic & Eccentric Home
Page
Howard
Pattee
Gary Cziko
Bruce Edmonds
Page
Hans-Cees
Speel
Jixuan Hu
Stuart
Umpleby
Eric Minch
Onar Aam
Paul Pangaro's home page with applications and history of
(2nd order) cybernetics, including his work with Gordon Pask and others
Prof. Franz Pichler
Dr. Herbert Praehofer
Robert E. Ulanowicz -- Chesapeake Biological Lab, U Maryland
Charles Henry -- Director of the Libraries, Vassar College
George Klir
Robert
Trappl -- U Vienna
Moore's Laws of Bureaucracy: a humorous use of cybernetics to prove that bureaucracies are ineffective
Entropy and Information Theory on the Web: background material on one of cybernetics' fundamental concepts
International Society for
Bayesian Analysis (ISBA)
The Bucky
Fuller Virtual Institute
The Probability Web: Probability links
A-Quarium
WorldGame Institute
Michael Trick's Operations
Research Page
Notational Engineering
Laboratory Home Page: study of sign systems
General Information on Biosemiotics, with lots of interesting links
Serendip Home Page: notes and demonstrations on unexpected phenomena related to brain and behavior (Prisoner's dilemma, blind spot, etc.)
CalResCo, an extensive website about complexity, self-organization and related subjects, including a self-organizing systems FAQ
Complex Adaptive Systems and Artificial Life: an extensive list of links including conferences
complexity page, including a complexity dictionary
Evolution of Complex Systems: Umur Ozkul's collection of thoughts, essay and links
Complexity Online: a quite elaborate server with Hypermedia papers and pointers to other places
Complexity International: refereed electronic journal on Complex Systems Research
Complex Adaptive Systems in different parts of the Internet
Bibliography on Measures of Complexity
Santa Fe Institute for the Sciences of Complexity (ftp-server)
Science on the Edge of Chaos: an interactive multimedia service on complexity and chaos including a series of TV programmes
Nonlinearity and Complexity home page at Democritus University of Thrace
Center for Complex Systems Research
Australian National University Bioinformatics
Non-linear Science E-print archive with papers and conference announcements on chaos, adaptation, self-organization etc.
Complex Systems Links on the Web
Complexity, Complex Systems and Chaos: @Brint (Business & Technology Research)
resources relevant to the journal "Complexity"
Self-organizing systems Home page (mostly about cybernetic philosophy)
Complexity discussions from the point of view of constructivism and Robert Rosen's theories
Complex Systems research: an extensive list of links
Parameterized Complexity Home Page -- Todd Wareham, U Victoria
Complexity Home Page at Virginia Commonwealth University
Bayesian Theory As Extended Logic -- Ed Jaynes
An Introduction to Synergetics
Chaos, Complexity, and Everything Else: a long list of links on chaos, complexity,
artificial inteligence, genetic algorithms, and fractals
New England Complex Systems Institute, including the self-organizing, peer-reviewed Interjournal
Complex Adaptive Systems in Finance and strategy, by Mark White
Artificial Life Online service with lots of info (news, bibliography, journals, ...)
The New Alife Database: Searchable Database of Alife-Related Sites Gathered by a Search Bot
An evolutionary approach to synthetic biology (paper on artificial life)
Evolutionary and Adaptive Systems research at the University of Sussex
Illinois Genetic Algorithms Lab
Interactive genetic art (evolves according to user preferences)
Genetically programmed music
FAQ's on Genetic Algorithms
Artificial Life ftp server
Karl Sims' Virtual Creatures: 3D, animated "life forms", developed through simulated evolution
CWRU Autonomous Agents Research Group
MIT Media Lab Autonomous Agents Group, headed by Pattie Maes
Intelligent Software Agents
Intelligent Software Agents
Dep. of Theoretical Biology, with research on systems theory of evolution, alife, constructivism, cognition and evolutionary epistemology
Boids
, Flocks, Herds, and Schools: a Distributed Behavioral Model
Swarm Web Pages
Liverpool Biocomputation Group (Announcements)
bibliography on Artificial Life
Center for Adaptive Systems
Evolutionary Systems and Artificial Life: lecture notes by Luis Rocha
Bibliography of Alife publications: a very rich collection of online papers, maintained by Ezequiel Di Paolo, covering topics such as complexity, self-organization, evolution, social behavior, robotics, etc.
Biota.org: an organization stimulating the development of digital tools and environments for the study of living systems, with impressive visual and virtual reality examples of digital organisms
Cognitive Science Eprint Archive: a large and growing collection all possible cognitive science preprints and published papers
Knowledge Science Institute (and the Int. J. Human-Computer Interaction)
Dictionary of Cognitive Science
Computational Epistemology Lab, headed by Paul Thagard, with research on coherence, cognition and philosophy of science
Psycoloquy : electronic journal on psychology and cognitive science (keyword search of articles) and papers by its editor, Stevan Harnad
Behavioral and Brain Sciences: archive of the journal with open peer commentary on cognitive and biobehavioral issues
Center for Research on Concepts and Cognition
Laws of Form": a calculus of distinctions
Enactive Cognitive Science & Autopoiesis (including the archive of "The Observer" newsletter)
Semantic Network Processing System (SNePS) group at SUNY Buffalo
Cognitive Science Research Papers from the School of Cognitive and Computing Sciences at the University of Sussex
Cognitive Science Society
Human Cognition Research
Laboratory at the UK's Open University
American Psychological Society
Cognitive and Psychological Sciences on the Internet
ChaoPsyk Browser: society for Chaos Theory in Psychology and the Life Sciences
PSYCHE: an interdisciplinary journal of research on consciousness
Center for the Study of Language and Information in Stanford
resources for Cognitive Science research
Human Behavior and Evolution Society: evolutionary psychology
Psychology, Culture and Evolution
Engineering Laboratory: Home Page
Association for Computational Linguistics
Ecology of mind: Vincent Kenny's page on thinkers connecting ecology with psychology
Knowledge Systems Laboratory with lots of interesting stuff, including the Knowledge Sharing Technology Project with a library of ontologies
Journal of Artificial Intelligence Research (all papers freely available over the Internet)
PEIRCE: developments around conceptual graphs, a graphical, logic-based knowledge representation system
Informatica" publishing papers on cybernetics, AI, and computer science from an interdisciplinary perspective
Artificial Intelligence Repository with files, programs, texts, etc.
Fuzzy Logic and Neurofuzzy resources page
The CYC project: construction of a huge database of formal rules covering all every-day knowledge, as a foundation for intelligent systems capable of common-sense reasoning (led by Douglas Lenat); see also the CYC FAQ
The Data Mine and KD mine: info about knowledge discovery in databases
Machine Learning resources
MLnet Machine Learning
Archive at GMD
"As We May Think", the famous 1945 article by Vannevar Bush anticipating hypertext
Hypertext Publishing and the Evolution of Knowledge, a paper K. Eric Drexler
Review on Hypermedia Issues And Applications by V. Balasubramanian
Project Xanadu, the original vision by Ted Nelson (who coined the word "hypertext") of a universal hypertext network
Eastgate Systems Home Page: a firm distributing hypertext software and hypertextual novels
HyTime: an SGML language for hypertext, more sophisticated than HTML
Adaptive Hypertext Home Page
Adaptive Hypertext Project at NASA Ames
The Hyper-G Project: developing a more powerful distributed hypermedia network than WWW, see also: Hyper-G W3 Entry Point (IAESTE Information Server)
Hypertext links
-Computer Interaction, including Hypertext and Computer-Supported Cooperative Work
Hyper-G gateway to the Human-Computer Interaction Bibliography project with lots of papers and books
UK Virtual Reality Special Interest Group
Virtual Worlds archive
Project on People, Computers, and Design, headed by Terry Winograd
"Oz project" on generating virtual drama with real and computer-generated agents
Towards an Astrophysical Cyberspace:The Evolution of User Interfaces (hypertext paper)
Paramind and Para-literature
The Similarities Engine: recommends similar records based on your musical selection
Knowledge media: a rich collection of links on media to convey knowledge in a form so that they can be used to augment intelligence, including Information Retrieval, Design Patterns, Agoric Systems, Hypermedia, AI, etc.
CSCW Directory
Center for Computer-Mediated Communication
"Network Nation" revisited, a thesis on the present impact of Computer-Mediated Communication
Journal of Computer-Mediated Communication
Information Sources: the internet and Computer-Mediated Communication
Collaboration, Knowledge Representation and Automatability
WWW Collaboration Projects
World-Wide Web Project
Entering the World-Wide Web: A Guide to Cyberspace
World-Wide Web FAQ (Frequently Asked Questions) with the list of all available WWW-software
Challenges for a Webbed Society
Virtual Reality interface to the World-Wide Web (VRML)
Cyberspace: a paper on new protocols for a spatial interface to the Web
Project for an Intelligent Information Infrastructure
Project Metaphysics: Michael Heim's philosophical investigation of cyberspace and virtual reality
Autologue, a paper about self-organizing discussions on the Internet by Heath Michael Rezabek
LaTeX to HTML (WWW Markup Language) conversion
Automatic Visualization of Hypertext Webs
How to write HTML documents
Tips for WWW-information providers
enviroment for WWW publishing with structure and WYSIWYG editing
HTML Grinder
The Webhound WWW Interface
Intelligent Browsing Assistance for WWW
THE WEB DESIGNER
Yale C/AIM WWW Style Manual
CyberWeb: WWW Development
Information and Computation
Operations Research-LIBRARY
Linear Programming FAQ
College on Simulation Home Page
Evolutionary Psychology: A Primer, by Leda Cosmides & John Tooby
Society for Evolutionary Ethics, founded John David Garcia
Social and Cultural Evolution: a rich collection of on-line publications
Association for Politics and the Life Sciences
Philosophy in Cyberspace: an extensive guide to philosophy resources on the Internet
Liverpool University's guide to Philosophy resources
Stanford Encyclopedia of Philosophy: an expanding collection of texts on basic philosophical ideas
The Internet Encyclopedia of Philosophy, edited by James Fieser
University of Chicago Philosophy Project for the reading and discussion of texts
Center for Applied Ethics
services for philosophy
Electronic Journal of Analytic Philosophy
Tractatus Logico-Philosophicus(no longer available because of copyright reasons)
IPPE: Preprints of Philosophy Papers
ThinkNet: mailing lists and resources on Post-modern
philosophy, Systems Theory, Autopoiesis and Interdisciplinary studies
Onar Aam's series of essays on the origin of knowledge, from a cybernetic perspective
Ontology Research Lab at Stanford's CSLI, with a tutorial on the theory of abstract objects
Analysis
Origin Project: using the Internet to develop a universal philosophy / spiritual system, integrating insights from different religions and sciences
excellent FAQ
The Left Hemisphere: extensive list of links on Skepticism, Religion, and Secularism
The Institute: philosophical and scientific inquiry into
basic questions of human consciousness and existence, from cognition to quantum
mechanics
Fallacies of reasoning: an exhaustive listing
Foundation for the Future, created to study the long term evolution of humanity, towards the year 3000
Joël de Rosnay's "Crossroads to the future" page including a list of future-oriented web sites
Connect with the Future: extensive lists of future-oriented sites
Futures web sites: another list
Sasha Chislenko's home page with a list of Great Thinkers and Visionaries, and articles on future developments
Club of Rome , the famous international think tank reflecting on our global future
OECD Futures Programme
A Magna Carta for the Knowledge Age: Cyberspace and the American dream, a
"free market" view of the net, based on ideas from Toffler, Gilder, Dyson and others.
Cyberocracy" by D. Ronfeldt
Progress and its Sustainability
Trajectories, the Journal of Futurism & Heresy
FutureWeb: Future Studies program at University of Houston, provides a Futures Resources Index
Swedish Institute for Futures Studies
Millennium Project: a UN sponsored think tank for global and long-range forecasting.
World Future Society
Greater Boston Chapter of the World Future Society with many links on future-related web documents
Worldwatch institute
Resources for Futures Research
texts on Transhumanism: a philosophy that seeks to extend human capabilities to ever higher levels
Transhumanism, futurology and analytic philosophy: the Bostrom space
World Transhumanism Association, offering a Journal of Transhumanism
The Extropian Principles, the Extropy Institute and other information about extropianism, a "transhumanist" movement that shares many ideas with Principia Cybernetica, but puts more emphasis on free market mechanisms and technological applications for human expansion
Life-extension: plenty of links on ways of living longer
Better thinking with chemistry: an introduction and overview of intelligence enhancing drugs
Arcosanti: an experimental town demonstrating the possible integration of architecture with ecology ("arcology")
Foundation for Conscious Evolution: a network for raising conscioussness
Communications for a sustainable future: a progressive network for social and ecological issues
The Venus Project: aims to redesign culture for a sustainable future
New Civilization Network: a "New Age" style group working towards a better world
Foresight Institute: an organization formed to prepare society for
anticipated technologies, in particular nanotechnology, and Web Enhancement software./ul>
: hierarchically organized subjects with search possibilities
WWW virtual library: edited catalog of WWW info classified according to subject
EINet Galaxy: hierarchically organized subjects with search possibilities
Galaxy: hierarchically organized subjects with search possibilities
BUBL subject tree (based on library classification codes) from the BUBL information services
Joel's Hierarchical Subject Index is another attempt at organizing the knowledge available over the Internet
Globewide Network Academy wants to become a full university operating over the Internet, and already proposes a searchable Meta-Library of knowledge available over the Internet
One Look Dictionaries: search through some 50 web dictionaries at once, a most useful service!
Merriam-Webster Dictionary
Webster's Dictionary
Hackers' Dictionary
Technical and English Dictionaries at CERN
Dictionary of Computing terms
Dictionary of Cell Biology
Glossary of Mathematical Programming
list of on-line dictionaries (mostly translating, also more general)
WordNet is a lexical reference system containing some 100,000 English words, organized as a semantic network, with link types (including synonym, antonym, ISA, and HAS_PART) between words
Encyclopedia Britannica Online (pay service)
Encarta Online: search in an abridged version of Microsoft's encyclopedia
Interpedia project wants to build an encyclopedia distributed over the Internet (newsgroup comp.infosystems.interpedia); (seems defunct)
Global Encyclopedia, another volunteer attempt (seems defunct)
(Spider's Web) References
Net Guide Reference Shelf, with links to all kinds of lists, dictionaries, calendars, etc.
Usenet FAQs
Acronym search: find what all those abbreviations stand for
Lycos: extensive catalog
Infoseek: other extensive catalog
Alta Vista: other extensive catalog
Hotbot: extensive catalog
Open Text
Dogpile: search with different search engines at once
MetaCrawler: search with different search engines at once
Four11: Internet White Pages (find email addresses)
Netfind Search: finding E-mail Addresses
CUSI: a single form to
search a large number of different WWW search engines,
CUI collection of WebSearch Engines
Veronica: search Gopherspace
Global Network Academy MetaLibrary
JumpStation Search Page
Search Engines on Internet
Metasearch: a Lycos search to find more searchable indicesStanford Netnews Filtering Service: subscribe to a personalized selection of newsgroup messages
DejaNews: and Reference.Com: search all newsgroup messages
Directory of Scholarly Electronic Conferences: searchable list of mailing lists
Liszt: Search e-Mail Discussion Groups
Amazon Book: very large catalog
Internet BookShop (UK): very large catalog
Book Stacks-Search
Blackwell's Bookshop, Oxford
Powell's Books: very large catalog, with specialty store in the area of science
& technology
Moe's books: specialised in out of print or old books
Oxford Books, Atlanta
Computer Literacy Bookshop
Search intertain.com bookstore
Pages de France / recherche: for French books
List of Web BookshopsCARL UnCover: search a database containing millions of published papers in thousands of academic journals covering all disciplines. Selected papers can be faxed to you for a fee.
HYTELNET Libraries: telnet connections to all library catalogs on the Internet
It is possible to combine several keywords into boolean expressions using 'and', 'or', 'not' and brackets '( )' as logical connectives. E.g., all the above titles would be found by typing systems and theo. Another example: if you want to search for a document with the word 'cybernetics' in its title but NOT the words 'evolution' or 'theory', then enter the following expression in the search field:
Cybernetics and not (evolution or theory)
Searching on boolean expressions is much slower than searching on space separated strings, so use it sparingly.
Are Life and Meaning Coextensive?", in: Evolutionary Systems, ed. G. van de Vijvers, Kluwer Academic Publishers, in press.
Simulations of Evolving Embodied Semiosis: Emergent Semantics in Artificial Environments", In: Proceedings of the 1998 Conference on Virtual Worlds and Simulation 1998. Landauer C. and K.L. Bellman (Eds). The Society for Computer Simulation International, pp. 233-238.
| Synopsys: |
This is the web server of the Principia Cybernetica Project (PCP), an international organization. PCP tries to tackle age-old philosophical questions with the help of the most recent cybernetic theories and technologies. Stated more precisely, the Project's aim is the computer-supported collaborative development of an evolutionary-systemic philosophy.
To get started, there is an introduction with background and motivation, and an overview, summarizing the project as a whole.
As part of HyperNews, I've been collecting links to annotation mechanisms on the WWW.'
HyperNews to allow responses to any article.
Visit the Sudbury Neutrino Observatory!
Fitness as Default: the evolutionary basis of cognitive complexity reduction (draft paper F. Heylighen) (new)
HTML archive of PRNCYB-L messages, sorted according to topic, date and author
"The Ultimate Reality of Physics:
an essay in metaphysics", (FTP file) a paper by V. Turchin
"Selection of Organization at the Social Level", (FTP file) paper by F. Heylighen and Donald T. Campbell for the Special Issue of World Futures on "The Quantum of Evolution" (see also the issue's new Preface)
(extended summary of F. Heylighen's Ph.D. thesis, available as a book)
Heylighen & Bollen: Development and Publication of Systems Knowledge on the Internet: the Principia Cybernetica Web (paper on FTP, submitted to "Cybernetics and Systems") (new)
Memesis - the Future of Evolution)
Semantic Webs: A Cyberspatial Representational Form for Cybernetics (in PostScript, final paper for Symposium on Cyberspace)
:
Objective, subjective and intersubjective selectors of knowledge", Evolution and Cognition (to be published in the Spring issue devoted to D.T. Campbell's evolutionary epistemology)
Dynamic and adaptive structuring of the World Wide Web based on user navigation patterns". Proceedings of the Flexible Hypertext Workshop (ACM)
Cognitive Complexity vs. Connectivity: efficiency analyses of hypertext networks", in: F. Heylighen (ed.) The Evolution of Complexity (Kluwer, Dordrecht). [in press]
The next section gives the countries or domains ordered according to the percentage of consultation done by computers belonging to that domain. More detailed statistics (including all nodes and hostnames) can be found here.
Université Libre de Bruxelles (ULB) and the Dutch speaking Vrije Universiteit Brussel (VUB). The present web page provides a short overview of the combined "Free University", in the context of the Principia Cybernetica Web. For more detailed information, check the official VUB and ULB home pages.
The original Free University of Brussels was founded in 1834, as a reaction against the catholic domination in higher education (see the history of the ULB). Its name refers to the complete freedom of inquiry which is the founding principle of the university, and to the freedom of domination by either state or religious authorities. Like almost every institution in the bilingual Belgium, the Brussels university has been split up into a French and a Dutch-speaking part, which led to the creation of VUB as a separate institution in 1969 (see the history of the VUB).
Though ULB and VUB are now practically and legally independent, they maintain good contacts and continue to share their original philosophy which is liberal and progressive, based on the principles of free-thinking and humanism. At present, VUB has about 8000 students, ULB about 18000. Although registration fees for university studies in Belgium are already exceptionally low compared to other countries, the Free Universities have always done additional efforts to keep the costs of studying minimal, and to provide extensive social services and financial support, so that students from even the poorest backgrounds would be able to get a degree without discrimination.
Though in the social sense, VUB/ULB can certainly not be described as elitist, many of their researchers and research departments belong to the international elite. The ULB has many distinguished alumni, including Jules Bordet, Nobel Prize for Medicine in 1919, Albert Claude, Nobel Prize for Medicine in 1974, Ilya Prigogine, Nobel Prize for Chemistry in 1977, and Pierre Deligne, Fields Medal (the equivalent of the Nobel prize for Mathematics) in 1978. Especially Ilya Prigogine, one of the founders of the "Brussels School" in thermodynamics, has gotten world-wide fame for his discovery of dissipative structures, and the books ("Order out of Chaos", "From Being to Becoming", etc.) he has written, partly in collaboration with the ULB philosopher Isabelle Stengers. Although VUB is a smaller university with a much shorter history, it too has already produced several internationally famous scientists, including the philosopher Leo Apostel, who started his career at ULB under his equally well-known teacher Chaim Perelman, but became full professor at VUB, Jean Bourgain, Fields Medal in mathematics in 1994, Ingrid Daubechies (presently at Princeton), founder of the mathematical theory of wavelets, and Pattie Maes (now at MIT), a leading researcher in intelligent software agents.
For people interested in the cybernetics and systems domain, the most well-known research laboratories at the ULB may well be the Center for Non-Linear Phenomena and Complex Systems, founded by Prigogine, but now directed J-L. Deneubourg, and IRIDIA, the interdisciplinary AI institute, directed by Philippe Smets. The most interesting centers at the VUB may well be the AI-lab, headed by Luc Steels, and the transdisciplinary Center "Leo Apostel". There is more detailed info available on other departments and persons working at the VUB and at the ULB.
ULB and VUB share their Computing Center (BFUCC), which provides several services, including a gopher server, an anonymous ftp-server, a CRAY supercomputer and telnet to the VUB and ULB library systems. Moreover, there are many departmental servers: see the combined list of VUB-ULB Web servers.
Apart from its academic hospital and molecular biology unit, the VUB is mainly concentrated on one campus, "Oefenplein" at the Boulevard du Triomphe in the South-East of Brussels. The ULB has two main campuses, "Plaine" which borders the VUB campus "Oefenplein", and which houses the scientific faculties, and "Solbosch", about 10 min. walking from there at the Avenue Adolphe Buyl, which houses among other faculties the social and human sciences, and engineering. "Plaine" and "Oefenplein" together form a horseshoe-shaped region surrounded by large roads, with the ULB section in the rounded (South-East) part of the horseshoe (see the map in "how to reach the VUB").
In 1987, the VUB founded an English-language division, Vesalius College,
in association with Boston University. Vesalius College offers a US-style
liberal arts education and benefits from the increasing international
population in the larger Brussels area. In addition, both ULB and VUB offer numerous postgraduates (MSc, MBA, PhD, ...) in English.
Region of Brussels-Capital
Let's meet in Brussels
Brussels Tourist Information: lists of addresses and phone numbers
Brussels International City
How to get to Brussels
Brussels: the Rough Guide
Brussels in MS Expedia (with map)European Union, is the second international city in the world, as measured by the number of headquarters of international organizations. About a quarter of its 1 million of inhabitants consists of foreigners, most of which are either Arabic immigrants or civil servants, businessmen and diplomats working for the European Commission, NATO, or one of the many other multinational institutions or firms that are located there. The city is officially bilingual (all official announcements and street names are in French and in Dutch), but almost everybody understands and speaks English, and you will hear many more different languages when strolling through the city center. With its more than 1000 years of history the city offers many fascinating sights to visit. It boasts the most beautiful historic market square and the highest concentration of restaurants in the world.
The "Petite Rue des Bouchers" (street of the butchers) in the medieval center of Brussels is famous for the fact that every house in the street is a restaurant. The street is closed for traffic (anyway it is too narrow to let cars pass), and this allows the restaurants to exhibit some of their products (especially sea-food and fish) in a rather spectacular fashion in front of the passers-by. In some of the wider parts of the street it is also possible to eat and drink outside, watching the crowd strolling between the quaint, narrow houses.
The "Rue des Bouchers" is just a few minutes walking from the Grand' Place, the central market square of Brussels, which is said to be the most beautiful in the world. The square is dominated by the magnificent 15th century Town Hall, with its hundreds of little statues. Unfortunately, the most beautiful part of the Town Hall, the elegant tower, is hidden behind scaffolding, waiting for a much needed renovation. Even with the Town Hall in bad shape, the splendid 17th century buildings, with their golden inlays, surrounding the square, will certainly enchant you.
Not far from that magnificent Grand'Place in the medieval center, you can also find the tourist attractions of Manneken Pis (a not very impressive but quite funny statue of a pissing boy) and the cathedral of Saint Michel, part of which is being renovated. Other interesting places to visit include the Atomium, the imposing Palais de Justice, and for the nature lovers the many parcs, especially the splendid Bois de la Cambre, which is not far from the university, and the beautiful forest to which it once belonged: the Forêt de Soignes, with its centuries-old beech trees. The border of the forest, near the abbey of Rouge Cloître, is at walking distance from the Hermann-Debroux metro terminal.
The Atomium, an enormous steel construction representing an iron atom with 9 spheres connected by corridors, is situated in the parc of the Heysel, north-west from the center, which can be reached directly by metro. Here you will also find the Bruparck amusement park, which offers among other things Mini-Europe, a permanent outdoor exhibition of small scale (1/25) precision-made replicas of Europe's most famous architectural sights, such as the British Houses of Parliament, the Brussels Grand' Place, the Palace of the Dogues in Venice, the Greek Parthenon, and multiple others.
It is possible to visit the some of the buildings in the area around the Schumann crossing which houses the European Parliament, Council of Ministers, European Commission (the "government" of the European Community) and its administration.
Brussels offers numerous musea. Special mention deserve the (integrated) Royal Musea of Ancient and Modern Art (with a special section on the well-known Belgian surrealist Magritte), the museum of natural history with its collection of dinosaur skeletons, the museum of Art and History, near the impressive Cinquantenaire arc, Autoworld, which boasts the largest collection of old and new cars in the world, and the Museum of Comic Strips.
The most characteristic feature of Brussels is perhaps the rather anarchistically distributed architecture, sometimes splendid, sometimes ugly, but never boring, with medieval houses next to futuristic constructions, and with different houses of different heights, widths and styles, fraternally the one next to the other in any street. The most well-known style is the Art Nouveau, represented especially by the famous architect Victor Horta. The city can be roughly divided into the "High Town" (the south-east part), which is the richest with many splendid villa's and parcs, and the "Low Town" (the zone around the canal), where the buildings are often in a rather bad shape, but which contains the oldest and most picturesque parts of town. The best way to appreciate all this is just to walk or drive around in any quarter of the town.
Clickable Map: Belgium with major cities and borders of provinces (not up-to-date for the central province of Brabant)
Belgium is a small, highly developed and densely populated country (10 million of inhabitants) at the cross-roads of Western Europe. Belgium is one of the founding members of the European Community, and its capital, Brussels, is also the capital of the European Union. It is since recently a federal state, with 3 relatively autonomous regions: Flanders in the north, where the language is Dutch ("Flemish"), Wallonia in the south, where the language is French (although there still exists a not officially recognized "Walloon language"), and the centrally located Brussels, which is officially bilingual. Belgium's rich history has left impressive churches, town halls, castles and works of art, dating back to the early Middle Ages, spread around the cities and country-side.
Belgium has possibly the highest "quality of life" in the world, as testified by its excellent food, housing, health care, education and infrastructure, its world records for high productivity and low poverty, and the appreciation of foreigners residing in Belgium. For a personal view on what distinguishes Belgium and the Belgian character (good living, pragmatism, food and drink, open-mindedness, compromise, privacy ...), check my "Essay on Belgian Culture".
The governing of the country is very much complicated by the particular structure with three language communities (Flanders in the North, Wallonia in the South, and a tiny German speaking region in the East), and the multilingual, multicultural and multinational status of Brussels. The language in Wallonia is French. The language in Flanders is Flemish, which is officially the same language as the Dutch which is spoken in Holland. In practice, the differences between Flemish and Dutch (mostly pronunciation, also vocabulary and expressions) are comparable to the differences between British and American English, and are just big enough so that Dutch TV sometimes add subtitles to Flemish spoken movies. Although Brussels is surrounded by Flemish territory, the majority there speaks French. Flanders comprises about 55% of the 10 million of Belgian inhabitants, Brussels 10 % and Wallonia the remaining 35%.
There have been a lot of political conflicts between the two main linguistic communities, but the language problem, which is the issue that has received most publicity outside Belgium, is (at least in my view) much less important than it seems. Since the federalization of the state the linguistic conflicts seem to have very much diminished, now that politicians are no longer capable to blame difficulties on the "other side". There have never been any real conflicts between Belgian (Walloon and Flemish) people, as opposed to conflicts between Belgian politicians. The best illustration of that is that even during the most heated episodes, no one has ever been killed or seriously injured in clashes connected with the linguistic conflict. It suffices to consider similar situations in other countries where conflicts exist between cultural or linguistic communities (e.g. Yugoslavia, Canada, Northern Ireland) to conclude that such peacefulness is not the common rule.
Belgium has, since the Middle Ages, always been one of the richest and most developed regions in the world (just look at the historic churches, town halls, and pieces of art, in cities such as Brussels, Ghent, Bruges, and Antwerp to get an idea of the wealth during that period). This wealth was not due to natural resources, which are almost absent, but to trade, which was facilitated by Belgium's central position in Western Europe, and the presence of many land- and waterways.
Although it is fashionable in some quarters to view Belgium as an "artificial state", put together by the European powers after Napoleon's defeat, history shows that the region which is now called Belgium has been almost continuously under a single rule since at least the 16th century, when it got split off from Holland during the reformation. Before that period (and for a few years after the defeat of Napoleon), Belgium and the Netherlands were united, forming the "Low Countries", a remainder of the 3rd, central part of the Frankish empire, Lotharingia, in between France and Germany. There has historically never been a clear split between the Walloon and Flemish provinces. Insofar that there was a division in counties and duchies (Flanders, Brabant, Liège/Limburg, ...), the divide was East-West rather than North-South as it is now. (this is clearly seen on a set of historical maps of the wider German region). The "Flemish" painters and polyphonists who were famous throughout Europe in the Middle Ages and Renaissance often were of Walloon origin.
This lack of pride also leads to the lack of a clear image for the country abroad. Other comparable small countries have easily recognizable images: for example, Switzerland is immediately associated with banking, clocks and mountains, Holland with tulips, cheese and wind-mills. For Belgium, on the other hand, no clear associations spring to mind. This is due partly to the lack of image-building and marketing, partly to the fact that the Belgian culture and landscape is extremely varied, and cannot be summarized in a few symbols.
To my opinion, it is not due to the lack of a national identity, though. That national character is rather subtle, and not easy to formulate in a few words. Though Flemish and Walloon cultures differ in several respects (as could be expected, the Flemish are closer to the more disciplined Germanic culture, and the Walloon to the more loquacious Latin culture), they have more things in common than most are willing to admit. A clear sign of that is that though on the basis of language, Wallonia seems to fit in with the neighbouring France, and Flanders with the neighbouring Holland, no one in either Flanders or Wallonia has ever dared to suggest that their region should leave Belgium and join the more powerful neighbour state. Not even the German-speaking part, which was annexed after the first world war, is willing to rejoin the wealthy unified Germany.
What all Belgians have in common is a love for the "good life", which they find in their excellent food and drink, comfortable housing, reliable medical and social services, highly developed traffic and communications infrastructure. Belgians are not the type wanting to impress other people with their achievements, or to convince others of their righteousness. They tend to be rather reserved or introverted in their first contacts with other people, but are sincerely warm and friendly once you get to know them better. They are happy when they can enjoy a safe and comfortable life, together with their family and friends, and they put a high value on privacy. They have a clear aversion towards moralizing, towards telling other people how they should or should not behave (an attitude for which they critize their neighbours in Holland), and they take "live and and let live" as the basis for their philosophy. R. Hill, in a book on different European characters, describes the Belgians as "open-minded opportunists", noting their pragmatical attitude.
An anecdote illustrating this attitude was reported by a British officer commanding Belgian troops during the first world war. Whereas soldiers normally are supposed to follow orders without questioning, the Belgians would first ask why they were supposed to do something particular. Only after they got an acceptable reason they would execute the order.
Another character trait noted by Hill is a "democratic" attitude, in the sense that Belgians make very little distinction between classes or social strata. It is not because you are a professor, a noble man or a rich banker that you will be treated with special respect or privileges. Everybody has the right to be taken serious, and to get a good education and a decent way of living. On the economic plane, this egalitarian philosophy is illustrated by the fact that Belgium has the lowest percentage of poor people in the world.
Belgian workers are the most productive in the world. According to recent German statistics (1992), industrial productivity (amount of goods produced per worker) in Belgium is some 20 % higher than in the next most productive country, the neighbouring Holland, and well above that of the industrial giants Japan, Germany and USA. This is due to extended automatization, highly skilled labor, shift work that minimizes idle time, and low absenteeism. Although workers have relatively much vacation and free time, and can easily take time off for illness without risking to lose their jobs, few working days are actually lost. This is probably due to the excellent system of low cost medicine and the tradition of solving industrial conflicts by negotiations. Somewhat surprisingly, given the well publicized strikes, industrial unrest over the last 10 years in Belgium is one of the lowest in the European Union.
Thanks to the open market, the good distribution channels and the strong consumer requirements, one can find the most diverse and high quality goods in the shops at relatively low prices. The high production and consumption standards have led to the publicity slogan "This is Belgian" being used as a quality label (and not, as one might imagine, as an appeal to nationalistic feelings, such as "Buy American"). The association of "Belgian" with "high quality" is slowly diffusing to neighbouring countries, especially in the domains of food, drink and housing. More unexpectedly, Belgians (the "Antwerp Six" group) have recently made inroads in top ten fashion design, a domain which was almost exclusively under the control of French, Italian and Japanese designers.
All this, together with the generally peaceful atmosphere (the crime rate in Belgium is still one of the lowest in Europe), and the effort put into developing the basic things in life (Belgium is one of the few countries where there is no housing problem, because almost every Belgian family tends to build its own home) would put Belgium very high on a hypothetical "quality of life" ordering of countries. In international polls, Belgians always tend to come out among those most satisfied with their life and least inclined to emigrate to another country. This is in sharp contrast, but not in contradiction, with the very critical attitude which Belgians exhibit towards their country and government. (one can only conclude that they would be even more critical when living in another country).
The things that are especially noticed by foreign visitors are the excellent food, and the very dense concentration of restaurants and pubs, everywhere in the country (another world record). Belgian cuisine, which is related to the French one, offers many dishes worth trying. Especially the beer (see Patrick's Belgium Home Page) is a national speciality: there are hundreds of different types with distinctive tastes, which are all served in their own specially made glasses. It is a pity that the international marketing is not better developed, because everybody knows Dutch, Danish or German beers, whereas the Belgian ones (which are much richer in variety and taste) are known only by the real beer lovers. A better known speciality are the Belgian chocolates which are sold all over the world. And then there is the national dish, "French" fries ("frites"), which, according to legend, were invented in Belgium, not France, and which are supposed to be better here than in any other place in world.
In order to relativize this quite rosy picture of Belgium, let me also mention the most serious problems that are to be solved. There is first the large budget deficit (which after many economies is getting under control). This has led to a government debt, which, as a percentage of GNP, is the highest one in the industrialized world (OECD countries). The Belgian state as a whole has no external debt, though (in contrast to for example the U.S.A). This can be explained by the fact that Belgium has one of the highest savings percentages in the world. The debts of the government are more than compensated for by the credits accumulated by Belgian companies and households, which are eager to invest their money in government bonds, as they offer a high and reliable interest. The balance of payments for Belgium has been consistently positive for the last decennia. This may in part explain the ease with which the government has been relying on borrowed money.
Other problems are the continuing high percentage of unemployment, though the unemployed are still rather well protected by social benefits. Recently there have been troubles with the many Islamic immigrants, for whom it is difficult to integrate the Western culture and system, and this, more frighteningly, reinforces the popularity of extreme right parties.
king has no real power, and the prime minister is mainly the person who is best suited for implementing the agreements). For example, socio-economical problems are mostly avoided by preparing "collective labor agreements", where trade unions and employers reach a compromise on wage increases in the coming period. Only when unions and employers cannot reach consensus, the governement will intervene by proposing a compromise.A special expression, "a Belgian compromise", has been invented to design the typical solutions derived in this way: complex issues are settled by conceding something to every party concerned, through an agreement that is usually so complicated that nobody completely understands all its implications. In spite of the apparent inefficiency of these settlements, the compromises do work in practice, because they stop the existing conflicts, and thus allow life to go on without fights or obstructions. The practical ambiguities and confusions that arise out of the compromise are usually solved on the spot by the Belgians' talent for improvisation.
The experience gained in negotiating these intricate multiparty, multilingual and multicultural problems has led to an unlikely new export product: Belgian political expertise. At a certain moment, the presidents of the four largest political groups in the European Parliament, socialists, christian democrats, liberals and rainbow, were all Belgian, as is the president of the European federation of trade unions. The Belgian prime minister, Jean-Luc Dehaene, has recently succeeded in untying the Gordian knot of assigning some dozen different European institutions to the different member states of the European Union (a problem which had eluded the previous British and Danish presidencies of the European Community) by on the spot creating a new institution, so that every country could carry something home. This made him the front-runner in the race for becoming the new president of the European Commission (the "head of government" on the European level). (the only reason he did not get it was because of an unclearly motivated veto by Britain).
Another example of this peculiar way of problem-solving, which reached the international newspapers, was the royal question. All laws accepted by Belgian parliament must be signed by the king before they can be applied. Normally this is an automatic procedure, but in the case of the law legalizing abortion, the former king Baudoin, on religious grounds, concluded that his conscience did not allow him to approve the law. The government discovered a small paragraph in the constitution stating that approval of the king is not needed in situations where the king is incapable to govern, a provision for exceptional circumstances such as mental illness of the ruler. The compromise reached between government and king, was that the king was declared incapable to rule for just one day, enough to pass the law without his signature!
Though people who highly respect formal rules might be shocked by such a pragmatic treatment of a sensitive issue, the problem was solved in a for everybody acceptable way: the king's conscience was kept intact, and the democratic decision was implemented with a minimum of delay. For the future, a change of the constitution is planned in order to avoid similar problems.
One of the core ideas of the Principia Cybernetica ethics is that "cybernetic" immortality is an essential long-term goal we (or evolution) should strive for. However, when asssuming that immortality is "good" in an evolutionary sense, we must justify why we are not immortal as yet, being the products of evolution.
A useful way to look at this problem is Dawkins's "Selfish Gene"
picture of evolution, where the fundamental unit to be maintained by natural
selection is not the individual, nor the group or the species, but the
gene. Individuals are merely disposable vehicles for the replicating information
contained in the genes. As long as the genes survive (that is, are replicated
in offspring before the individual dies), the survival or death of the
individual is not very important. This leads to the "disposable soma" (disposable body) theory of aging, which we will summarize below.
Though some theories assume that aging (and hence death) are preprogrammed in the genes, thus implying some kind of evolutionary necessity of individual mortality, more recent theories explain aging without such special assumptions. The main idea is that every evolutionary adaptation has a cost: using genes for one specific activity or function implies that resources (matter, energy, time, neguentropy) are wasted, which thus can no longer be invested in another function. In practice there is always a trade-off, and it is impossible to simultaneously maximize two different functions (e.g. reproduction and survival).
For a gene, the main criterion that must be fulfilled or maximized in order to be naturally selected, is that its vehicle (individual organism) should survive long enough to be able to produce (numerous) offspring. Now, one might argue that the longer the organism lives, the more offspring it can produce, and the more copies of its genes will be made. Hence, the genes of organisms that do not age, and thus live longer, would be naturally selected. However, mortality depends on at least two different factors: (internal) aging, and (external) perturbations (accidents, diseases, predation, starvation, ...). Though a gene can make its vehicle or carrier stronger, smarter and more resistent, it can never completely eliminate all possible perturbations causing death.
On the other hand, we might imagine genes stopping the process of aging. There are enough examples of self-repair mechanisms in cells and organisms to suggest that this is possible. Moreover, the fact that genes themselves are immortal should be sufficient to counter any arguments based on uncontrollable deterioration because of the second law of thermodynamics. Indeed, it is well-known that primitive organisms (e.g. bacteria, algae, protozoids, ...) are in a sense immortal. That is, when they reproduce (by mere splitting of cells) there is no difference between "parent" and "offspring": both splitted cells continue to survive, and undergo further splits, without any apparent aging or senescence. Our own process of reproduction (meiosis) is merely a more complicated version of this, in which just a few cells (sex-cells or germ-line cells) can indefinitely reproduce, while the other cells die after a while. Even the increase of thermodynamic entropy can be counteracted indefinitely in an open system with a constant input of neguentropy. So there is no a priori reason why living systems would not be able to indefinitely maintain and repair their structural organization.
But the question is whether it is worthwhile for a gene to invest lots of resources in counteracting the effects of aging. The factor of death because of external perturbations could be measured as some kind of average probability for an individual to be killed in a given lapse of time due to external causes. This would make it possible to compute an average life expectancy, not taking into account internal aging. The normal life expectancy for primitive people living in a natural environment (unlike our own highly protective environment) seems to be about 20-30 years.
Now, if you are likely to die around the age of 25 by external causes, there is little advantage in spending a lot of resources on combating the effects of aging, so that you might theoretically live for 1000 years. That is why we might expect that in the trade-off between early reproduction and long-time survival the genes would tend towards the former pole, making sure that sufficient off-spring is generated by the age of 25, rather than trying to extend the maximal age beyond 120 years (the apparent maximum for humans).
This implies that if our present environment, where the probability of being killed by predators, starvation or diseases before reaching old age is much smaller than in the original human environment, would continue to exist for a million year or so, natural selection would promote genes that would make us live longer. (when we are speaking about an evolution towards cybernetic immortality, however, we mean a quite different phenomenon, on a much shorter time scale. This evolution would take place on the level of memes rather than genes. ) In fact, a similar evolution has been artificially produced in fruit flies: by only allowing the fruit flies to reproduce at an advanced age, there was a selection for longevity instead of a selection for quick reproduction. Thus, in a few years, time researchers were able to double the (very short) life span of the flies. This is an experimental confirmation of the disposable soma theory.
In conclusions, such genetic theories of aging seem to imply that death is not necessary for evolution: it is only a side-effect of the fact that a gene can spread more quickly by early reproduction than by long-term survival of its carrier, depending on the average life-expectancy (and reproduction expectancy) in the given environment. From the point of view of the selfish gene, there is no reason whatsoever why it should destroy older copies of itself in order "to make room for the newer ones" (a quote from our Cybernetic Manifesto). This is merely an anthropomorphization of "Nature" as an intelligent agent, looking ahead and concluding that the new generation should be promoted at the expense of the older generation. All genes are selfishly striving for survival, and the only thing that would make one of them give up the fight is because it is less fit than its rivals, not because it is "older".
From that point of view, I would even reject the more careful formulation that mortality "may be useful for genetic evolution". The only reason for mortality would be that not having it (i.e. maintaining the necessary apparatus for unlimited self-repair of cells and organisms) would take away many resources from reproduction, for a very small return in terms of reproductive fitness. But I would hardly call that "being useful".
life-extension) is to combat free
radicals by antioxydant chemicals such as selenium, Vitamin C and Vitamin E, or to
minimize their production by calorie restriction diets.
Another one is an apparently inbuilt limit on the number of times a
cell can divide (mitosis). This so-called Hayflick limit (of the order of 50 divisions) is
well beyond the one that is reached during normal life, and should thus
not be interpreted as a preprogrammed death. The hypothesis is that it
functions to limit the risks for the development of cancer or tumors (characterized
by unrestricted reproduction of cancerous cells). The mechanism seems to
be that during each splitting of a cell, the chromosomes are copied incompletely,
with a small stretch of DNA on the outer extremum being cut off during
the split. The outer stretches of DNA (telomeres) for a young cell are not functional,
so that losing them does not impair function. But after a sufficient number
of divisions, the process would start to cut off functional DNA, thus making
it impossible for the cell to survive. The cutting off does not happen
during cell divisions (meiosis) producing sex cells (sperm or egg cells).
Otherwise each subsequent generation would have less DNA than the previous
one. This reminds us of the fact that the loss of DNA is not an unavoidable
effect of increase of entropy or a similar physical principle leading to
aging.
Very recently, researchers have managed to synthetically produce the enzyme telomerase, which is capable of produce new telomeres. This open up new avenues to combat those forms of again linked to the Hayflick limit.
See Further:
Theories of Aging FAQ
Theories and Causes of Aging from the Aeiveos Science Group
Evolution and ageing. Genome, 31: 398 - 405, a paper
Medline references for Aging Reviews
The Aging Research Centre
Aging: a quick review of theories
Life Extension by Brian Delaney
articles on aging in the Chicago Tribune
