Definition of Fitness in terms of transition probabilities

"Fitness", the hypothesized quality distinguishing systems or states that are selected from those that are eliminated, can be reformulated as a general measure F for the likeliness that a particular configuration x will be reached in a stochastic process:

F (x_i) = Sum_j P(x_j -> x_i) (i,j {1,...,n}, )

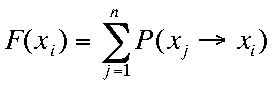
where P(x_j -> x_i) is the probability of the transition x_j -> x_i

High fitness (F > 1) of a state x means that on average more transitions enter x than leave x (the sum of all transition probabilities leaving x can never be >1). Thus, while the process runs, high fitness states will become more probable, and low fitness states less probable, as would be expected from a process undergoing natural selection.

A doubly stochastic process is defined by the requirement that F (x_i) = 1 for all states x_i. It can be shown that double stochasticity is a necessary and sufficient condition for a Markov process to be characterized by a non-decreasing statistical entropy function, i.e. a function of the probabilities which can only increase (or remain the same) over time, whatever the initial distribution of probabilities. Such processes correspond to the irreversible processes implied by the second law of thermodynamics. In a more general process, fitness can be larger or smaller for different states, and thus probability would tend to concentrate in the high fitness states, decreasing overall entropy. So, a necessary and sufficient condition for a Markov process to allow self-organization (i.e. decrease of statistical entropy) is that it have a non-trivial fitness function, i.e. there are x's such that F(x) =/ 1. Assuming classical probabilities, the sum of all P's must be 1 and thus we have the condition: Sum_i F(x_i) = n. Therefore, for every F(x) > 1, there must be at least one F(y) <1. This condition is equivalent to saying that selection is possible, because there are different fitness configurations from which to choose.

Having symmetric transition probabilities is a sufficient condition for a Markov process to be doubly stochastic. Indeed, symmetry means that P(x_j -> x_i) = P(x_i -> x_j) for all i,j and thus: 1 = Sum_j P(x_i -> x_j) = Sum_j P(x_j -> x_i) = F(x_i).

Therefore, having asymmetric transition probabilities is a necessary condition for a Markov process to have non-trivial fitness, and thus, to allow self-organization.

We can also interpret the P's not as probabilities but as effective numbers or frequencies N (e.g. size of a population) which can be different from 1. In that case, the total number N = Sum_i N(x_i) can increase or decrease during the process, and we get a model that resembles population dynamics, where fitness gets its traditional meaning from biological evolution theory: F (x) = N(x(t)) / N(x(t-1)).