Heylighen F. (1990): "A Structural Language for the Foundations of Physics", International Journal of General Systems 18, p. 93-112.
CLEA, Free University of Brussels, Pleinlaan 2, B-1050 Brussels, Belgium
It is argued that the difficulties to establish foundations for a unified physical theory are due to the predicative structure of the traditional scientific languages, whose descriptions reduce all phenomena to static, independent elements. A new language is therefore proposed, whose descriptions are fundamentally dynamic and holistic. It is based on the concept of "arrow": a relational entity which is completely determined in a bootstrapping way by the other arrows it is connected with, so that it has no independent meaning. An arrow represents an elementary process, and connected assemblies of arrows represent physical structures. It is shown how the fundamentals of space-time geometry can be expressed in this extremely simple, "structural" language. It is argued that this description could be extended to the observation process, and thus to the fundamentals of quantum mechanics, by introducing cognitive structures.
INDEX TERMS: language, structure, physics, holistic, dynamic, space-time, relations, bootstrapping, cognition.
With the renewed interest in the foundations of physics, it has become clear that the problems encountered in this domain are more than just questions of choosing an appropriate "philosophy" or "interpretation" concerning the fundamental theories. The traditional approach advocated a pragmatic viewpoint, which consisted in using the established formalism to get numerical values which could be corroborated with experiment. The deeper understanding of the formalism was considered a minor problem to be left to "philosophers", or was even, according to the Copenhagen school, abandoned completely. The fundamental problems, however, subsisted in spite of the many decades of efforts performed by some of the more philosophically inclined physicists. These problems, which are most clearly exhibited by the so-called paradoxes of quantum mechanics, have become even more urgent after some recent experiments,[1],2 which confirmed the paradoxical predictions. On the theoretical level, old problems such as the quantization of general relativity or the existence of divergences in quantum field theory, still seem impossible to solve in a satisfactory manner. The only evolution seems to be that fundamental theories are still getting more complex, producing ever increasing lists of "elementary particles" and "fundamental constants'. This is in sharp contrast with the belief that the more we approach the fundamental level of physical reality, the simpler things will become. Advocating a pragmatic viewpoint is no longer acceptable as a means for evading the crisis, unless one believes that there is a clear pragmatic utility in building ever bigger machines and making ever more complex calculations in order to get ever more numerical data about phenomena whose practical function, real nature or even very existence remains completely vague.
In fact it probably is just this pragmatic philosophy which is responsible for the
fact that so relatively little progress has been made in the fundamental theories of physics since the creation -- half a century ago -- of relativistic quantum theory. The root of the problem may well lie in the orthodox methodology of Bohr, who insisted on the basic (correspondence) principle that any (microphysical) phenomenon should be interpreted through the classical language of macroscopical observation, even though one knew this classical description to be inadequate.[3] The resulting problems of incompleteness and paradoxicality were met by the strange idea of "complementarity" which states that since it is impossible to give a complete description of an elementary phenomenon in classical terms, one should be content with giving different partial descriptions which, when taken together, would provide a kind of complete view, even though they are mutually incompatible. It is clear that such a viewpoint precludes any tentative to really understand what happens on the fundamental level. What I want to argue here is that the problem of partial and incompatible descriptions is not inherent in the elementary phenomena, but in the language we use to talk about them. This problem is not only a problem of incompatibility of different terms within the same theory (such as "position" and "momentum" in quantum mechanics), but even more a problem of incompatibility of different theories or languages which speak about the same physical reality (e.g. the quantum of Hilbert space language, and the relativistic or space-time language).
These specialised languages of physics are in fact modelled after the everyday, verbal language. This means that their structure consists of subjects (these represent physical objects or systems, such as a particle or a planet), to which different predicates (physical properties, such as position, spin, mass...) are attributed, following the rules of syntax, which specify which combinations are allowed, and the rules of the internal logic, which specify which combinations are necessary. Although this subject-predicate scheme may be useful for ordinary conversation, it is not very well suited for analyzing the profound structure of physical reality. This structure is indeed fundamentally holistic and dynamic, while the elements of description (subjects and predicates) are mutually independent, static units, each carrying a distinct and not further analyzable meaning. Using a subject-predicate scheme for description is equivalent to cutting the basically coherent and evolving world into static pieces. Of course there are many different ways to cut something in pieces, and one cutting method will in general exclude another one. This accounts for the fact that so many incompatible descriptions coexist.
This intrinsic limitation of the subject-predicate scheme has partially been met by the elaboration of ever more sophisticated mathematical formalisms. These have succeeded in making the structural-holistic and dynamical aspects of the world more explicit, while reducing the importance of the chosen units of description. Their framework, however, is still based on set theory, which is formally isomorphic to predicate logic, with "elements" as equivalents for "subjects", and "sets" as equivalents for "predicates". Structure and dynamics are added to the basic sets of descriptive units in a hierarchical manner. Traditionally this hierarchy consists of the following levels of description: (I) a subject, i.e. a physical system, such as an electron or a "material point", (2) a set of predicates, called states, coordinates or properties, which can be attributed to the subject, (3) a logical structure, specifying the logical relationships of implication and orthogonality between the predicates (classically this logic is implicit in the description by means of sets, but in quantum mechanics as projective structure is added, leading to what is called a "quantum logic", (4) a geometrical structure, specifying the topological and metrical relationships between certain "atomic" predicates. It usually takes the form of a manifold, (5) a dynamical structure, determining how, in the course of temporal evolution, actual predicates are to be replaced by other predicates, in accordance with the constraints provided by the logical and geometrical structures. This is usually expressed by a differential equation or a dynamical operator.
This hierarchical scheme is not absolute: in different theories you may find that certain levels were added, were eliminated or even have merged (for example the geometrical and dynamical levels in general relativity). The general evolution of physics, however, tends to increase the number of descriptive layers. New theories, indeed, tend to be built upon the skeleton of an existing theory, while trying to incorporate a novel structure. For example, quantum gravity is based on the framework of classical gravity, to which some of the descriptive levels of quantum mechanics are added.
It is no wonder then that present theories have become so complex, and are so far removed from their conceptual bases, that no one is left who has a clear intuition about the phenomena they describe. Starting anew seems to be the only way out of this problem. This means that a new basic level of description is to be uncovered. One of the most appealing expositions of this need for a new base may be found in Wheeler's concept of "pregeometry", which was urged by the problem of the incompatibility of the world pictures provided by quantum mechanics and general relativity.[4] The past decades have witnessed a number of attempts to construct such a new framework. These were inspired by such diverse methods, as logic of physical observation,[5],6 computation,[7],8,9 network theory,9,[10] quantum set theory,[11] discrete alternatives.[12]
Revolutionary as they are, none of these departures, however, is radical enough with respect to the language problem I have just sketched. In one way or another they all retain some part of the conventional subject -> predicates -> logic -> geometry -> dynamics hierarchy. This is shown most fundamentally by their starting from static, independent units of description, which are in this respect still isomorphic to subjects or predicates, even though they are called "propositions", "bits", "urs", "quantum sets", "spins" or "cells". From my point of view, the basic level of description should incorporate the dynamic and holistic features of the physical universe. Generalizing a remark of Finkelstein,9 I could say that the conventional hierarchy is, in this respect, upside-down. The fundamental level is to be found in the dynamics, in the idea of a physical process, which is something which, by definition, cannot be an independent unit, since it is always "in between" its beginning and its ending. Each process is the result of, and leads to other processes. In this way processes can be seen as forming an indivisible, dynamical pattern, a holistic structure, from which the geometrical structure of space-time is to be abstracted. The third level in this inverted hierarchy should be the logic, i.e. the description of recurring, invariant (i.e. independent of the localization in the geometrical framework) relationships between processes. Processes which are part of such invariant subpatterns may be labeled according to their functions. This leads to the fourth level: the predicates, which are labels for invariant functions or features. Finally, specific subpatterns which are characterized by certain predicates may be identified as subjects or physical systems.
To achieve such a program of rewriting physics, we need a simple and very general language which is able to express in a direct way this patterning of elementary processes, without presupposing something like a subject-predicate scheme. In the following pages I shall present a formal language which seems to meet these requirements. I shall then make a start with the rewriting task and show how the fundamentals of space-time structure can be expressed in it. Finally, I shall sketch some possible ways in which the following levels may be constructed.
If you want to describe a new language, you need another, already known language to speak about it: a metalanguage. For clarity and to facilitate the contact with conventional theories, I shall choose the traditional formal language of mathematics (mainly set theory and predicate logic) as metalanguage. To avoid any confusion it is necessary to keep in mind that there is an essential distinction between this metalanguage, which is based on the classical subject-predicate scheme, with independent units of description (the "words" of the language) and the object language, which is not. For example, when in the following I shall talk about "a set of arrows", it may appear that these "arrows" are just independent units, elements of a conventional set. The term "set of arrows", however, belongs to the set theoretical metalanguage, but represents a structure which is basically different from a set.
In order to make contact with the physical reality I try to describe, I shall introduce expressions from a third, informal language, whose terms denote known physical phenomena, which are possible interpretations of certain structures of the object language. In order to avoid confusion with the conventional usage of these expressions, which connotes a number of conventional theories, they will be written in italics. For example, when I call a certain structure of the structural language a "particle", this does not mean that it is equivalent to the concept of particle as it is used in traditional particle theories, but rather that it has a certain isomorphism with the physical phenomenon which is denoted by this concept. Whether this structure or the traditional concept will provide the best model for the phenomenon remains to be studied. In this stage, no fair comparison is possible, since the traditional description is still far more detailed, and has a better elaborated coupling with empirical reality. For the novel description the problem remains that beside the new language you also need a detailed translation from the old language into the new one. When the two languages are so basically different as in this case, such translation is a very demanding task.
As was argued before, for the fundamentals of the new language we need something which is intrinsically dynamic (i.e. it contains a notion of movement, of process) and relational or holistic (i.e. it cannot exist on its own, it loses all meaning when separated from its environment). Let us call such an entity an "arrow", and represent it with a bold letter a, b, d, ... The class of all arrows will be denoted by the Roman letter A = {a, b, d, ...}. The term "arrow" connotes an orientation. This stands for the dynamical aspect: there is a travelling, a movement in a certain direction; something is transmitted from the "beginning" to the "ending".
In order to express the holistic aspect, it must be possible to connect
these arrows together. This can be represented by introducing a connection
relation: C 
A x A.
a C b is to be read as "a is connected
to b". Since the arrows are oriented, this relation should
also be oriented, that is to say asymmetrical. We want to express that
every arrow is determined by its environment, consisting of the other arrows
it is connected with. Therefore we will define the "environment"
of an arrow as consisting out of two sets:
DEFINITION: define the input (I) and output (O) sets of an arrow a
A: I[a] = {d A|
d C a}, and O[a] = {d 
A|
a C d}.
We do not want arrows to be independent units, like the subjects and predicates, or elements and sets of conventional formal languages. We would rather like to express that arrows are determined relationally: they are only meaningful in relation to the other arrows they are connected with. An isolated arrow is intrinsically meaningless. This property can be represented formally by introducing the following "fundamental axiom" of the structural language.
AXIOM: each arrow is completely determined or defined by its input and
output sets: 
a, b A:
(I[a], O[a] ) = ( I[b], O[b] ) =>
a = b. In other words, a and
b are distinct if and only if their input and output sets are distinct.
This axiom expresses the fact that each arrow only "exists", that is to say, "can be distinguished as a separate unit", by its being connected to other arrows. This axiom can be interpreted as a typical example of a "bootstrapping" definition. Indeed, the axiom defines a in terms of I[a] and O[b]. However, I[a] and O[b] themselves are defined as sets of arrows, for example, I[a] = {s, d, e}. s is defined by I[s] and O[s], but I[s] itself contains a, that is to say the element we wanted to define in the first place. Hence, a is defined indirectly by itself!
It is interesting to compare such a "bootstrapping" definition with the more conventional "recursive" definition of an element. An example of a recursive definition would be: a is an arrow if it belongs to the input- or output set of an arrow; s is an arrow. In that case we would conclude that a is an arrow since s is one. Here it is necessary to state a priori that certain elements are primitive arrows. The other arrows can then be recursively generated from the set of primitive arrows. A recursive definition hence makes a fundamental distinction between "primitive" elements, which are independent, and elements determined by other elements. In a bootstrapping definition, on the other hand, there are no primitive elements: every element is (directly or indirectly) determined by the whole of all the elements.
A recursive definition can be interpreted as a procedure for checking whether a given element has a certain property (belongs to a certain set) or not. It has the property if it can be "reduced" to one of the primitive elements to which it is connected by a chain of recursive generations of elements. Hence, recursive definitions implicitly assume a "reduction-istic" philosophy. A non-reductionistic, bootstrapping definition can also be interpreted procedurally, by using it as a "double recursion". This means that the class of elements to be checked is split in two parts, say A1and A2. One part A1is considered primitive with respect to the other part, so that A2can be checked on the basis of A1. Then the situation is inverted and A1is checked on the basis of A2, which is now considered primitive. For example, the distinction between a and b can be checked by looking at the input and output sets, containing s. If these sets are the same, a and b are identified, otherwise they remain distinct. Then, on the basis of the new situation (a and b identified or not), the distinction between s and some other element can be checked, leading to a new situation. This distinguishing/identifying of elements can continue recursively, until no further identifications are possible, that is to say until it is certain that all remaining elements are distinct.
Such a bootstrapping procedure is often used in empirical domains where there are no obvious primitive concepts. For example, in psychology correlations between "personality traits", defined by tests, are studied in order to derive more adequate traits and tests. Since none of the traits one starts with can be considered primitive, one set A1of traits is used to refine another set A2, which then is used to refine the first set A1, and so on, until a more or less stable system of traits emerges. This is a practical example of "pulling oneself up by one's bootstraps": there is no stable ground (primitive elements) which can be used as a support from which to lift up (generate) other things.
A first corollary of the basic axiom is that arrows without any connection at all (that is to say with empty input and output sets) cannot be distinguished. In the limit there is only one such element: the "empty" arrow. This means that in practice all arrows must have some connections with other arrows in order to be meaningful. In the present framework, "meaningfulness", or even "existence", of arrows (in the sense that they can be recognized or labeled) is synonymous with "distinguishability". It can indeed be argued that the minimal requirement for a language to allow the transfer of "meaning" is that it propose a conventional set of distinctions20. In particular, each model or representation of a domain can be analysed as a distinction system 20, 21.
This provides a basis for discussing the semantics of the structural language. The analysis of a conventional language is based on the quadruple: lexicon (vocabulary), syntax (grammar), semantics (meaning of expressions) and pragmatics (practical use of the language). In the structural language lexicon and syntax are trivial: the lexicon is formed by the class of all arrows ("words"), but all arrows are equivalently meaningless, unless they have specific connections. The sentences or expressions of the language are formed by combining arrows into connected assemblies (networks or directed graphs), to be called "structures". Every combination of arrows forms a structure, so there are no syntactical rules needed to prohibit certain combinations. In fact everything which can be represented by drawing an oriented graph, is a structure. In this sense the structural language is rather graphical or pictorial than verbal (see23 for the practical use of graphical representations).
In order to interpret - i.e. to attach meaning to - a certain structure, it needs to be distinguished from other structures in an unambiguous way. In general, invariant distinctions within a network of connected arrows can be generated through the concept of "relational closure"22. "Closed" structures are characterized by certain mathematical properties, guaranteeing the invariance of distinctions22. (Remark that a distinction between structures, generated by closure, is determined recursively, in contrast with the distinctions between arrows, which are determined by the fundamental axiom in a bootstrapping way.) This is a general procedure for generating higher-order distinctions, that can be applied to any domain. In the present paper, however, we will only distinguish structures having an interpretation in the domain of the foundations of physics, without explicitly using the concept of "closure". This means that we will define some particular structures such that a correspondence ("homomorphism") can be established between on the one hand the formal properties of and relations between these structures, and, on the other hand, fundamental physical phenomena, such as space-time, causal precedence, and particles. This correspondence determines the semantics of the language.
In the present paper we will not discuss the pragmatics. In general, however, a language such as this, characterized by a network of connections and the generation of distinctions by closure, can be used in practice for the modelling and structuring of complex problem domains. In particular it can be used to reduce the complexity of a given representation22. It can also be implemented in the form of a computer support system23.
Let us conclude this section by discussing the relation between "arrows" and "connections". You may have remarked that arrows were introduced as elementary subjects, whereas the connection relation was defined as a predicate attributed to the arrows, apparently in contradiction with our objective of creating a language that is not based on a subject-predicate scheme. However, like stated in the beginning of this section, the structural language can only be defined by means of a subject-predicate type of metalanguage. The distinction between arrows and connections is purely artificial, forced upon us by the set-theoretic metalanguage. Let me clarify this by an analogy. In the language of classical physics an elementary physical system is either a "particle" or a "wave": it cannot be both. However, in the language of quantum mechanics (e.g., von Neumann's Hilbert space formalism), there is no distinction between particles and waves. If you insist on describing a quantum system in the classical language, you are confronted with Bohr's complementarity principle, stating that you are to describe the system in both ways (particle and wave), which are mutually exclusive, yet jointly necessary in order to exhaustively describe the system20,21. In the same sense, arrows and connections can be viewed as complementary descriptions of what is essentially the same entity.
It is always possible to switch from one description to another one. Indeed, each connection can be instantiated by an arrow: a C b can be rewritten as: there exists an arrow e1such that a C e1, e1 C b. (In the next section it will be shown that such an arrow e1belongs to a special type, to be called "event".) This procedure could be repeated indefinitely, and a new arrow e2might be introduced such that e1 C e2, e2 C b, after which we might again introduce an e3, and so on. In order to avoid possible ambiguities due to this freedom of definition, we shall in the following identify all arrows connected in a chain-like fashion, i.e. without bifurcations (input or output sets containing more than one arrow): O[a] = e1= I[e2], O[e2] = e3 = I[e4], etc., then put: e1= e2 = e3 = ... (This convention of identifying arrows connected in a sequence without bifurcations can be interpreted as a second axiom, which extends the relative indistinguishability determined by the fundamental axiom.)
In the same way as connections can be replaced by arrows, arrows can also be replaced by connections, but this only applies to special types of arrows ("events", to be defined in the next section). Yet every arrow, or sequence of connected arrows ("path"), can be interpreted in a generalized sense as a connection. This generalized connection relation simply corresponds to the transitive closure of the original connection relation.
Until now, the core of the structural language as I have exposed it, may have seemed so trivially simple that you may wonder whether anything really interesting can be expressed with it. The richness of the language lies, however, in the boundless variety of structures, each of which is only limited in its expressive power by its finiteness, by the way it is singled out, cut off from its environment. In principle, one should be able to model the entire dynamic universe with its elementary processes by using one giant arrow structure. The modelling of isolated phenomena could then be carried out by ignoring most parts of this universal graph, while retaining just those substructures which are at once necessary and sufficient to characterize the phenomenon in an ambiguous way. This is not an easy task. It presupposes the ability to analyze the concept we have of the phenomenon into conceptual units, which are not concepts themselves, which have no proper meaning but the one they get through their function in the whole. Since it is practically impossible to analyze something whose meaning always remains more or less vague and subjective in such a radical manner, I shall not follow this procedure in a consequent way. I shall partially work in the inverse direction, i.e. I shall start from a given simple structure and try to find a concept which matches it. An equilibrated combination of both procedures should provide us with a provisional collection of basic structures together with their approximate interpretation.
First I shall introduce two new relations which are derived from the fundamental connection relation:
DEFINITION a ib iff 
b A such that a I
[d] and b I [d] (a
and b are "input contiguous", they are connected to the
same arrow d).
Equivalently: a O b iff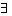 
b
A such that a O
[d] and b O [d] (a
and b are "output contiguous", they have the same arrow
d connected to them).
These relations are by construction symmetric and reflexive. Whereas the connection relation C emphasizes the sequential aspect of an arrow structure, i.e. the fact that different arrows follow each other, forming a sequence or a "path" (i.e. a linearly ordered set {d1, d2, , . . . , dn} of arrows such that diC di+1, (i = 1, ..., n-1), the two contiguity relations describe the parallel aspect, i.e. the fact that a given path can bifurcate, and that different paths can have the same origin or terminal point.
We are now able to identify a special class of arrows, namely those arrows which are not part of a bifurcation, i.e. which are not contiguous with any other arrow:
DEFINITION a A is an event iff a I
b or a O d implies b = a, d = a.
Since we have accepted to identify all arrows connected in a sequence without bifurcations, there cannot be two events connected to each other. Hence, any path joining two events must have at least one bifurcation.
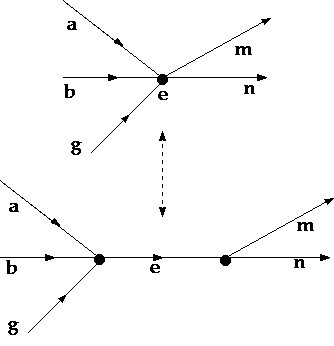
Figure 1: "reinterpretation" of a vertex e as an arrow e.
To get a better insight into the meaning of these "events", it is helpful to consider a graphical representation of a structure (Figure 1). The arrows will be represented by oriented arcs. When two arrows are connected, this will be represented by a vertex where the two arrows meet, but in such a way that one orientation is "ingoing", whereas the other one is "outgoing". Each vertex will thus have a number of ingoing arrows, forming an input set, and a number of outgoing arrows, forming its output set. According to the fundamental postulate, this means that the vertex (or the connection it represents) can be reinterpreted as an arrow, which is defined by its input and output sets. As is easily seen, such a "reinterpreted" vertex or connection will be characterized by the fact that it has no contiguous arrows. Equivalently, each arrow which has no contiguous arrows can in this way be represented by a vertex, or be reduced to a connection. These operations of reinterpretation of arrows and connections do not represent real transformations of the structural description. They only exist on the level of the metalanguage where they represent a change of perspective in the way of translating the structural expressions into set theoretic terms (cf.21). The only feature which is significant on the structural level is the fact whether a given arrow is, or is not, contiguous with another arrow. The arrows of the second category can be represented by vertices or connections, while those of the first category cannot.
If we go back to our provisional interpretation where arrows are viewed as elementary processes whose patterns resemble Feynman diagrams, it becomes clearer why the arrows of the second category, which are isomorphic to vertices, were called events. They can indeed be used to represent those phenomena where a number of processes or signals come together (input channel), react, and result in a (generally different) number of outgoing processes or signals (output channel). In the traditional terminology of physics such phenomena are called "events". Further characteristics of events will come to the foreground when space-time structures are introduced.
The following structure I want to introduce is a preorder relation on the set of arrows, which determines a kind of relative "length" or "duration".
DEFINITION a L b (a is longer than
b) iff there exists a path P={d1, d2,
..., dn} such that b P, d1O
a, dn I a. (Let us call such a path "parallel"
with a).
This means that there are two events e1 and e2 such that e1 C a, e1 C d1and a C e2, d1 C e2. So you can go from e1 to e2 by two different routes: either directly through the arrow a, or indirectly following the path P. Since e1 and e2 are interpreted as actual, physical events, the duration of an information transfer from e1 to e2 is fixed, independent of the route which was followed by the signal. Hence we can say that a and P have the same duration. Since b is a part of P it will have a duration which is shorter than that of P or a, and thus we have a L b. The definition of the duration relation can be extended in an evident way to incorporate paths instead of arrows. This relation provides a structural base for describing those features of the universe that are represented in the traditional framework by a topology or a metric.
A first application of the duration relation can be found by noting that there are no arrows which are shorter than events: e event, then e L a implies e = a. This follows directly from the definition.
On the other hand, any event e can be reinterpreted as
a connection between its input and output arrows. Suppose a
I [e] (the reasoning for a
O [e] is equivalent). Then we could say
that the path {a, e} is parallel with a, since it
has the same (reinterpreted) input and output arrows, and thus we have
a L e. In this sense, each event is shorter
than the arrows it is connected with. This accords with the intuition that
events are "instantaneous" phenomena, which have a minimal or
atomic duration.
DEFINITION (horismotic relation) 
a, b
events: a -> b iff there exists a unique path P={d1,
. . . , dn} such that a C d1, dn
C b (if a = b then put P = O). The arrows d1,
. . . , dn of P are called light signals (when they
are not events). This relation satisfies the criteria of Kronheimer
and Penrose[13] for a horismotic
relation: for any sequence of events {ai|i=1, ...,n} such
that aj -> aj+1(j=1,..., n-1) you
have that (i) ai-> an implies ah
-> ak (1=<h=<k=<) (ii) an
-> ai implies ah = ak.
This last property expresses the fact that the horismotic relation contains
no cycles or circuits: suppose you have a path P={d1,
. . . , dn} from a to b and a path P`={d1,
. . . , dk} in the inverse direction, so that the concatenation
P`o P forms a closed path or circuit. You can then construct
a new path from a to b by concatenating this circuit with
P: P o P` o P . This means that the path P
between a and b is not unique, and thus that a and
b are not related by the horismotic relation.
We can now apply one of the constructions used by Kronheimer and Penrose,13 and introduce two new relations:
DEFINITION a) (causal precedence) a, b events then
a < b iff there exists a path P={d1,
. . . , dn} such that i: di
is a light signal and a C d1, dn
C b.
b) (chronological precedence) a << b iff a < b and not a -> b.
We can now try to interpret these new structures by studying their properties. First we can remark that light signals are minimal with respect to the duration relation: there are no arrows shorter than light signals (except--in a special sense--events). This means that the processes represented by light signals are the "fastest possible", without being instantaneous as the events. If we go back to traditional physical theories we can choose to identify the "limit velocity" determined by these processes with the speed of light. The horismotic relation then determines the null light cone: "a -> b" means "b lies on the future null cone of a".
The causal and chronological precedence relations represent respectively the full light cone, and its inside. In the traditional language of relativity theory we can interpret "a << b " as "a and b are separated by a timelike interval", and "a < b " as "a and b are separated by a noon-spacelike interval". The three relations ->, < and << together with the set of events form what Kronheimer and Penrose call "a causal space",13 and which is a structure abstracted from the conventional manifold representation of relativistic space-time.
We have been able to insert the events and light signals in an abstract space time structure. We shall now try to interpret the remaining types of arrows within this same framework. Chronological precedence is a partial order relation which provides a time ordering between events. This ordering can be used to characterize the arrows which connect these events:
DEFINITION The arrow a is a particle iff its input and output events (e1, e2) are ordered by <<:
e1 C a, a C e2 then e1 << e2.
The rationale behind this choice of name is that the phenomenon which is conventionally called a (massive) particle, is an elementary process which propagates forward in time, inside the light cone. Remark that the definition of << excludes arrows with an orientation opposite to the chronological ordering (such arrrows would lead to light signal paths involving circuits, and this is prohibited).
It is however possible to introduce a less strict definition of chronological precedence which would extend the set of particles and allow antiparticles (i.e. processes moving backward in time, according to a "reinterpretation principle"[14] which was put forward, among others, by Feynman). Let us denote this extended chronological precedence by <<'.
DEFINITION e1, e2
events: e1<<e2 iff there exists
a linear path P = {d1, . . . , dn}
such that d1<<dn (suppose d1and
dn are events) and e1 C di,
dj C e2 with 1=<h=<k=<n (a
linear path is a path P without loops or circuits, i.e. dk,
diP: dk C
di implies i = k +1).
Such a chronologically ordered linear path can be interpreted as a world line, i.e. the trajectory of a signal moving inside the light cone. It is then reasonable to require that all the events on this world line, and not only the ones on the extremities, be temporally ordered. Any arrow belonging to such a path may be called a particle. An antiparticle can then be defined as an arrow a (input event e1, output event e2) whose direction is opposite to the <<' ordering: e2<<' e1(i.e. it is "antiparallel" with a particle or a linear path of particles). Remark that this definition allows the existence of arrows which are at the same time particle and antiparticle. Note also that this construction will produce more particles than antiparticles since for each antiparticle there must be at least one particle with which it is antiparallel. There is a final category of arrows which is more difficult to interpret: namely those arrows which are neither events nor light signals, and which are not ordered by << (or by <<'). These represent processes which propagate "outside" the light cone, for which there is no arrow of time. One interpretation would be to view them as "virtual particles" as they are introduced in elementary particle theories. Feynman diagrams are indeed invariant for the transformation which inverses the direction of time for those intermediary lines which are called "virtual particles", and hence it does not make sense to ascribe a time ordering to these processes. Another interpretation would be to see the not chronologically ordered arrows as representing tachyons, i.e. (hypothetic) particles which move faster than light, and for which the direction of time can change with the reference system.14 Both interpretations are equivalent in the sense that they presuppose phenomena which--at least in the present situation--cannot be observed. But this should not be surprising, since the determining feature of these arrows which are not chronologically ordered, is that they have no parallel (or anti parallel) path which consists of light signals or particles. If we suppose that the measuring apparatus of the observer is made out of particles, and interacts with the observed phenomenon by exchanging light signals or particles, then we might expect that the processes corresponding with the unordered arrows cannot be directly observed. Besides, the principle that such processes cannot be manipulated by an observer would be sufficient to eliminate all causal paradoxes which are usually associated with the existence of tachyons.[15] (For those people who do not like theories containing "unobservable entities", there is another way of solving the problem of unordered arrows: you can simply eliminate them by introducing some constraint on arrow structures, or by further extending the domain of the precedence relation such that all arrows will be ordered by it. In practice, however, the quality of a scientific language is determined not so much by the observability of all of its terms, but by the universality and simplicity of its descriptions and by the insight they provide).
In order to make closer contact with traditional theories (which are based on the real number system as primary tool for labeling phenomena through the use of coordinate frames), it would be interesting to introduce some quantitative measures into the qualitative descriptions of the structural language. The fundamental structure associated with a number system is a linear ordering. The simplest instances of such linear orderings in the structural description are the linear paths (i.e. without circuits). So in order to label the events on such a path, it suffices to define an order preserving map from the set of events on the path to the set of real numbers. The path can be interpreted as a world line if its order agrees with the chronological order determined by << (or by <<'). The parametrization of the events can then be considered as defining a proper time coordinate on the path.
This can be used to define a metric on the space of events. Consider
a path P, an event e0P,
and a parametrization t: {e P|e event}
-> R such that t(e0) = 0. Consider an arbitrary
event e. We shall suppose that the path P can always
be reached from e by a light path, i.e. there exist events
e1,e2 P
such that e2 -> e. (This amounts to saying
that the event e can be seen by an observer travelling along P,
and vice versa). It is easily shown that these events, which are
the intersections of P and the light cone through e,
are unique: suppose that there is an event e3 P
such that e3 -> e (i.e. there is a light
path between e and e3). The events
of P are linearly ordered by <<, so we have e3
<< e1 or e1 << e3.
Suppose e1<<e3 (the proof for
the second case is analogous). Then you can construct a second path between
e and e3 by concatenating the light path
determined by e -> e1, and the part of P
between e1 and e3. But this is in contradiction
with the hypothesis e -> e3 which implies that
the path between e and e3 is unique, unless e3
= e1. An analogous proof can be given for e2->
e.
Each event e thus determines two coordinates t(e1) and t(e2). With these you can define a function: g: AxA -> R: (e0, e) -> t(e1) x t(e2). g can be interpreted as a space-time metric. It is easily checked that: g(ea,eb)=0 iff the interval between ea and eb is lightlike (i.e. ea -> eb or eb -> ea), >0 iff the interval is timelike (ea << eb or eb << ea), < 0 iff the interval is space-like (all other cases). With some additional hypotheses about continuity, differentiability and dimension, it can be shown that a function constructed in this way on a set of events and a set of parametrized paths reduces to a conformal metric on a conventional space-time manifold.[16]
I have deliberately ignored until now all questions concerning continuity. The
class of arrows is not really a set, and so the notions of finite, denumerable and continuous cardinality have no a priori relevance in this context. This leaves the space open for the "continuous versus discrete" debate (see e.g. 9). Of course, if you are convinced that nature is fundamentally continuous (respectively discrete), you can always choose your structural descriptions such that they agree with that conviction. Even without specifying the cardinality of the event set you consider, it is possible to introduce a topology determined by the open intervals of the << relation, 13 so that the topological concept of "continuity" can be defined. Concerning dimension, it must be possible to represent in a structural manner, the fact that space-time seems to be basically four-dimensional. One method, which is used by Woodhouse,16 is to demand that every event be determined by the intersections of its light cone with two neighbouring parametrized paths, i.e. by four real numbers. It would be preferable, however, to find a construction which is derived more directly from the defining properties of events and arrows. Since each event is determined by its input and output sets, a possible way would be to limit these sets to cardinal number two, so that the event is determined by four arrows, which can be labeled by their intersections with some suitable chosen parametrized paths. This restriction would not be unnatural if such an event is considered as a scattering between two elementary particles, represented by two incoming and two outcoming arrows. This 2 x 2 construction with its binary character resembles in certain aspects Finkelstein's "checkerboard model" of space-time.9
We have been able to express the geometrical features of an arrow, i.e. to label it by its "localization" in the global space-time framework abstracted from the graph of all arrows. This is a way of characterizing an arrow by the relations of precedence and distance it has with all the other arrows (or with a chosen reference set). There are however, other ways of characterizing an arrow (or the physical process it stands for), which are more local, in the sense that they use only the relations with the arrows in its immediate neighbourhood. The characteristics or properties determined in such a manner are therefore independent of the space-time position of the arrow, and can be the same for arrows with different localizations. For example, to determine whether an arrow is an event, it suffices to check if its set of contiguous arrows contains no other element than itself. In fact, any physical observation amounts to the establishment of such a local relationship between the observed phenomenon and an observation apparatus. The structure of the apparatus determines the physical property which is observed.
For example, if you want to determine whether a certain particle has electro - magnetic properties (e.g. charge or magnetic moment), you use an electromagnetic field and see if there is an interaction. If a photon is scattered by the particle, you may conclude that the particle has the property in consideration. In structural terms, this means that there was an event e, with two input arrows, one representing the particle, the other one the photon, which is connected to an arrow, representing the scattered photon, which is itself connected to the observer via a causal path (i.e. ordered by the causal precedence). The existence of such a structure, together with the knowledge that the arrow which is input contiguous with the arrow of the observed particle, is a photon, is sufficient to establish the fact that particle has electromagnetic properties. In this way this property is reduced to a structural relationship between an arrow which is to be determined and an arrow which is known by the observer to be a photon. This "knowing" itself is again a structural relationship between the photon arrow and the structure representing the observer (e.g. the photon can interact with the molecules of the retina of the observer). The observer is here seen as one complex dynamical pattern out of the many which are found in the universal arrow structure. No undescribable, extraphysical entities such as "consciousness" or "mind" must be introduced.
What I want to argue here is that every property (or predicate) an observer attributes to a phenomenon can ultimately be reduced to an invariant structural relationship between the observer and the phenomenon. You could say that the observer disposes of a certain structure, which is materialized partly in his measurement apparatus, partly in his sense-organs, partly in his brain, and waits for a phenomenon to fit this structure. If the phenomenon fits, then its pattern is recognized, and it is attributed to the corresponding property (e.g. being charged). If it does not fit, the absence of the property is noted. Such an observational structure is what Piron calls a "question".5 It indeed "asks", or tests whether the phenomenon has the given property. One could also call it a cognitive structure, since it represents one of the basic mechanisms with which we know the phenomena. In general, however, there will be different observational structures which determine the same property: e.g., there are many ways to measure a charge. That is why Piron defines a "property" as a class of equivalent "questions". One could then wonder whether these equivalent questions would have some "common denominator", some elementary substructure which would be characteristic for all of them. If one could succeed in uncovering this structure, one would dispose of a very fundamental, structural characterization of the property in consideration. This is what I have tried to do, for example, when I have defined the property of "travelling with the speed of light" as a structural characteristic of certain arrows. Let us call such a primitive observational structure a "property structure". It could be thought of as a system of arrows, representing potential information transferring processes, with a certain input structure, representing the phenomenon to be observed, and one output arrow, representing the transfer of one bit of information determining whether the answer to the "question" was "yes" or "no". This output process can be viewed as the "click" of a measuring device (e.g. a photon detector), or as the firing of a neuron in the brain of the observer.
The relations between different property structures will determine the logic of observed properties. E.g. if two property structures a and b are such that any phenomenon which fits a will also fit b, then the property a can be said to imply the property b. It is on this level of description that the basic structures of quantum mechanics are to be introduced, as is shown for example in the work of Piron5 and Aerts.6 Since an arrow is determined by its environment. it will be different if its environment is changed, e.g. if it is fitted to an observational structure. This verifies the quantum mechanical principle that a general observation changes the state of the system which is observed. It is also clear that an arrow in general cannot be incorporated in two different obervational structures without mutual interference. This accounts for the fact that quantum observables are generally incompatible.
Another characteristic feature of quantum systems is that, in between observations, they are not localized in a definite point of space-time. In the structural description, however, space-time is not an absolute frame in which every phenomenon has its proper place, but a superstructure consisting of a set of relations between a preferred class of phenomena: the events. A general phenomenon, represented by an arrow, has no space-time localization: it just travels from one event, to another one, but it is meaningless to ask where it has been in between: space-time is not defined outside the events. If nevertheless one wants to localize a particle between two interactions by forcing it into an observational structure and in this way creating an event, then he can expect that the answer will not be completely determined by its "initial state", but will depend upon the new environment which is created, i.e. upon the measurement apparatus and everything which is connected with it.
In the structural description there is also room for the apparently non local interactions which are characteristic of certain quantum effects, such as the EPR paradox1 and the Aharonov-Bohm effect.2 We have indeed seen that there exists a special class of arrows outside the light cone which represent a kind of "virtual processes". Although they are not directly observable, these processes might be viewed as carrying certain "non local influences" with a "speed" faster than that of light.
In this section I have tried to argue that the structural language is flexible enough to allow the description of an important class of fundamental phenomena, which are difficult to incorporate in a conventional "geometrical type" of representation. The actual implementation of these descriptions, however, is yet to be started.
I have argued that the failure of present-day models to establish satisfactory foundations for physical theory, is due to a basic shortcoming of the language they use. To overcome this problem I have proposed to construct a new language, which is not lexical (i.e. based on a lexicon, or set of meaningful elements) but structural (i.e. based on the structures, the coherent patterns formed by the connections of elements which are intrinsically meaningless). The main advantage of this structural language is that its descriptions start directly with the level of dynamics, with the elementary processes and the irreducible patterns they form, whereas the conventional description reduces this dynamical, holistic world to a combination of independent, static pieces.
The advantage of the traditional, analytic language lies in the fact that, through centuries of experimentation, its relation with practical observation has been elaborated in great detail. The structural language as I have exposed it here on the other hand, has purely theoretical antecedents, which are of a rather philosophical or formal nature. If this language is to be used for the description of concrete phenomena, its relation with observation should be clearly specified. The simplest way to do this through the intermediary of the traditional language, which at one extremity of its spectrum of applications, describes the concrete operations needed to carry out a measurement, while at the other extremity it gives a very complicated and abstract picture of the fundamental dynamic pattern. So, to interpret the structural language in a concrete way, it is sufficient to reverse the traditional sequence: observation -> subjects and predicates -> logic -> geometry -> dynamics.
I have carried out the first step of this program in some detail, and shown how most of the conventional space-time geometry can be reconstructed out of the elementary patterns of the structural expressions. This procedure exemplifies one of the distinctive qualities of the structural description, namely that physical structures arise in a very simple and natural way, that it is not necessary to introduce external constraints (axioms or postulates) to find a model which has the required properties. For example, in the manifold description of space-time one usually introduces the axiom that no timeline path can be closed. In the structural description, on the other hand, the definition of a timeline path is such that it cannot be closed, and thus no axiom is needed. One could answer to this by remarking that in a formal system an axiom is merely a kind of implicit definition, that the formal objects of the system are determined by the axiomatic constraints which relate them. The system would however be much easier to handle if all definitions were explicit, if no outside constraints had to be added. The aim of the structural description is just this: to reduce every "concept" or "formal object" we use to an invariant, abstract structure which embodies all relations or constraints in an explicit form. In fact, what we call "laws of nature" or "basic principles of physics" are merely constraints imposed on the system of concepts (i.e. subjects and predicates) we use to describe our observations. They thus act as implicit definitions. For example, the concept of "baryon number" would be devoid of meaning if there were not a constraint on elementary reactions which is called "the law of conservation of baryon number". In this special case the implicit definition can easily be made explicit: a baryon number is an additive parameter such that the known conservation law is obeyed. In general, however, the network of constraints which implicitly determines a given concept is much too complex and too less known to be reduced to an all-inclusive explicit definition. In the ideal case where such a reduction could be carried out for all physical concepts, all "laws of nature" would reduce to tautologies, to trivial propositions. The structural language can be seen as an instrument for facilitating such an enterprise.
Even with this instrument, however, the task remains very difficult. For example, when I tried to represent the fact that space-time is four-dimensional, I had to introduce some external constraint on the structural description. Nevertheless, one could expect that after a more thorough structural analysis of the concept of dimension it would appear, either that the four-dimensionality of space is not as absolute as it looks (e.g. that it only appears statistically, on a macroscopic scale), or that the structural description in its present version is not as fundamental as it should be (e.g. one might find that any structure can be replaced by another structure in which all input and output sets have only two elements, or that the definition of an event should be changed).
This type of analysis has many similarities with an approach which is known as "Structuralism",[17] and which has its roots in the fields of linguistics and anthropology. It is mainly concerned with the study of the structures of sociocultural systems, such as languages, myths, family systems, literature, etc. The problem with this approach, which is basically limited to the so-called "human sciences", is that it lacks a proper formalism in which its results can be expressed without ambiguity. Possibly some version of the structural language may provide such a formalism.
A similar remark can be made about a recent approach, which is related to the preceding one, but which has begun to grow into a proper discipline called "Cognitive Science"[18]. This newly emerging science has its origin in such diverse fields as computer science (especially artificial intelligence), epistemology, psychology, logic and linguistics. Its aim is the study of the processes and structures through which information about the outside world is obtained, processed and stored for later use by an intelligent system, such as a human being. This includes the study of how we perceive, think, understand, imagine, interpret,... of how memories, thoughts theories and languages are formed and how they evolve.
You will notice that the problem of observation and attribution of properties in physics, as I have sketched it in the preceding section, falls under this heading. Physical observation is indeed concerned with the acquisition, recognition and interpretation of data about external phenomena. The difficulties encountered in studying these problems, as well in physics as in cognitive science, are due not so much to a lack of formal languages (there are numerous formalisms, inspired mostly--in physics--by geometry and analysis,--in cognitive science--by logic and programming languages), but to the lack of a language which can express in a simple way the fundamentally dynamical and holistic nature of the cognitive process. This process is indeed characterized by the fact that it cannot be reduced to separate components. If one nevertheless tries to split this information processing structure into subsequent (e.g.: phenomenon, measurement apparatus, eyes of the observer, brain of the observer, "consciousness" of the observer,...) he runs inescapably into conceptual difficulties such as the Schrodinger's cat paradox or the problem of the homunculus. These problems arise because the conviction that a finite process such as an observation, could be analyzed into separate stages, implies that there be some final stage, some subsystem where the cognitive process could be said to terminate. But then we are confronted with the question of where this endpoint is to be located. At what moment may we conclude that the observation has ended (in Schrodinger's terms: that the cat is dead): when the detector clicks, when the sound of the click reaches the ears of the observer, when the observer becomes conscious of the observation? If we choose the last possibility, then where is this consciousness to be located: in some part of the brain of the observer, or in the brain of a homunculus called "Mind", who is busy watching everything that happens in the observer's brain? Such a reasoning clearly leads to an infinite regression: the final stage of the cognitive process is evasive, any attempt to approach it, makes it recede; it seems forever to remain beyond grasp. The only way out of this paradox is to recognize that the act of cognition, the "stream of consciousness", is not located in a definite subsystem, but resides "in between" the different subsystems, it forms a dynamical pattern, which cannot be broken down into parts without losing its identity. It is meaningless to believe that the very process through which "meaning" is ascribed to the phenomenal world, could be analysed into separately meaningful elements. That is why the conventional formalisms which are used by physicists and cognitive scientists and which are based on a subject-predicate scheme, are unable to give a satisfactory description of the process of observation.
The whole problem of the interpretation of quantum theory lies just there: to understand quantum mechanics means to understand the observation process, and this is impossible as long as you use a language which a priori separates observer and phenomenon.[19] However, as I have argued in the preceding section, the structural language possesses the features necessary to allow a holistic description of this problem. Since the same language can be used to understand the structure of space-time, a structural description should be able to reconcile the viewpoints of quantum mechanics and relativity theory and thus to provide the foundations for a unified theory of physical phenomena and their interactions with observers. Of course there is still a long way to go before such a program could be achieved. Firstly, the structural description we have should be extended to include basic cognitive processes. Secondly, the principal dynamic properties of elementary processes, such as mass, momentum, charge,... should be added to the existing representation of space-time structure. To overcome the many difficulties which will be encountered along this way, it will be needed to add and to adapt a lot of features of the structural language, possibly even to change its formal base. These problems to be foreseen may not be as insurmountable as they look. The main reason for optimism is that the structural language, by its very construction, is fundamentally dynamic and flexible. I would like to conclude by stressing the fundamentally transdisciplinary nature of this enterprise. As was already noted during the discussion of cognitive science, the structural analysis of cognitive and physical processes involves ideas from a great variety of scientific disciplines. The only way to make an efficient synthesis of these scattered pieces of knowledge, is to transcend the boundaries which presently divide the scientific landscape. Some future version of the structural language should provide the perfect instrument for transcending these communication gaps between the sciences, which are due to the use of different subject-predicate schemes for description.
I thank Dr. D. Aerts, Prof. L. Apostel and Prof. J. Reignier for taking the time to discuss most of these ideas with me. I am much indebted to G. Fierlafijn, who introduced me to the "semiotic viewpoint", which made me see that it is all a question of language.
1. A. Aspect, J. Dalibard & G. Roger, "Experimental test of Bell's inequalities using time-varying analyzers." Physical Review Letters, 49 , No. 25, December 1982, pp. 1804-1807.
2. R. G. Chambers, "Shift of an Electron Interference Pattern by Enclosed Magnetic Flux." Physical Review Letters, 5, No. 1, January 1960, pp. 3-5.
3. M. Jammer, The Philosophy of Quantum Mechanics. Wiley, London, 1974.
4. C. W. Misner, K. S. Thorne & J. A. Wheeler, Gravitation. Freeman, San Francisco, 1974.
5. C. Piron, Foundations of Quantum Physics. W. A. Benjamin, Menlo Park, California, 1976.
6. D. Aerts , "Classical Theories and Non Classical Theories as Special Cases of a More General Theory." J. Math. Phys., 24, 1983, pp. 2441-2454.
7. R. P. Feynman, "Simulating Physics with Computers." Int. J. Theoretical Physics, 21, Nos. 6-7, 1982, pp. 467-488.
8. T. Bastin, H. P. Noyes, J. Amson & C. W. Kilmister, "On the Physical Interpretation and the Mathematical Structure of the Combinatorial Hierarchy." Int. J. Theoretical Physics, 18, No. 7, 1979, pp. 445-488.
9. D. Finkelstein, "Space-Time Code. IV." Physical Review, D9, No. 8, 1974, pp. 2219-2231. D. Finkelstein, "Space-Time Code. III." Physical Review, D5, No. 12, 1972, pp. 2922-2931. D. Finkelstein , "Space-Time Code. II." Physical Review, D5, No. 2, 1972, pp. 320-328. D. Finkelstein , "Space-Time Code." Physical Review, 184, No. 5, 1969, pp. 1261-1271.
10. R. Penrose, "Angular Momentum: an Approach to Combinatorial Space-Time.", In: Quantum Theory and Beyond, edited by T. Bastin, Cambridge University Press, Cambridge, 1971, pp. 200-210.
11. D. Finkelstein, "Quantum Sets and Clifford Algebras." Int. J. Theoretical Physics, 21, Nos. 6-7, 1982, pp. 489-503.
12. L. Castell, M. Drieschner & C. F. von Weizsäcker, Quantum Theory and the Structures of Space and Time 1-4. Hanser, Munich, 1975-1977-1979-1981.
13. E. H. Kronheimer & R. Penrose, "On the Structure of Causal Spaces." Proceedings of the Cambridge Philosophical Society, 63, 1967, pp. 481-501.
14. E. Recami (ed.), Tachyons, Monopoles and Related Topics. North Holland, Amsterdam, 1978.
15. T. Sjödin & F. Heylighen, "Tachyons Imply the Existence of a Privileged Frame." Lettere al Nuovo Cimento, 44, No. 8, December 1985, pp. 617 - 623.
16. N. M. J. Woodhouse, "The Differentiable and Causal Structures of Space-Time." J. Mathematical Physics, 14, No. 4, April 1973, pp. 495-501.
17. T. Hawkes, Structuralism and Semiotics. Methuen, London, 1977.
18. M. De Mey, The Cognitive Paradigm. Reidel, Dordrecht, 1982.
19. D. Finkelstein, "Holistic Methods in Quantum Logic.", In: Quantum Theory and the Structures of Space and Time 3, edited by L. Castell, M. Drieschner & C.F. von Weizsäcker, Hanser, Munich, 1979, pp. 37-59.
20. F. Heylighen, Representation and Change. A Metarepresentational Framework for the Foundations of Physical and Cognitive Science. Communication & Cognition, Gent, 1990.
21. F. Heylighen, "Classical and Non-classical Representations in Physics". In: Cybernetics and Systems, 21, No. 4, 1990, pp. 423-444.
22. F. Heylighen, "Relational Closure: a mathematical concept for distinction-making and complexity analysis.", In: Cybernetics and Systems '90 , edited by R. Trappl, World Science Publishers, Singapore, 1990, pp. 335-342.
23. F. Heylighen, "Design of a Hypermedia Interface Translating between Associative and Formal Representations", International Journal of Man-Machine Studies (in press), 1990.