This is chapter 6 of the "The
Phenomenon of Science" by Valentin F.
Turchin
Contents:
LET US BEGIN with the most fundamental concept of logic, the concept of the "concept.'' In chapter 2 we gave a cybernetic definition of the concept in its Aristotelian version-as a set of situations at the input of a cybernetic system. To master a concept means to be able to recognize it, that is, to be able to determine whether or not any given situation belongs to the set that characterizes this concept. This definition applies equally to complex cybernetic systems of natural origin about whose organization we have only a general idea (for example: the brain of an animal) and to those relatively simple systems we ourselves create for applied and research purposes.
In the first case we arrive at the conclusion, that the system recognizes a certain concept, by observing external manifestations of the system's activity. For example, when we see that a dog becomes happily excited when it hears its master's voice and responds in a completely different way to all other sounds we conclude that the dog has the concept of ''master's voice.'' This concept develops in the dog naturally, without any special effort by the experimenter. To determine the maximum capabilities of the dog brain the experimenter may create unusual conditions for the animal and watch its reaction. I. P. Pavlov and his school conducted many such experiments. If a dog is shown plywood circles and squares of different sizes and colors and is fed after the presentation of a circle and punished after the presentation of a square, the dog will learn to distinguish the circle and the square and will respond differently when these shapes are presented. Thus, the dog is capable of recognizing certain general (abstract) concepts-in this case the concepts of circle and square abstracted from the features of size and color. This means we must conclude that the dog possesses the abstract concepts of ''circle'' and "square."
But no sooner do we say this than we begin to feel that perhaps this conclusion was too hasty. The statement that the dog can possess the concept of ''master's voice'' (referring, of course, to the voice of a specific person) can be accepted without reservation, but the statement that the concept of square is accessible to the dog seems true in one sense and not in another. We shall take note of this now and return to the question later. In the meantime let us examine the dog's mental capabilities by indicating the very simple concepts known to be inaccessible to the animal. Suppose that you show the dog a box divided into two parts, each of which contains several billard balls. You want to force the dog to distinguish the case where the number of balls in each part is equal from the case where the number of balls in the parts differs. It is a safe bet that no matter how much you feed the dog and no matter how much you beat it you will not achieve your purpose. The concept of different numbers is inaccessible to the dog.
Cybernetic systems possessing the ability to recognize concepts are also created artificially. Their importance is steadily growing in connection with cybernetic science and production. The development of artificial recognition devices (discriminators) plays a crucial part in understanding the general principles and concrete mechanisms of the working of the brain. These devices serve as models with which people try to lift the veil from the process of thinking. The creation of an "artificial brain'' which performs, at least partially, the same functions as the natural brain provides indications of how to approach investigation of the activity of the natural brain. It is interesting that one of the first results of comparing artificial and natural recognition systems was the conclusion that natural systems are very narrowly goal-directed and specialized. Within their own specialization they reach a high level of refinement, but they are completely impotent when the problem goes beyond this framework. Recognizing a person by voice is an extremely difficult problem for artificial cybernetic devices, but the brain of a dog resolves it easily. At the same time the problem of comparing the number of billard balls, which is very simple for an artificial system, is beyond the ability of a dog.
In chapter 2 we considered a cybernetic discriminator that was fed information by signals from light-sensitive receptors arranged on a screen. We called the situation, that is to say the aggregate of values of all signals from the receptors, the ''picture''; it coincides with the image on the screen with a precision down to semitones. This device (picture discriminator) will serve as an illustration in this chapter too.
SO FAR, the examples of concepts we have given have fit within the definition of the concept as a set of situations. But as it turns out, this definition does not apply to every concept that seems intuitively clear to us and manifests itself in language. For example' let us take the concept expressed by the prepositions ''inside'' or ''in.'' For those who do not like to see a concept expressed by a preposition, we can express it by phrases such as "to be located inside" or "location in." This concept is applicable to a device to whose input ''pictures'' are fed.
In figure 6.1 for example, spot A is inside contour B. But can we correlate the concept of ''inside'' to some definite set of pictures? No, we cannot. This can be seen, for example, from consideration of the picture shown in figure 6.2.
In figure 6.2 a spot A is inside contour B, but not inside contour C. In figure 6.2 b, spot A is outside contour B while spot C is inside it.
Could these pictures be classed with a set of situations for "inside" which we would have to construct? Any answer will be unsatisfactory and arbitrary, because the question itself is meaningless. The concept of ''inside'' does not characterize a picture (situation) as a whole but rather the relation between two definite objects. details in the picture. As long as these objects are not indicated, a definite spot and a definite contour, it is meaningless to ask the question ''inside or not'''?
WE SHALL call the concepts that express attributes of the situation as a whole ''Aristotelian,'' because Aristotle's logic is simply a consistent theory of the correct use of such concepts. For each Aristotelian concept there is a definite corresponding set of situations, specifically those situations in which the attribute expressed by this concept occurs. Therefore the Aristotelian concept can also be described as a certain set or class of situations (phenomena, objects in that extremely general sense in which these terms are used here; they are all equivalent to one another and to the term ''something'' [in Russian nechto] which is the most precise but also the most inconvenient because of the difficulties with Russian grammar its use entails). Therefore all the laws of Aristotelian logic can also easily be derived from the simplest properties of operations on sets.
For example, let us take the classical syllogism:
All men are mortal
Socrates is a man
Three Aristotelian concepts participate in this reasoning: ''man,'' ''mortal,'' and ''Socrates.'' The concept of ''man'' is characterized by the set of situations in which we say, ''This is a man.'' The same thing applies to the other concepts. To make the properties of the sets graphically clear let us represent each situation as a point within a certain square, as is shown in figure 6.3.
Then this square will embody the set of all conceivable situations corresponding to the maximally general concept ''something.'' The other concepts, to which deterrent sets of points correspond, will be shown by different areas inside the square. The statement that ''all men are mortal,'' in other words ''every man is mortal," signifies that every point included in the area of ''man'' is also within the area of ''mortal'' (''mortal being''), which is to say that the ''man'' area is entirely inside the ''mortal'' area. In exactly the same way the second premise of the syllogism means that the ''Socrates'' area is entirely inside the ''man'' area. It follows from this that the ''Socrates'' area is within the ''mortal'' area, or in other words the statement "Socrates is mortal'' is true.
Figure 6.4 demonstrates the correctness of the following deduction rule (''disamis'' in logical terminology):
All A are B
Some A are C
Aristotle's logic played an important role in the development of European culture. But it does not go deeply enough into the structure of our thinking: it is not able to reflect the process of breaking situations up into distinct parts (objects) and investigating the relations among these parts. In discussing the attributes of objects Aristotelian logic is completely adequate, because an isolated object can be pictured as a certain situation.
Forming the set of such situation-objects, we obtain an abstract concept that expresses one of the properties of the object. Things are different with relations. Aristotelian logic can express the concept of the aggregate of objects which are in a given relation, but it has no means for expressing the concept of the relation as such. We can represent a set of pictures that have the form of contours with spots in the middle; this set generates the Aristotelian concept (attribute) of ''being" a contour with a spot in the middle.'' But there is no Aristotelian concept for ''being inside.'' Aristotle's logic is too global and superficial.
Let us take the following deduction:
Ivan is Peter's brother
The inference is correct, but to substantiate it one must state openly the premise which is taken for granted here: that the relation of ''brothers'' is symmetrical. This premise can be expressed by the phrase: ''If x is the brother of y, then y is the brother of x ."
In this the letters x and y, represent any persons of the male sex. But this symbolism goes beyond the limits of Aristotelian logic.
Can this syllogism be expressed in the language of Aristotle's logic? It can if we consider not individual people but pairs of people-or, more exactly, ordered pairs, which is to say pairs where one person is assigned the number one and the other receives the number two. Here is this syllogism, which is completely proper from the point of view of Aristotelian logic.
The pair (Ivan and Peter) possesses the attribute: the first is the brother of the second
Each pair possessing the attribute: ''the first is the brother of the second'' possesses the attribute: ''the second is the brother of the first''
Even though formally it is the same reasoning used before, this clumsy syllogism misses the mark because it does not reflect the main element in our initial syllogism, the symmetry in the relation of ''brothers.'' The attributes ''the first is the brother of the second'' and ''the second is the brother of the first'' are in no way broken down, in no way connected with one another, and in no way connected with the fact that they are applied to objects which have the appearance of an ordered pair.
It was not accidental that we began our cybernetic investigation of concepts from Aristotelian concepts. They are simpler because they permit definition exclusively in terms of input and output states without referring to the internal structure of the recognition system. The same thing occurred in the history of human thought. People first became aware of the existence of Aristotelian concepts: awareness of relations came only much later.
Because the chief thing in mathematics is to investigate relations among objects, Aristotelian logic is completely inadequate for expressing mathematical proofs. This was noted long ago; the examples from mathematics which traditional logic uses speak for themselves: they are extremely primitive and uninteresting. Until the very end of the nineteenth century, when a new (''mathematical'') logic began to be created, mathematics and logic developed independently of one another.
IN PHILOSOPHY Hegel delivered the decisive blow against Aristotelian logic. With his dialectic he showed that the world must be viewed not as an aggregate of objects that possess certain attributes, but rather as an aggregate of objects that stand in certain relations to one another. This does not exclude attributes from consideration, of course, for the concept of the relation is much broader than the concept of the attribute.
A relation may be defined for any number of objects. Specifically, the number of objects may be one; such a relation is an attribute, a property. Pair relations, that is to say relations between two objects, are the clearest intuitively and at the same time the most important. Two is the minimum number of objects for which the relation ceases to be an attribute, and becomes a relation proper. The number two lies at the foundation of the Hegelian method, which is reflected in the very term ''dialectic."
The most important features of Hegel's dialectic follow directly from the description of phenomena in terms of relations, not attributes. Above all, what follows from this approach is the theory of the interaction and interrelatedness of everything that exists. Further: If two elements are in correspondence and do not contradict one another, they act as something whole and their common attributes become paramount while the interaction, the relation, between them withdraws to a secondary position. Relations among elements. objects, manifest themselves to the extent that they are relations of opposition, contradiction, and antagonism. Thus, the idea of the struggle of opposites plays an important part in Hegel.
When considering the relation between the state of an object at a given moment and the state of this same object at some other moment in time we come to the concept of change. Change is the relation between objects separated by a time interval. In the language that operates with attributes but not with relations. change cannot be expressed. The most that such language is capable of is depicting a series of states of the object which are in no way interconnected.
Zeno's aporia concerning the arrow in flight is a brilliant expression of this inability. Let us consider the arrow in flight. Take a certain moment in time. At this moment the arrow occupies a definite position in space. Take another moment. The arrow again occupies a completely determinate position in space. The same thing is true for any other moment. This means that the arrow always occupies a definite position in space. This means that it is standing in place. In Aristotelian concepts the world is represented as something static, frozen, or at best mechanically duplicated with certain variations. On the other hand, having made the investigation of relations its object, the dialectic studies things from the point of view of their change. movement, and development. It discloses the historical causality and relativity (from the word ''relation''!) of things which are represented as unconditional and external when described in Aristotelian concepts. Combining the concept of opposition with the concept of the relation among states at successive moments in time generates the concept of the negation and the concept of the negation of the negation. The dialectic is dynamic and revolutionary.
In relation to Aristotelian logic, Hegel's dialectic acted as a destructive force-and not just because of its ''general'' revolutionary nature but also because it pointed out the many contradictions that arise when a description of phenomena which demands the language of relations is squeezed into the narrow framework of the language of attributes. In Hegel and his followers these contradictions were often surrounded with a certain exalted aura and, one might say, a semimystical significance. This reflected, on the one hand. the idealistic orientation of Hegel's philosophy, and on the other hand a general characteristic of new doctrines, theories, and movements: in the initial stages of their development, trying to liberate themselves from the old intellectual framework, they prefer a paradoxical, exaggerated form and become heroic and romantic. Hegel's dialectic is the heroic epoch of the new logic, when the old logical formalism had been broken but the new one was not yet created. Therefore things seemed contradictory and not subject to formalisation (''dialectical'') which later proved to be beautifully ordered and formalized. To modern thinking, which makes free use of the language of relations and is armed with analysis of logical concepts and constructions, the He~elian style of thinking appears as obscure philosophizing about things which are clear. The following reasoning is a crudely simplified, caricature-like sketch of the Hegelian dialectical contradiction, showing the source from which this contradiction arises.
''Let us put the question: is the number 1,000 large or small? It is large because it is much more than one. It is small because it is much less than 1 million. This means that it is both large and small at the same time. A dialectical contradiction. What is large is at the same time not large, A is not-A.''
The concepts of ''large'' and ''small" were considered here as attributes of objects (numbers). In fact these are not attributes but concealed (by means of the grammatical category of the adjective) relations. An exact meaning can be given only to the concepts "larger'' and ''smaller.'' If we analyze the reasoning given above from this point of view it will prove to be simply nonsense. This caricature was not directed against Hegel (the credit due him for creating the new logic is indisputable) but rather against those who take an uncritical attitude toward Hegel's dialectical method and, in the second half of the twentieth century, propagate the style of thinking of the first half of the nineteenth century, ignoring the enormous progress made by logic in this century and a half.
THE DECISIVE FACTOR in the advance of logic was the development of mathematical logic in the late nineteenth and early twentieth centuries. This process was generated by the needs of mathematics and was carried out by mathematicians. The gap between mathematics and logic was finally overcome. Having expanded its language and made it mathematical. Logic became suitable for describing and investigating mathematical proof. On the other hand, mathematical methods began to be used to solve logical problems.
Having gained a base of operations in the field of mathematics, the new logic began to penetrate the natural sciences and philosophy. In this process the role of the mathematical element proper (the use of mathematical methods) declined. Nonetheless all modern logic is often called ''mathematical'' because of its language and origin.
BEFORE GOING on in our analysis of language and thinking we need to give a short sketch of modern logic and those concepts which are related to language. For now we will leave the concepts related to the logical deduction (proof) aside.
Modern logic divides everything that exists into objects and statements. In natural language statements are represented by sentences or groups of sentences and objects are depicted by words or combinations of words which make up the sentences. Examples of objects are ''heron,'' ''Uncle Kolya," or ''kolkhoz chairman.'' Examples of statements are: ''The heron died,'' or ''Uncle Kolya was elected chairman of the kolkhoz.'' Objects are most often expressed by nouns, but this is not mandatory. For example, in the statement ''To smoke is harmful,'' ''to smoke'' is the object. In application to mathematics objects are usually called terms and statements are called relations. Examples of terms are:
(1) 3.14;
(2) ax2 + bx + c;
(3) ![]() f(z)dz.
f(z)dz.
Examples of relations are:
(1) ax2 + bx + c = 0;
(2) 0 < z <= 1,
(3) no matter what natural number n > 1 may be, a simple number p will be found which is a divisor of number n;
(4) the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse.
In logic the concepts ''object'' and ''statement'' are considered primary, intuitively clear, and indefinable. The formal difference between them is that a statement may be said to be true or false. Thus, the examples (3) and (4) of mathematical relations above are true, while the first and second may be true or false depending on the values of the variables x and z. The concepts of truth and falsehood are not applicable to objects.
In logic objects and statements, which are considered elementary-meaning that they cannot be broken down into distinct constituent parts-are represented by letters. Objects are usually represented by small letters and statements by capital letters. We shall follow this system but we shall introduce one more convention. For clarity in writing and to reduce the number of verbal explanations we shall sometimes designate elementary objects and statements with words and phrases within quotation marks. Therefore phrases in quotes will be considered equal to letters.
Objects and statements which are not elementary are obviously constructed from other objects and statements. We must now point out the methods of construction. Where there are two types of elements (objects and statements) and assuming that the elements serving as building material all belong to one type, we find that there are four possible types of constructions. We have reduced them to the following table.
| What Is Constructed | What It Is Constructed From |
Name of the Construction |
| Statement | Statements | Logical Connective |
| Statement | Objects | Predicate |
| Object | Statements | -- |
| Object | Objects | Function |
THERE ARE FIVE widely used logical connectives. Negation (depicted by the symbol -), conjunction (sign &), disjunction (sign V), material implication (sign =>), and equivalence (sign <=>).
The statement -A (read ''not A'') means that statement A is false. In other words, -A is true when A is false and it is false when A is true. The statement A & B (read ''A and B'') signifies the assertion that both A and B are true. It is true only if both statement A and statement B are true.
The statement A V B ("A or B" ) is true if at least one of the two statements A and B is true.
The statement A => B is read ''A entails B'' or "if A then B.'' This is untrue if A is true and B is false but is considered true in all other cases.
Finally, the statement A <=> B is true if statements A and B are either both true or both false.
Parentheses are used to designate the structure of connections, similar to the way they are used in algebra to designate the order of performance of arithmetic operations. For example, the statement -A & B means "S is untrue but B is true,"while the statement - (A & B ) means ''it is untrue that both A and B are true.'' And, just as in algebra, an order of seniority among connectives by the tightness of the bond is established to reduce the number of parentheses. Above we listed the connectives in order of decreasing tightness. For example, the conjunction is a tighter bond than implication and therefore the statement A => B & C is understood as A => (B & C). not as (A => B) & C. This corresponds to algebra where A + B x C is the same as A + (B x C), but not the same as (A + B) x C.
Let us give a few examples of composite statements. A common Russian tongue-twister is ''The heron withered, the heron dried, the heron died'' [in Russian, ''tsaplya chakhla, tsaplya sokhla, tsaplya sdokhla'']. This statement may be written as follows: ''The heron withered'' & ''the heron dried'' & ''the heron died." The relation 0<Z< 1 is the conjunction ''Z>0'' & ''Z< 1,'' while the relation |Z| > 1 is the disjunction ''Z> 1"V''Z<-1Z<-1.'' The definition given above for the logical connective <=> can be written as follows:
[(A <=> B) => (A & B) V (-A &-B)] & [(A & B) V (-A &-B) => (A<=> B)]
We will let the reader translate the following statement into conventional language: ''The light is turned on'' & ''the bulb is not burning'' => ''there is no electricity" V ''the plugs have burned out'' V ''the bulb is burned out.'' If we consider that statements can only be true or false, and consider nothing else about them, then the connectives we have listed are enough to express all conceivable constructions made of statements. Even two connectives are adequate-for example, negation and conjunction or negation and disjunction. This situation obtains, in particular, in relation to mathematical statements. Therefore other connectives are not used in mathematical logic.
But natural language reflects a greater diversity in the evaluation of statements than simply separating them into true statements and false. For example, a statement may be considered meaningless or implausible even though it is possible ("There are probably wolves in this forest''). Special branches of logic which introduce other connectives are devoted to these matters. For modern science (unlike classical mathematical logic) these branches are not very important and we shall not deal with them.
A CONSTRUCTION that associates a statement with certain objects is called a predicate. Predicates are divided into one-place, two-place, three-place, and so on according to the number of objects they require. Functional notation is used to represent them. The predicate can be written as a function with unfilled places for variables, for example:
P( ),
L(, ),
I( , , )
or in the form
P(x),
L(x, y),
I(x, y, z)
having stipulated that x, y and z are object variables, that is, symbols which must in the last analysis be replaced by objects-although which objects is not yet known. But the second form of notation, strictly speaking, no longer represents a predicate; rather, it is a statement containing object variables. In addition to capital letters we shall also use words and phrases within quotation marks, for example: ''red'' (x) or ''between" (x, y, z) and special mathematical signs such as < (x, y).
The one-place predicate expresses an attribute of an object while a predicate with more than one variable expresses a relation among objects. If the places for variables in the predicate are filled then we are dealing with a statement which asserts the existence of the given attribute or relation. The statement ''red'' (''ball") means that the ''ball'' possesses the attribute ''red.'' The construction < (a,b) is equivalent to the relation (inequality) a < b. By joining predicate constructions with logical connectives we obtain more complex statements. For example we formerly wrote the |Z| > 1 without breaking the statement down into elements, but now we write it
> (z, "1" )V < (z, "-1" )
IN MATHEMATICS a large role is played by assertions of the universality
of a given attribute and of the existence of at least one object that possesses
the given attribute. To record these assertions the following so-called
quantifiers are introduced: universal quantifiers 
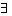

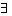
A variable included in a statement under the sign of a quantifier is called a bound variable, because the statement does not depend on this variable just as the sum
Sum (i=n to m) Si
does not depend on the indexes i. The bound variable may be replaced by any other letter that does not coincide with the remaining variables and the meaning of the statement will not change as a result. A variable which is not bound is called free. The statement depends entirely on the free variables it contains.
Here are some examples of statements containing quantifiers.
1) (

For every x and every y, if x is the brother of y and y is a man then y is the brother of x.
2) If D(x, y) is used to represent the statement ''x is a divisor of y,'' then one of the relationships cited above as an example of a statement will be represented in the form
(
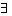
((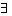

The last relation is true for any statement W(x) and shows that there is a connection between the universal and existential quantifiers. From the existence of object x for which W(x) is true it follows that the assertion that ''W(x) is untrue for all x" is not true.
A quantifier is also, in essence, a logical connective. The attribution of a quantifier changes a statement into a new statement which contains one less free variable. The difference from the connectives we considered above is that one must indicate, in addition to the statement, the free variable that must be coupled. The coupling of a variable means that concrete objects will be put in its place. If the number of objects that can be substituted for the variable is finite then the quantifiers can be viewed simply as convenient abbreviations because they can be expressed by the logical connectives of conjunction and disjunction. Suppose variable x can assume ~l values, which we shall designate by the letters x1, x2, . . . , xn. Then the following equivalences will occur.
(
(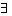
THE THIRD LINE of our table describes a construction that correlates an object to a statement. In natural languages this construction is very widely used. When we say ''red ball,'' we have in mind an object "ball" which possesses the attribute ''red,'' that is, it is such that the statement ''red'' (''ball'') is true. We transfer the statement about the object to the adjective which modifies the noun by which we designate an object; in other cases this can be achieved by participles, participial constructions, and constructions with the connectives "which'' and "such that." If we carry this analysis further we shall find that the noun, like the adjective, indicates first of all a definite attribute or attributes of an object. Like the word ''red,'' the word ''ball'' depicts a certain class of objects and may be correlated to a one-place predicate, "is a ball'' (x), or simply "ball'' (x). Then ''red ball" is such an object that the statements ''ball'' (a) and ''red'' (a) are true; in other words, the statement ''ball'' (a) & "red" (a) is, true.
Notice that there are three independent elements operating in the logical notation: the letter a and the objects ''ball'' and ''red,'' while in writing in natural language there continue to be just two, ''red'' and ''ball.'' But the letter a, which is introduced in logical notation to identify the given object and distinguish it from others (and which is called the identifier), does not completely disappear in natural notation. It has been transferred to the concept ''ball,'' changing it from an attribute to an object' Unlike the word ''red,'' the word ''ball'' identifies; you can say, ''This is the ball we lost yesterday'' or I have in mind the same ball I was talking about in the previous sentence."
But what is an ''object''?
EXPERIENCE TEACHES US that the world we live in is characterized by a certain stability and repetition (and also, of course, by constant movement and variation). Suppose we see a tree. We walk away from it and the image of the tree on the retina of our eye changes in relationship to our movements. This change follows a definite law which is very familiar to us from observation of other objects. But when we return to our former place the image becomes almost exactly the same as it was before. Then we say, ''This is the tree,'' having in mind not only the image of the tree-the mental photograph-at the given moment in time but also the situations at nearby moments. If we are talking about classifying distinct situations by themselves, without considering their relations to other situations, then there is no difference at all between the noun and the adjective; the concept ''ball,'' just like the concept ''red,'' is completely defined by indicating a certain set of situations, and the discriminator (natural or artificial) of these concepts need only be able to use the following sentences correctly: ''This is red,'' ''This is not red,'' "This is a ball," and ''This is not a ball.''
It is different when we must classify time sequences of situations rather than separate situations; we shall represent them as if they were a movie film whose frames each depict the situation at a given moment. In the movie film ''ball'' is not simply a detail of the situation in one frame; it is a detail that recurs in many. The discriminator of the concept ''ball'' cannot simply say, ''Yes, my friends, this is a ball!'' It must identify the particular details in the frames, saying: ''Here is how the ball looks in frame no. 137; here is the same ball in frame no. 138; here it is again in frame no. 139; and here is what it looked like in frame no. 120,'' and so on. The detail of the situation which is called ''the same ball'' can change quite considerably because of change in the position of the eye relative to the ball or a change in the shape of the ball itself, but the ball itself is invariably and absolutely the same. This invariability reflects the relative and temporal invariability we find in reality. It is as if we were to draw a line in time connecting the details in the different frames of film and declare that everything on this line is ''the same'' object. It is this line, in combination with a certain set of attributes (characteristics), that forms the concept of the physical object.
The logical concept of the object reflects a property of physical objects-they preserve their identity. The object of logic is simply an identifier. Sameness is its only attribute, as reflected in our imaginary connecting line. If there are several different classes of objects, then various types of identifiers are ordinarily used to denote the objects in different classes. For example, line segments will be represented by small letters, points by capital letters, angles by Greek letters, and so on. But more concrete attributes characteristic of objects are written in the form of distinct assertions which include the introduced designations. This makes it possible to get by without a construction involving the connective ''such that.'' It is true that at the very beginning of his famous treatise Eléments de mathematique Bourbaki introduces the designation [tau]x[A(x)] for a certain object which possesses attribute A(x), that is, such that A{[tau]x[A(x)]} is a true statement. After this, however, the designation disappears from his text. Thus a definite name for the construction that associates an object with a statement has not even been established and we are forced to leave a blank in our table. In the last analysis, a complete division of labor between identifiers and statements is more convenient.
For example let us take the sentence: ''The reddish-brown dog of Lieutenant Pshebyssky's widow killed the stray cat.'' When written in the language of logic this sentence breaks down into several statements which are implicitly contained in it and expressed h! means of the grammatical category of attribution. They can be joined into one statement using the conjunction sign, but we can obtain a more conventional and readable notation if we simply write out all the assertions being made-each on a new line separated by commas instead of conjunction signs. Assuming that the meaning of the attributes and relations being introduced is clear from the context, we receive the following equivalent of the above sentence:
"dog'' (a),
"reddish-brown'' (a),
"belongs'' (a, b),
"widow'' (b, c),
"Lieutenant Pshebyssky" (c),
"killed'' (a, d),
"cat'' (d),
"stray'' (d).
IN THE EXAMPLE, the predicate, Lieutenant Pshebyssky (c), is the only one that is plainly not elementary. In the attribute ''to be Lieutenant Pshebyssky'' we distinguish two aspects: to have the rank of lieutenant and to have the surname Pshebyssky. That is why this predicate is expressed by two separate words. Of course, we could have put each of these words in the form of a distinct predicate, but the fact that ''lieutenant'' is the rank of object c and ''Pshebyssky'' is the surname of it would not have been reflected in this case, and therefore we considered such a separation meaningless.
''Surname'' and ''rank'' are examples of a function of one free variable of a construction that juxtaposes the object which is the meaning of the function to the object which is the free variable. The function is written, as customary in mathematics, ''surname" (x), "rank'' (x), and so on. If there are several free variables they are separated from one another by commas, after which we are dealing with the function of several variables. This construction associates an object-value with a set of object-variables (their order is important!). An example of a function of two free variables is ''the result of a game of chess'' (x, y). Let us give examples of functions from mathematics. Functions of one free variable: sin (x), |x|; |functions of two variables: arithmetic operations which may be written + (x, y), ~ (x, y), and so on; the distance (A, B) between two points in space A and B; a function of three variables: the angle formed at point B by paths to points A and C: the designation < (A, B, C), abbreviated as < ABC.
Not every object can be substituted into the given function as a free variable or variables. If object a is a reddish-brown dog, then obviously the construction "rank'' (a) is meaningless. The construction + (a, B) is also meaningless where a is a number and B is a point in space. The set of objects (or sets of groups of objects) that can be free variables of a function (or functions) is called its domain of definition. The domain of definition of the function ''rank'' (x) is formed by all those objects which are military servicemen. The objects which can be values of the given function form the set which is called the area of values of the function. The area of values of the function "rank'' (x) includes such objects as "ensign,'' "lieutenant,'' "major,'' and the like, but it cannot include ''3.14'' or ''reddish-brown dog.'' The function "rank" (x) ascribes a definite rank to each serviceman.
When we deal with functions, one of the relations among objects, the relation of equality, becomes particularly important. It is essential for establishing correspondence between functional constructions and the names of objects from the area of values of the function. When singling out an equality from the mass of other relations, we preserve its conventional notation x = y instead of writing it in the form of a predicate = (x, y). The fact that object c has the surname ''Pshebyssky'' and the rank ''lieutenant'' will look as follows:
(''surname'' (c)= "Pshebyssky'') &
(''rank" (c)=''lieutenant'')
The equality relation can be defined formally by the following four assertions.
1. (
2. (

3. (


4. (

The last assertion is true for any statement W(x) which depends on variable x. As an exercise we suggest that the reader translate these assertions into natural language.
In one of the examples given above we introduced the predicate D(x,y), which has the meaning ''x is a divisor of y." The concept of divisibility is wholly determined by the operation (function) of multiplication: therefore the predicate D(x,y) can be expressed by the function x. The natural (that is, whole positive) number p is a divisor of the number n when and only when there exists a natural number m such that n =pxm. In the language of predicate calculus
(

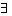
To each function from n free variables we may correlate an n + 1 = place predicate which expresses the relation where one (for example the last) free variable is the given function from the remaining variables. For example, corresponding to function x(x,y) is the predicate M(x, y, z), which yields a true statement if and only it z = x X y. In the general case, corresponding to the function F(x, y, . . .z) there is the predicate F(x, y, . . .z, u), which possesses the property:
(



The predicate F in fact expresses the same concept as the function F. Any statement which contains functional symbols can be rewritten, using predicate symbols only and introducing a certain number of additional object variables. Thus neither of the constructions that generate new objects-the construction with the connective ''such that'' and the function-is essential in principle, and it is possible to get along without them. Unlike the construction ''such that,'' however, functional symbols are very convenient and they are used extensively in logic.
IN CONCLUDING our short sketch of logic we shall consider the question of the relation between the language of logic and natural language. In the course of our discussion the important concepts of the syntax and semantics of language will be introduced.
Let us recall the sentence about the reddish-brown dog, which we expanded into a set of statements expressed by means of predicates. The meaning of this set coincides with the meaning of the initial sentence, but the form of notation, the structure of the text, differs fundamentally. In semiotics (the science that studies sign systems) the aggregate of rules of construction of language elements is called its syntax and the relationship between language elements and their meanings is called semantics. Thus, the first thing that strikes one's eye in comparing logical and natural language is that the language of logic has a different syntax-one that is simple and uniform. It is based on the style of notation which has taken shape in mathematics; the construction of more complex language elements from simpler ones is represented by analogy with mathematical notation of operations and functions. The syntax of the language of logic is completely formalized, that is, there is a set of precisely formulated rules with which one can construct any language element. Moreover, no matter what correctly constructed language element (object or statement) we may take it will always be possible to re-create the element's construction. This process is called syntactical analysis of the element. It is easy to see that syntactical analysis is extremely simple and unambiguous in the language of logic.
The syntax (in the semiotic sense) of natural language is its grammar-that is, the rules by which sentences are constructed from words (syntax in the narrow, linguistic sense of the word) and the rules for constructing words from letters (morphology). Unlike the language of logic, the syntax of natural language is far from completely formalized. It includes an enormous number of rules with an enormous number of exceptions. This difference is entirely understandable. The language of logic was created artificially, while natural language is a result of long development which no one controlled consciously, in which no preconceived plan was used. The grammar of natural language has not been constructed or designed; it is an investigation of an already complete system. an attempt to discover and formulate as clearly as possible those rules which speakers of the language use unconsciously.
Syntactical analysis of the sentences of natural language often requires reference to semantics, for without considering the meaning of a sentence it will be ambiguous. For example, let us take the sentence: ''Here are the lists of students that passed the physics exam. In this sentence the attribute ''that passed the physics exam'' refers to students. If we use parentheses to make the syntactical structure of the sentence more precise, as is done in writing algebraic and logical expressions, they would be placed as follows: ''Here are the lists of (students that . . . passed).'' Now let us take the following sentence: ''Here are the lists of students that were lying on the dean's shelf. Formally the structure of this sentence is exactly the same as in the preceding one. But in fact a different placement of parentheses is assumed here, specifically: ''Here are the (lists of students) that . . . were lying.'' When we arrange parentheses in this way mentally we are relying exclusively on the meaning of the sentence, for we assume that students could not be lying on the dean's shelf.
In general, constructions with the word ''that'' [Russian kotoryi] are very treacherous. In his book Slovo o slovakh [A Word about Words], L. Uspensky tells how he once saw the following announcement:
CITIZENS-TURN IN SCRAP MATERIAL TO THE YARDKEEPER THAT IS LYING AROUND!
It is not surprising that this construction did not find a place in mathematical logic!
THUS, to make a logical analysis-to construct the logical equivalent of a sentence in natural language. we must first of all make a syntactical analysis of the sentence; the results of the analysis will be reflected directly in the syntactical structure of the logical expression. But semantics is by no means left out either. When we say that "reddish-brown' is a one-place predicate, ''killed'' is a two-place predicate, ''distance'' is a function, ''and" is a logical connective, ''all'' is a quantifier, and so on, we are performing a semantic analysis of the concepts expressed in natural language. We classify concepts in accordance with a scheme fixed in the language of logic and we establish relations among the concepts. Logical analysis is essentially semantic analysis. Syntactical analysis is necessary to the extent that it is needed for semantic analysis.
Logical analysis may be more or less deep. In our example it is very superficial. Let us see if we could continue it. and if so how.
The concepts of ''dog," ''reddish-brown" and "cat'' are one place predicates, obviously elementary and not subject to further analysis. These are simple Aristotelian concepts which rely directly on sensory experience; every normal person is able to recognize them and the only way to explain what a ''cat'' is to point one out.
The concept ''stray'' is also a one-place predicate, although a more complex one. If we were reasoning in a formal grammatical manner we could conclude that "stray'' means "that which strays.'' But this would be an incorrect conclusion because the verb to stray does not designate a length of time. A perfectly well-bred house cat may go out for an hour and stray across a roof, but this does not give anyone the right to call it a ''stray.'' It would be more correct to define a stray cat as a cat that has no master or, using a relation which is already included in our logical expression, as a cat that does not belong to anyone. Here is a formal notation of this definition:
''stray'' (x) <=> - (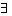
(It is assumed here that x is an arbitrary object.)
Let us look at the relation ''belongs.'' In a certain sense we sneaked it in because the word ''belong'' was not in the initial sentence. But it was understood and semantic analysis revealed it! In the Russian sentence the relation of belonging was conveyed by the genitive case. Here we see a clear example of the ambiguity and inadequacy of syntactical analysis. We used the genitive case in the constructions ''the widow's dog ''the dog of the widow''] and "the dog's mistress'' but in no way can it be said that the mistress belongs to her dog. The construction ''the widow's nose'' can of course be interpreted as the ''nose that belongs to the widow.'' But here we are already encountering the semantic ambiguity of the word ''belong,'' for it is obvious that the nose belongs to the widow in a different way than the dog belongs to her.
It requires a good deal of work to break the concept "belong" into its elementary constituent parts; this would require a description of the customs and laws related to the right of ownership. Only in this case can the meaning of ''belong'' be explained. The predicate "widow" and the functions "rank'' and ''surname'' (which we introduced during our analysis of the concept ''Lieutenant Pshebyssky'') are also bound up with the social sphere and require further analysis. Finally the concept "killed'' although it is not linked with the social sphere and is plainly simpler (closer to sensory experience) than the preceding concepts would also have to be subjected to logical analysis. In this analysis it would be possible to identify. first of all the element of completion in the action. which is expressed by the Russian verb form secondly the final result (the death of the victim) and thirdly the typical characteristic of the action expressed by the Russian verb zagryzt' ]-use of the teeth.
Logical analysis of language is an extremely interesting line of investigation, but we cannot dwell on it here. Those who are interested are referred to Elements of Symbolic Logic (New York: Free Press. 1966) by H. Reichenbach one of the founders of this field.
Let us summarize the results of our comparison between natural language and the language of logic. The language of logic has a simple and completely formalized syntax. By syntactical and semantic analysis a text in natural language can be translated to the language of logic-that is, it can be correlated with a text in the language of logic that has the same meaning. Semantic analysis of the natural text during translation may be more or less deep which is to say that the predicates and functions included in the logical text may be closer or further from immediate sensory and emotional experience. There are predicates and functions which cannot be broken down into more elementary constituents and which therefore cannot be defined in any way except by reference to experience. We shall call such predicates and functions primary.