Neutral selection plays an important role in the
evolution of populations, having a finite population size n [1]
. To demonstrate the neutral selection features
explicitly, let's consider the pure neutral evolution game, which
is defined as follows:
| ; |
1. There is a population of black and white balls,
the total number of the balls in a population is equal to
n . |
| ; |
2. The evolution consists of consequent generations.
Each generation consists of two steps. At the first step
we duplicate each ball, conserving its color: a black
ball has two black offsprings, a white ball has two white
ones. At the second step we randomly remove from a
population exactly half of the balls with equal
probability for black and white "species",
independently of their color. |
We say that the population is in l -state, if the
numbers of black and white balls at a considered generation are
equal to l and n-l, respectively. We can
characterize the evolution by the probability Plm
of a transition from l -state to m -state
during one generation. Using a straightforward combinatorial
consideration, we can calculate the values of Plm
:
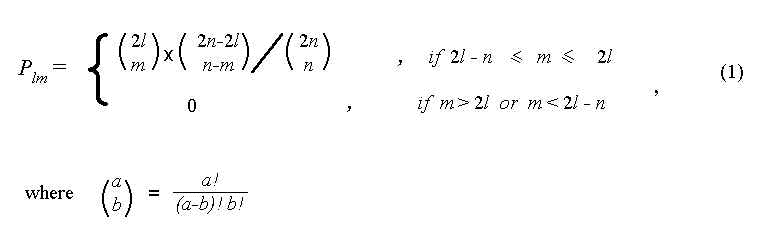
The matrix Plm determines the
random Markovian process, which can be considered as an example
of a simple stochastic genetic process [2]. Using the general
methods of analysis of such processes [2], we can deduce that:
1) the considered process always converges to one of two
absorbing states, namely, to 0-state (all balls are
white), either to n-state (all balls are
black);
2) at large n the characteristic number of
generations Tn , needed to converge
to the either absorbing state, is equal to 2n :
Thus, although this evolution is purely neutral (black and white
balls have equal chances to survive), nevertheless only one
species is selected. The value Tn characterizes
the neutral selection rate, it is used in our estimations (Quasispecies , Estimation
of the evolution rate).
References:
1. M. Kimura. "The neutral theory
of molecular evolution". Cambridge Un-ty Press. 1983.
2. S. Karlin. "A first course in
stochastic processes". Academic Press. New York, London,
1968.

