The basic evolutionary-systemic and constructive principles that have been discussed in my two previous contributions to this volume can be directly applied to the design of a computer support system that would help Principia Cybernetica collaborators to develop a coherent system of philosophical thought. In fact the same type of support system might be applied to any complex problem domains where on the basis of a lot of ill-structured, ambiguous and sometimes inconsistent data a more or less simple and reliable model is to be built. The problem we are speaking about is one of applied epistemology. A good epistemology, offering a concrete and general theory of how knowledge develops during individual or cultural evolution, should also be useful as a guide when a new model is practically to be developed.
Of course, these different concepts will be related and one chunk will in general contain references to several other chunks. For example, the chunk denoting the concept "dog" might contain the following sentence: a dog is a carnivorous mammal, with a protruding snout. This means that the concept dog has associations with a least the concepts mammal, carnivorous and snout. If these concepts are also available as chunks, then we might create a link from the dog chunk to the mammal chunk and so on. Computer applications that allow such an easy representation and manipulation of chunks connected by links are called hypermedia systems. The chunk with its text and graphics can be shown in a window on the screen, and it suffices to click on one of the links to show the next chunk to which the link is pointing (Heylighen, 1991).
Hypermedia system are useful for storing a large amount of complex, interrelated information (e.g. an encyclopedia) in a easy to handle way. However, there is an inherent ambiguity involved, since it is not a priori clear what a link is supposed to mean: any kind of association, as well causal, as logical, as intuitive as spatial, ..., might be represented by a link. Therefore we need a better structured system if we want our networks of concepts to support us more efficiently. By introducing different types of chunks (nodes) and links we may turn our hypermedia system into a semantic network: the different types of links will determine (part of) the meaning of the concept to which they are attached. The problem with semantic networks for knowledge representation is still that of ambiguity: there is an unlimited number of link and node types that may seem appropriate, and their interrelationships will in general be very unclear. In order to limit the set of types, we need an unambiguous, fundamental interpretation of what concepts and links in our network really stand for. I will now propose such an interpretation with the corresponding types, and show how it can be applied to the structuring of knowledge.
One way to define a concept is by listing the set of concepts that it entails together with the set of concepts entailed by it. By entailment I mean an "if...then" relation, which is more general than the logical (material) implication. For example, if a phenomenon is a dog, then it is also a mammal: dog -> mammal. It means that a phenomenon denoted by the first concept cannot be present or actual, without a phenomenon denoted by the second one being (simultaneously) or becoming (afterwards) actual.
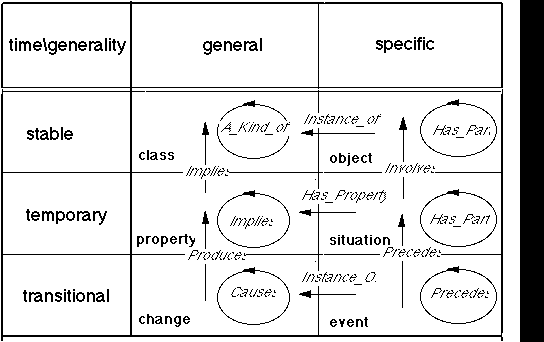
In order to derive fundamental types of distinctions (concepts, nodes) and links (entailments), we will posit two basic dimensions of distinction: stability (or time) and generality, with the corresponding values of instantaneous - temporary - stable, and of specific - general. The combination of these 3 x 2 values leads to 6 types of distinction (see table).
time\generality general specific
stable class object
temporary property situation
instantaneous change event
For example, an object is a distinction that is stable (it is not supposed to appear or disappear while we are considering it), and specific (it is concrete, there is only of it). A property is a distinction that is general (several phenomena may be denoted by it, it represents a common feature), and temporary (it may appear or disappear, but normally it remains present during a finite time interval). An event is instantaneous (it appears and disappears within one moment), and specific (it does not denote a class of similar phenomena, but a particular instance).
With these node types we can now derive the corresponding link types by considering all possible combinations of two node types. There is one constraint, however: we assume that a more invariant (stable or general) distinction can never entail a less invariant one. Otherwise, the second would be present each type the first one is, contradicting the hypothesis that it is less invariant than the first one. For example, a class cannot entail an object, a situation cannot entail an event. Yet it is possible that concepts with the same type of invariance, (e.g. two objects) might be connected by an entailment relation. All remaining possible combinations can now be summarized by the following scheme (the straight arrows represent entailment from one type to another (more invariant) one, the circular arrows entailment from a concept of a type to a concept of the same type):

For example when an object A entails a class B, A -> B, then A is an Instance_of B. When an object A always entails the presence of another object B, then B must belong to or be a part of A. When a change A entails another change B, then A and B "covary" and hence A can be interpreted as the cause of B. When an event A entails a situation B, then A must be simultaneous with or preceding B in time.
The advantage of this scheme is that most of the intuitive and often used semantic categories (objects, classes, causality, whole-part relations, temporal precedence, etc.) can be directly constructed from it, in a simple and uniform format. Complementarily, given some of those everyday categories, we can use the scheme to reduce them to simple entailment links between nodes of specific types. In fact the types themselves can be represented as nodes, and each node of a particular type will have an entailment link to that 'type'-node. This allows us to reduce a complicated set of semantic categories to an extremely simple formal strcuture.
Input: I(x) = { y | y -> x} = "extension" of concept x
Output : O(x) = { y | x -> y } = "intension" of concept x
The meaning (definition, distinction) of x can be interpreted as determined by the disjunction of its input elements, and the conjunction of its output elements. Our previous remark about definitions can now be reformulated as the following bootstrapping axiom (Heylighen, 1990ab):
two nodes are distinct if and only if their input and output sets are distinct:
x != y <=> I(x) != I (y), O(x) != O(y)
("!=" stands here for "is not equal to")
However, such a complete definition assumes that all concepts allowing to distinguish between x and y are present in the network. In practice, the network of concepts we are building by writing down our knowledge in the form of connected chunks, will be incomplete in some respects, redundant in other respects. Instead of using the axiom as a static description of how a complete network should be structured, we can use it as a procedure to find ways to make the network more adequate, by adding missing concepts, or by deleting redundant ones. We can distinguish the following two main techniques (cf. Heylighen, 1991; Bakker, 1987; Stokman & de Vries, 1988):
1) I (x) = I (y):
a) O (x) = O (y) => Identify (or distinguish) x and y
b) O (x) c O (y) => Identify x and y, or distinguish I (x) from I (y)
2) I(x) c I(y):
a) O(x) = O(y) => Identify x and y, or distinguish O(x) from O(y)
b) O(x) c O(y) => Identify x and y
c) O(y) c O(x) => Connect x to y, x -> y
(" c " stands here for "subset of")
From that point of view, the cluster may be called closed (Heylighen, 1990a) and it might therefore be replaced by a single "integrated" node. The integrated node "summarizes" the cluster nodes on a more abstract level, and may hence simplify the conceptual model. Similar to the case of node identification, the external indistinguishability of clustered nodes may be spurious, and this should prompt the user to add additional distinguishing links and nodes.
There are different types of closure, with different meanings and formal properties, depending upon which sets of external input or output nodes are common among the cluster, for example: transitive closure, equivalence, cyclical closure, ... If the closure is only approximative (the cluster nodes have several external neighbours in common, but these do not form a complete set of any specific type), then this method is similar to the one called "conceptual clustering" in machine learning, where the boundaries between clustered and non-clustered nodes become fuzzy, and depend on the treshold chosen for the number of common neighbours.
In conclusion, the present set of concepts and techniques, when implemented on a computer through a suitable intuitive interface, should enable an individual or group of users to elicit and structure their knowledge about a domain under the form of a network of concepts connected by entailment links, and support them to minimize the redundancy, complexity and incompleteness of their model.
The introduction of new nodes and links by the user corresponds to a form of variation by recombination of concepts. The recognition of a closed cluster of nodes by the system corresponds to the selection of a distinction that is more stable or invariant than the distinctions between the internal concepts of the cluster (Heylighen, 1990a), with closure as fundamental selection criterion. The elicitation and structuring of concepts in this manner hence follows the general evolutionary mechanism that was postulated in my previous papers about evolutionary philosophy.
References
Bakker R.R. (1987): Knowledge Graphs: representation and structuring of scientific knowledge, (Ph.D. Thesis, Dep. of Applied Mathematics, University of Twente, Netherlands).
Heylighen F. (1990): "A Structural Language for the Foundations of Physics", International Journal of General Systems 18, p. 93-112 .
Heylighen F. (1990): "Relational Closure: a mathematical concept for distinction-making and complexity analysis", in: Cybernetics and Systems '90, R. Trappl (ed.), (World Science, Singapore), p. 335-342.
Heylighen F. (1991): "Design of a Hypermedia Interface Translating between Associative and Formal Representations", International Journal of Man-Machine Studies.
Stokman F.N. & de Vries P.H. (1988): "Structuring Knowledge in a Graph", in: Human-Computer Interaction, Psychonomic Aspects, G.C. van der Veer & G.J. Mulder (eds.), (Springer, Berlin).