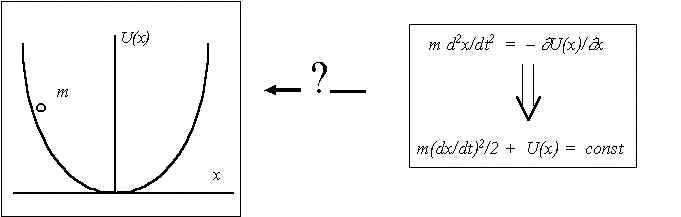
This paper was published in Proceedings of The Second International Symposium on Neuroinformatics and Neurocomputers, Rostov-on-Don, 1995. PP. 422-429.
Towards the evolutionary biocybernetics
V.G.Red'ko
Research and Development Institute of Material Science
Zelenograd, Moscow 103460, Russia
1. Intellectual inventions of biological evolution
It is interesting to understand how did a human logic through the biological evolution arise. This question correlates with a profound gnosiological problem: why is a human logic applicable to a cognition of the nature? Let's illustrate this problem by simple example.
Let's suppose that physicist has described some phenomenon by means of differential equation (Fig.1). Then he integrates the equation and obtains the phenomenon characteristics. The transition from equation to characteristics is purely deductive, but applicability of this transition to physical phenomenon should be proved because it is not evident that physical objects obey the human logic rules.
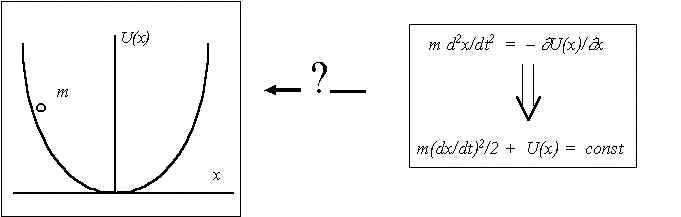
Fig.1. Why is human deduction applicable to natural phenomena?
In order to understand, why and how did logic rules and their applicability to the nature cognition arise, it is reasonable to construct the theory of evolutionary origin of human logic. Such a theory could include the mathematical models of the most important "intellectual inventions" of biological evolution (fig.2) [1] by means of which animals "cognize" the natural regularities as well as the models of evolutionary transitions between intellectual inventions of different levels.
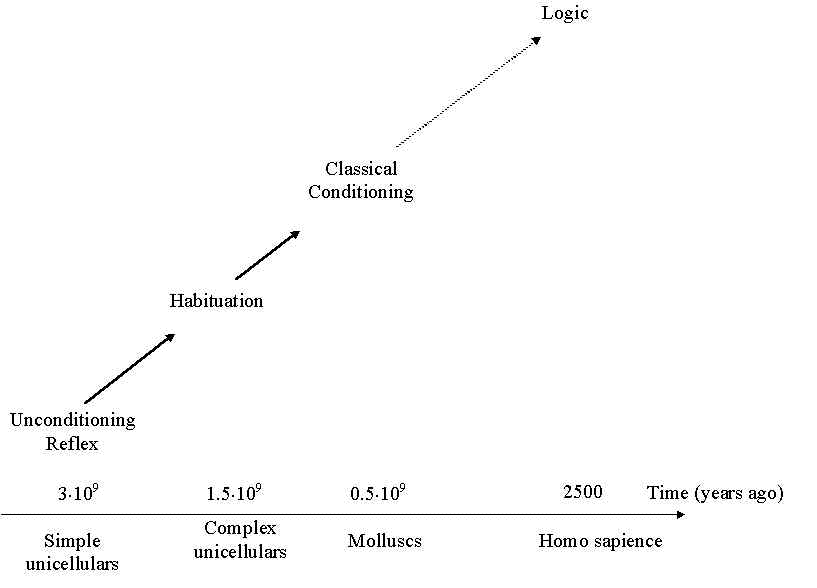
Fig.2. Intellectual inventions of biological evolution. "Authors of inventions and priorities dates" are shown drafty.
2. Evolutionary biocybernetics - the scope of the science
In my opinion, the logic origin theory should be an important part of evolutionary biocybernetics. Fig.3 illustrates the branches of the researches that can be referred to the evolutionary biocybernetics.
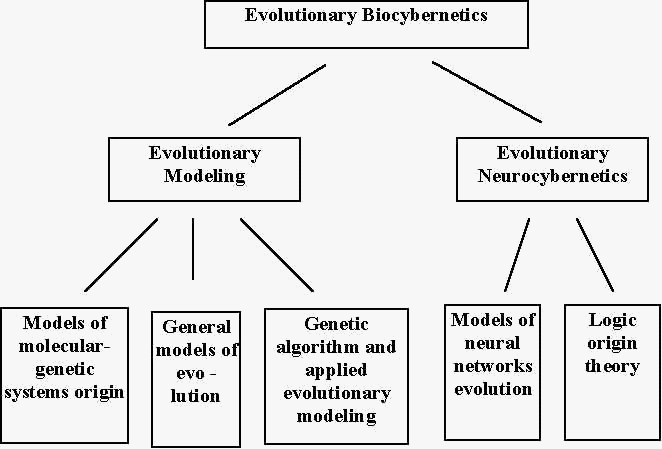
Fig.3. The research branches of the evolutionary biocybernetics.
For the sake of the briefness, I shall mention only a few examples of the researches represented by fig.3.
Models of molecular-genetic systems origin have been constructed in connection with the life origin problem. Quasi-species [2], hypercycles [3], and sysers [4] are the most known; these models describe mathematically some hypothetical processes of the evolutionary origin of cybernetic properties of primitive organisms.
General models of evolution describe some informational and cybernetic aspects of evolution. Kauffman's automata [5] is an interesting example of them. These models describe dynamics of the systems of randomly coupled logical elements. Kauffman's automata can be interpreted as models of cellular molecular-genetic control systems. Effective methods of statistical physics are used to study the evolution of these automata [6].
In genetic algorithm and applied evolutionary modeling the symbol strings (model "genomes") are optimized according to some quality function ("organisms fitnesses") through the mutations, crossovers, and selection of the strings [7-9]. The combinatorial optimization is under particular interest of applied evolutionary modeling.
Several models of neural networks evolution appeared last years [10,11]; they describe the optimization of structure or parameters of neural networks by means of genetic or evolutionary algorithms.
The logic origin theory is not yet developed, and approaches to its construction will be discussed in the next section.
3. Logic origin theory - backgrounds and approaches
3.1. Logic origin theory and mathematical logic. Mathematical logic gives the answers to the questions: "How are the human logic rules?", and "How may logic rules be used correctly?". Logic origin theory could give answers to more deep questions: "Why are the human logic rules such as they are?", and "Why can logic rules be used correctly?"
3.2. Logic origin theory and artificial intelligence. While constructing artificial intelligence systems it is desirable to know, what are application areas of the certain "intellectual" method, and what is the cause of biological origin of this method. Such an understanding could be obtained in logic origin theory investigations.
3.3. Logic origin theory and neural networks. In my opinion, the relation between logic origin theory and neural network theory should be analogous to that of between thermodynamics and statistical mechanics: the scope of logic origin theory is phenomenological investigations of "intellectual" methods, rules, and phenomena; the scope of neural network theory is researches of corresponding "microscopic" neural mechanisms.
3.4. Some steps towards logic origin theory. Let's note some model that could be included into future logic origin theory.
Adaptive syser [12] is the model of unconditional reflex at molecular-genetic level.
Tsetlin's automata [13] are significant models of adaptive behavior in changing external environment. Tsetlin's automata illustrate the simple acquired properties of biological organisms. The "intelligence level" of these automata corresponds approximately to that of habituation (fig.2).
There is a number of conditional reflex models, see for example [14-16]. But, in may opinion, some significant aspects of conditional reflex are not yet mathematically described, particularly it concerns to the role of the motivation in conditional learning.
The motivation (i.e. aspiration to reach a certain purpose) is an important property of "intelligent" animal behavior. It is included as significant participant in functional system of higher nervous activity by P.K.Anokhin [17]. The motivation is closely correlated with phenomenon of dominanta by A.A.Ukhtomsky [18]. The approaches to mathematical theory of dominanta have been developed by V.I.Kryukov [19]. A concept of purposeful action (that is similar to motivation) in connection with information theory development has been intensively discussed by V.I.Korogodin [20]. The motivation and its role in very primitive animal behavior have been modeled by L.E.Tsitolovsky et.al. [21]. In artificial intelligence investigations the models involving motivation have been also developed [16,22,23].
It is too early to speak about results of logic origin theory, but some analogies between "intellectual inventions" of different levels can be noted. For example, classical conditioning can be considered as elementary inference: "If conditioned stimulus is followed by unconditioned stimulus and unconditioned stimulus is followed by certain animal reaction, then conditioned stimulus is followed by the same reaction", that represents the early ancestor of important deductive formula:
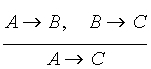
(if A implies B and B implies C, then A implies C).
4. Concluding remarks
The preceding consideration of evolutionary biocybernetics is not complete: there are several potential branches of researches, which could be included in scheme of fig. 3. For example, evolution of sensory systems and evolution of internal homeostasis control systems could be interesting subjects of investigation. But logic origin theory is the most fundamental among them.
Finally, it should to emphasize that logic origin theory is very interesting and perspective field of theoretical investigations, and aspiration to understand the causes of human logic cognition abilities could be a guide star of these investigations.
References
1. Voronin L.G. Evolution of higher nervous activity. Moscow: Nauka, 1977. 128 p. (In Russian).
2. Eigen M., McCasill J., Schuster P. Molecular quasi-species. // Journal of Physical Chemistry. 1988. Vol.92. N.24. PP.6881-6891.
3. Eigen M., P.Schuster P. The hypercycle: A principle of natural self-organization. Springer Verlag: Berlin etc. 1979. 92p.
4. Ratner V.A., Shamin V.V. Sysers: modeling of fundamental features of molecular-biological organization. Matching between the general properties of genetic processes and structural peculiarities of macromolecular assemblies. // Zhurnal Obshchei Biologii. 1983. Vol.44. N.1. PP. 51-61 (In Russian).
5. Kauffman S.A., Smith R.G. Adaptive automata based on Darwinian selection. // Physica D. 1986. Vol.22. N.1-3. PP.68-82.
6. Weinberger E.D. Local properties of Kauffman's N-k model: A tunably rugged energy landscape. // Physical Review. 1991. Vol.44. N.10. PP.6399-6413.
7. Fogel L.J., Owens A.J. Walsh M.J. Artificial intelligence through simulated evolution. Wiley. New York, 1966.
8. Holland J.H. Adaptation in natural and artificial systems. Un-ty of Michigan Press. Ann Arbor, 1975.
9. Bukatova I.L. Evolutionary modeling and its applications. Moscow: Nauka, 1979. 231 p. (In Russian).
10. Mangel M. Evolutionary optimization and neural networks models of behavior. // J. of Math. Biol. 1990. Vol.28. PP.237-256.
11. Teriokhin A.T., Budilova E.V. On evolutionary optimal neural networks controlling diurnal vertical migration in zooplancton. // J. Modeling, Measurement, and Control. Series C. 1996. Vol.55. N.1. PP.7-11.
12. Red'ko V.G. Adaptive syser. // Biofizika. 1990. Vol. 35. N.6. PP. 1007-1011 (In Russian).
13. Tsetlin M.L. Investigations on the automata theory and modeling of biological systems. Moscow: Nauka, 1969. 316 p. (In Russian).
14. Grossberg S. Classical and instrumental learning by neural networks. // Progress in Theoretical Biology. 1974. Vol.3. PP.51-141.
15. Barto A.G., Sutton R.S. Simulation of anticipatory responses in classical conditioning by neuron-like adaptive element. // Behav. Brain Res. 1982. Vol.4. P.221.
16. Gaase-Rapoport M.G., Pospelov D.A. From amoeba to robot: models of behavior. Moscow: Nauka, 1987. 288 p. (In Russian).
17. Anokhin P.K. System mechanisms of higher nervous activity. Moscow: Nauka, 1979. 453 p. (In Russian).
18. Ukhtomsky A.A. Dominanta as factor of behavior. // Collected works. Leningrad, 1950. Vol.1. PP.293-315. (In Russian).
19. Kryukov V.I. An attention model based on the principle of dominanta. // Proceedings in Nonlinear Science. Neurocomputers and Attention I: Neurobiology, Synchronization and Chaos. 1989. Ed. by A.Y.Holden and V.I.Kryukov. PP.319-351.
20. Korogodin V.I. Information and the phenomenon of life. Pushchino, 1991. 202 p. (In Russian).
21. Tsitolovsky L.E. Private communication.
22. Modeling of learning and behavior. Moscow: Nauka, 1975. (In Russian).
23.Weinzweig M.N., Polyakova M.P. Architecture of thinking system and neural networks. // Intelligence Processes and Their Modeling. Informational networks. Moscow, 1994. PP.132-151. (In Russian).