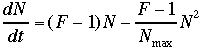The overall survival and proliferation rate of a meme m can be expressed as the meme fitness F(m), which measures the average number of memes at moment t divided by the average number of memes at the previous time step or "generation" t - 1. This fitness can be expressed in a simplified model as the product of the fitnesses or survival rates for each of the four stages of the meme life-cycle, respectively assimilation A, retention R, expression E and transmission T:
F(m) = A(m) . R(m) . E(m) . T(m)
A denotes the proportion of memes vehicles encountered (or memes independently discovered) by the host that are assimilated. R represents the proportion of these assimilated memes that are retained in memory. Therefore, A ≤ 1, R ≤ 1. E is the number of times a retained meme is expressed by the host. T is the number of potential new hosts that is reached by the expression. (T could be estimated more accurately as the number of copies made of the expression times the duration during which each copy survives times the number of people subjected to a copy per time unit). Unlike A and R, E and T do not have an upper bound, although E is likely to be more restricted than T. Note that F is zero as soon as one of its components (A, R, E, T) is zero. This expresses the fact that a meme must successfully pass through all four stages in order to replicate. Also note that for a meme to spread (F > 1), you must have at least E > 1 or T > 1.
Which memes will most successfully pass all these stages can be modelled by a series of selection criteria. At present, we have no method to derive the value of the fitness components from the degree to which a meme fulfils the different criteria. This does not mean that no predictions can be made, though. All other things being equal, a meme that scores better on one of these criteria is predicted to become more numerous in the population than a meme that scores worse. This is a falsifiable hypothesis, which can be tested through experiments or observations. For that, it suffices to operationalize the tested criterion.
Population Growth
Assuming that we would know the value of F(m), we can in principle calculate the number of hosts of the meme m at a given moment t, by using a general  model of population growth. In this model, we assume that a population N(t) of hosts first grows exponentially, because the number of newly infected hosts at each time step or "generation" is proportional to the number of hosts that are already infected. But a meme can never infect more individuals than the maximum number of potential hosts: Nmax. Therefore, the exponential growth slows down until it reaches the maximum, resulting in the well-known logistic or "S-shaped" curve.
model of population growth. In this model, we assume that a population N(t) of hosts first grows exponentially, because the number of newly infected hosts at each time step or "generation" is proportional to the number of hosts that are already infected. But a meme can never infect more individuals than the maximum number of potential hosts: Nmax. Therefore, the exponential growth slows down until it reaches the maximum, resulting in the well-known logistic or "S-shaped" curve.