|
Fitness Landscapes
In many cases, the rather abstract and mathematically complex structure
of a system of attractors and basins can be replaced by the more intuitive
model of a fitness landscape. Under certain mathematical conditions, the
deterministic dynamics of a system can be represented by a potential
function F on the state space, which attaches a certain number to each
state: F: S -> R: s -> F(s),
such that trajectory of the system through the state space will always follow
the path of steepest descent, i.e. move from a given state s to that
neighboring state for which F is minimal. In mechanics, this function
corresponds to the potential energy of the system. More generally, the function
represents the degree to which a certain state is "preferable" to another
state: the lower the value of F, the "better" or the more "fit" the
state. Thus, the potential can be seen as the negative of the fitness function.
It is unfortunate that the convention in physics sees systems as striving to
minimize a potential function, whereas the convention in biology sees systems
as striving to maximize a fitness function. Although this tends to be
confusing, the two types of representation are equivalent apart from an
inversion of the sign of the function.
The fitness function transforms the state space into a fitness
landscape, where every point in the space has a certain "height"
corresponding to its fitness value. This landscape has peaks and valleys. The
attractors of the dynamics will now correspond to the local minima of the
potential function (potential valleys), or, equivalently, to the maxima of the
fitness function (fitness peaks). This can be understood by noting that the
system will always move downward in the potential landscape. When it has
reached the locally lowest point, all remaining directions will point upward,
and therefore the system will not be able to leave the bottom of the valley
(see figure).
The local maxima of the potential (peaks) are the points that separate the
basins of the attractors (valleys) that lie in between the peaks. In general,
the steeper the slope, the faster the descent of the system along that slope.
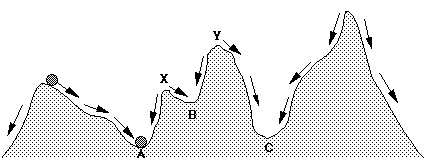
Figure: a fitness landscape: the arrows denote the directions in
which the system will move. The height of a position corresponds to its
potential or to its lack of fitness. Thus, A has a higher fitness (or lower
potential) than B. The bottoms of the valleys A, B and C are local minima of
the potential, i.e. attractors. The peaks X and Y delimit the basin of the
attractor B. X separates the basins of A and B, Y separates the basins of B and
C.
Copyright© 1999 Principia Cybernetica -
Referencing this page
|
|
|

