Entropy (or uncertainty) and its complement, information, are perhaps the most fundamental quantitive measures in cybernetics, extending the more qualitative concepts of variety and constraint to the probabilistic domain.
Variety and constraint, the basic concepts of cybernetics, can be measured in a more general form by introducing probabilities. Assume that we do not know the precise state s of a system, but only the probability distribution P(s) that the system would be in state s. Variety V can then be expressed as entropy H (as originally defined by Boltzmann for statistical mechanics):
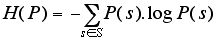
H reaches its maximum value if all states are equiprobable, that is, if we have no indication whatsoever to assume that one state is more probable than another state. Thus it is natural that in this case entropy H reduces to variety V. Like variety, H expresses our uncertainty or ignorance about the system's state. It is clear that H = 0, if and only if the probability of a certain state is 1 (and of all other states 0). In that case we have maximal certainty or complete information about what state the system is in.
We define constraint as that which reduces uncertainty, that is, the difference between maximal and actual uncertainty. This difference can also be interpreted in a different way, as information, and historically H was introduced by Shannon as a measure of the capacity for information transmission of a communication channel. Indeed, if we get some information about the state of the system (e.g. through observation), then this will reduce our uncertainty about the system's state, by excluding--or reducing the probability of--a number of states. The information I we receive from an observation is equal to the degree to which uncertainty is reduced:
I = H(before) - H(after)
If the observation completely determines the state of the system (H(after) = 0), then information I reduces to the initial entropy or uncertainty H.
Although Shannon came to disavow the use of the term "information" to describe this measure, because it is purely syntactic and ignores the meaning of the signal, his theory came to be known as Information Theory nonetheless. H has been vigorously pursued as a measure for a number of higher-order relational concepts, including complexity and organization. Entropies, correlates to entropies, and correlates to such important results as Shannon's 10th Theorem and the Second Law of Thermodynamics have been sought in biology, ecology, psychology, sociology, and economics.
We also note that there are other methods of weighting the state of a system which do not adhere to probability theory's additivity condition that the sum of the probabilities must be 1. These methods, involving concepts from fuzzy systems theory and possibility theory, lead to alternative information theories. Together with probability theory these are called Generalized Information Theory (GIT). While GIT methods are under development, the probabilistic approach to information theory still dominates applications.
Reference:
Heylighen F. & Joslyn C. (2001): "Cybernetics and Second Order Cybernetics", in: R.A. Meyers (ed.), Encyclopedia of Physical Science & Technology , Vol. 4 (3rd ed.), (Academic Press, New York), p. 155-170

